La notation décimale est une façon d’écrire les nombres réels où une partie entière et une partie décimale sont séparées par une virgule.

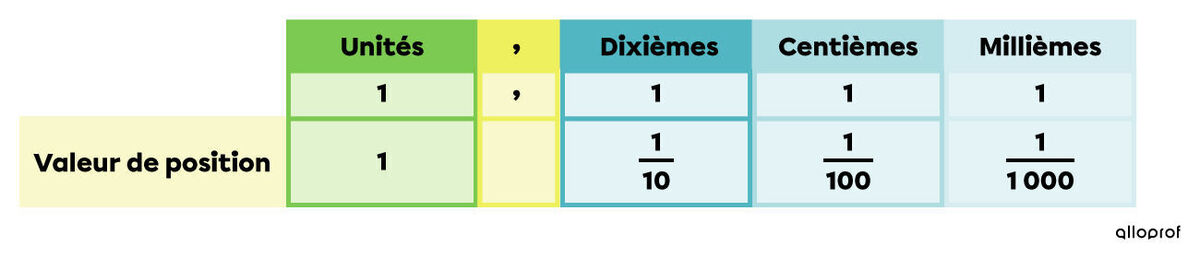
Dans un nombre écrit en notation décimale, chaque chiffre occupe une position reliée à une valeur précise. C’est ce qu’on appelle la valeur de position.
La partie entière comprend les chiffres à gauche de la virgule, soit les unités, les dizaines, les centaines, etc. La partie décimale comprend les chiffres à droite de la virgule, soit les dixièmes |\left(\dfrac{1}{10}\right)\!,| les centièmes|\left(\dfrac{1}{100}\right)\!,| les millièmes |\left(\dfrac{1}{1\ 000}\right)\!,| etc.
Remarque : La partie décimale d’un nombre est parfois appelée partie fractionnaire, car elle fait justement référence à des fractions.
Il ne faut pas confondre le concept de la notation décimale avec celui d’un nombre décimal.
-
La notation décimale est une façon d’écrire les nombres.
-
Un nombre décimal est une catégorie de nombres.
Voici un exemple d’utilisation de la notation décimale pour chacune des catégories de nombres suivants.
Les nombres décimaux ||1{,}4||
Les nombres périodiques ||2{,}\overline{5}||
Les nombres irrationnels ||\pi=3{,}141\,592\,654…||
Un nombre décimal est un nombre rationnel dont la partie décimale est composée d’une quantité finie de chiffres.
L’ensemble des nombres décimaux est représenté par le symbole |\mathbb{D}.| Les nombres décimaux font partie des nombres rationnels.

Si une fraction d’entiers donnée est équivalente à une fraction dont le dénominateur est une puissance de |10,| alors cette fraction représente un nombre décimal, sinon c’est un nombre périodique.
Nombres décimaux
-
|\dfrac{1}{\bf{2}}\begin{align}\times\,\color{#3a9a38}{\bf{5}}\\[-1pt] \times\,\color{#3a9a38}{\bf{5}}\end{align}= \dfrac{5}{10}=0{,}5|
-
|\dfrac{3}{\bf{5}}\begin{align}\times\,\color{#3a9a38}{\bf{2}}\\[-1pt] \times\,\color{#3a9a38}{\bf{2}}\end{align}= \dfrac{6}{10}=0{,}6|
-
|\dfrac{14}{20}\begin{align}\div\,\color{#3a9a38}{\bf{2}}\\[-1pt] \div\,\color{#3a9a38}{\bf{2}}\end{align}= \dfrac{7}{10}=0{,}7|
-
|\dfrac{3}{4}\begin{align}\times\,\color{#3a9a38}{\bf{25}}\\[-1pt] \times\,\color{#3a9a38}{\bf{25}}\end{align}= \dfrac{75}{100}=0{,}75|
-
|\dfrac{12}{25}\begin{align}\times\,\color{#3a9a38}{\bf{4}}\\[-1pt] \times\,\color{#3a9a38}{\bf{4}}\end{align}= \dfrac{48}{100}=0{,}48|
-
|\dfrac{7}{8}\begin{align}\times\,\color{#3a9a38}{\bf{125}}\\[-1pt] \times\,\color{#3a9a38}{\bf{125}}\end{align}= \dfrac{875}{1\,000}=0{,}875|
-
|\dfrac{3}{6}\begin{aligned}\div\,\color{#3a9a38}{\bf{3}}\\[-1pt] \div\,\color{#3a9a38}{\bf{3}}\end{aligned}= \dfrac{1}{\bf{2}}\begin{aligned}\times\,\color{#3a9a38}{\bf{5}}\\[-1pt] \times\,\color{#3a9a38}{\bf{5}}\end{aligned}= \dfrac{5}{10}=0{,}5|
Nombres périodiques
-
|\dfrac{1}{\bf{3}}\begin{align}\times\,\color{#ec0000}{\bf{?}}\\[-1pt] \times\,\color{#ec0000}{\bf{?}}\end{align}=\, \dfrac{\color{#ec0000}{\bf{?}}}{10...}|
Il n’existe pas de nombre entier qui permet de transformer |\dfrac{1}{3}| en une fraction sur |10| ni sur aucune autre puissance de |10.| Par conséquent, |\dfrac{1}{3}| ne représente pas un nombre décimal, mais un nombre périodique.
|\dfrac{1}{3} =0{,}333\,333...=0{,}\overline{3}| -
|\begin{align}\dfrac{2}{\bf{7}}\begin{aligned}\times\,\color{#ec0000}{\bf{?}}\\[-1pt] \times\,\color{#ec0000}{\bf{?}}\end{aligned}&=\ \dfrac{\color{#ec0000}{\bf{?}}}{10...}\\[6pt] \dfrac{2}{7} &=0{,}285\,714\,285...=0{,}\overline{285\,714} \end{align}|
-
|\begin{align}\dfrac{4}{9}\begin{aligned}\times\,\color{#ec0000}{\bf{?}}\\[-1pt] \times\,\color{#ec0000}{\bf{?}}\end{aligned}&=\ \dfrac{\color{#ec0000}{\bf{?}}}{10...}\\[6pt] \dfrac{4}{9} &=0{,}444...=0{,}\overline{4} \end{align}|
-
|\begin{align}\dfrac{4}{6}\begin{aligned}\,\div\ \,\color{#3a9a38}{\bf{2}}\\[-1pt] \div\ \,\color{#3a9a38}{\bf{2}}\end{aligned}&=\ \dfrac{2}{\bf{3}}\begin{aligned}\times\,\color{#ec0000}{\bf{?}}\\[-1pt] \times\,\color{#ec0000}{\bf{?}}\end{aligned}\, =\,\dfrac{\color{#ec0000}{\bf{?}}}{10...}\\[6pt] \dfrac{4}{6}=\dfrac{2}{3}&=0{,}666...=0{,}\overline{6}\end{align}|
Un nombre périodique est un nombre rationnel dont la partie décimale est composée d’une séquence de chiffres qui se répète.
La période est la séquence qui se répète.
Pour indiquer qu’un nombre est périodique, on trace un trait au-dessus de la séquence qui se répète (la période).
|\dfrac{4}{3}=1{,}333\,333...=1{,}\overline{3}|
La période est |3.|
|\dfrac{35}{11}=3{,}181\,818\,181...=3{,}\overline{18}|
La période est |18.|
Ce n’est pas toujours toute la partie décimale d’un nombre qui se répète.
|\dfrac{38}{15}=2{,}533\,333...=2{,}5\overline{3}|
La période est |3| seulement. Le chiffre |5| ne se répète pas.
|\dfrac{41}{12}=3{,}416\,666\,666...=3{,}41\overline{6}|
La période est |6| seulement. Les chiffres |4| et |1| ne se répètent pas.
La calculatrice peut parfois nous induire en erreur. Beaucoup de modèles arrondissent le dernier chiffre affiché de la partie décimale, ce qui peut nous porter à croire que le nombre n’est pas périodique, alors que c’en est bel et bien un.
Par exemple, pour connaitre la notation décimale équivalente à la fraction |\dfrac{2}{3},| il faut diviser |2| par |3.| La plupart des calculatrices affichent |0{,}666\,666\,667.| Pourtant, tous les nombres rationnels, soit ceux qui peuvent s’écrire sous la forme d’une fraction d’entiers, sont périodiques. ||\dfrac{2}{3}=0{,}666\,666…=0{,}\overline{6}||

Un nombre irrationnel est un nombre dont la partie décimale est composée d’une quantité infinie de chiffres sans répétition.
|\sqrt{2},| écrit en notation décimale est : |1{,}414\,213\,562…|
Bien qu’il soit possible d’écrire une approximation du nombre |\sqrt{2}| en utilisant la notation décimale, ce dernier n’est pas un nombre décimal, puisque la partie décimale ne compte pas un nombre fini de chiffres. Il ne s’agit pas non plus d’un nombre périodique, car il ne présente pas de séquence de chiffres qui se répète indéfiniment. |\sqrt{2}| est donc un nombre irrationnel.
Voici d’autres exemples de nombres irrationnels avec leur représentation en notation décimale.
|\begin{align}\dfrac{\sqrt{5}}{2}&=1{,}118\,033\,989…\\\\ \pi&=3{,}141\,592\,654…\end{align}|
Le nombre d’or : |\varphi=1{,}618\,033\,989…|
Les racines ne sont pas nécessairement des nombres irrationnels. Il peut s’agir de nombres entiers ou de nombres décimaux.
-
|\sqrt{9}=3| est un nombre entier.
-
|\sqrt{12{,}96}=3{,}6| est un nombre décimal.