We can sub-classify natural numbers |(\mathbb{N})| according to certain characteristics.
An even number is an integer that is divisible by |2.|
An even number is a quantity that can be divided into groups of |2| units without having a remainder. In other words, an even number can be defined as an integer divisible by |2| whose answer to the division is also an integer. (e.g. |6,\div 2 = 3|).
|4| sets of |2| units can be made from the number |8,| with no remainder.
Furthermore, note that the number |8| is divisible by |2.| ||8\div 2=4||
This means that |8| is an even number.
Even numbers can be recognized by the digit in the ones position. Specifically, an even number can only end in the following digits:||0,2,4,6,8||
The following numbers are even numbers because they end with one of the 5 possible digits in the ones position.||2\ 00\boldsymbol{\color{#333fb1}{0}},10\boldsymbol{\color{#333fb1}{4}},\boldsymbol{\color{#333fb1}{4}},3\boldsymbol{\color{#333fb1}{2}},6\boldsymbol{\color{#333fb1}{6}},19\boldsymbol{\color{#333fb1}{8}},700\ 00\boldsymbol{\color{#333fb1}{0}}||
An odd number is an integer that is not divisible by |2.|
An odd number is a quantity that cannot be grouped into sets of |2| without creating a remainder. Dividing an odd number by |2| gives a fraction or decimal number as the answer.
Sets of |2| cannot be made from the number |7| without producing a remainder. There will be |3| sets of |2| units and a remainder of one unit.
Odd numbers can be recognized by looking at the digit in the ones position. Specifically, odd numbers can only end in the following digits:||1,3,5,7,9||
The following numbers are odd numbers because they end with one of the 5 possible digits in the ones position.||10\boldsymbol{\color{#3a9a38}{5}},5\boldsymbol{\color{#3a9a38}{3}},1\boldsymbol{\color{#3a9a38}{7}},\boldsymbol{\color{#3a9a38}{9}},2\boldsymbol{\color{#3a9a38}{1}},5\boldsymbol{\color{#3a9a38}{9}},10\boldsymbol{\color{#3a9a38}{3}},98\ 00\boldsymbol{\color{#3a9a38}{7}}||
A prime number is a natural number that has only 2 positive divisors, |1| and itself.
The number 0
The number |0| has an infinite number of divisors.||\begin{align}0\div1&=0\\0\div2&=0\\0\div3&=0\\&\ldots \end{align}||However, the number |0| cannot be divided by itself because dividing by |0| is an undefined operation. Therefore, it is not a prime number.
The number 1
The number |1| is not considered a prime number because it does not have 2 different divisors. It only has |1| as a divisor.
Example 1
Is the number |11| a prime number?
The only 2 numbers that |11| can be divided by without a remainder are |1| and |11.| Therefore, |11| is a prime number.
Example 2
Is the number |29| a prime number?
The only 2 numbers that |29| can be divided by without a remainder are |1| and |29.| Therefore, |29| is a prime number.
Example 3
Is the number |49| a prime number?
|49| is divisible by |1,| |7| and |49.| Since it has three different divisors, |49| is not a prime number. Instead, |49| is a composite number.
From the definition, we can create a list of the prime numbers in our number system.
| List of prime numbers less than |1000| | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| |2| | |3| | |5| | |7| | |11| | |13| | |17| | |19| | |23| | |29| |
| |31| | |37| | |41| | |43| | |47| | |53| | |59| | |61| | |67| | |71| |
| |73| | |79| | |83| | |89| | |97| | |101| | |103| | |107| | |109| | |113| |
| |127| | |131| | |137| | |139| | |149| | |151| | |157| | |163| | |167| | |173| |
| |179| | |181| | |191| | |193| | |197| | |199| | |211| | |223| | |227| | |229| |
| |233| | |239| | |241| | |251| | |257| | |263| | |269| | |271| | |277| | |281| |
| |283| | |293| | |307| | |311| | |313| | |317| | |331| | |337| | |347| | |349| |
| |353| | |359| | |367| | |373| | |379| | |383| | |389| | |397| | |401| | |409| |
| |419| | |421| | |431| | |433| | |439| | |443| | |449| | |457| | |461| | |463| |
| |467| | |479| | |487| | |491| | |499| | |503| | |509| | |521| | |523| | |541| |
| |547| | |557| | |563| | |569| | |571| | |577| | |587| | |593| | |599| | |601| |
| |607| | |613| | |617| | |619| | |631| | |641| | |643| | |647| | |653| | |659| |
| |661| | |673| | |677| | |683| | |691| | |701| | |709| | |719| | |727| | |733| |
| |739| | |743| | |751| | |757| | |761| | |769| | |773| | |787| | |797| | |809| |
| |811| | |821| | |823| | |827| | |829| | |839| | |853| | |857| | |859| | |863| |
| |877| | |881| | |883| | |887| | |907| | |911| | |919| | |929| | |937| | |941| |
| |947| | |953| | |967| | |971| | |977| | |983| | |991| | |997| | | |
However, since integers extend to infinity, it is impossible to make a complete list of all prime numbers.
For some mathematicians and researchers, this concept presents a challenge in and of itself. Even if it is theoretically impossible to make a list of all the prime numbers, it is still possible to try to determine the largest of them all.
In 2016, a team of researchers from the University of Central Missouri set up a computer system that allowed them to find a prime number containing 22 338 618 digits, rendering it nearly impossible to read!
A composite number is a number that has three or more positive divisors.
In other words, a composite number can be expressed as the product of two or more (identical or distinct) prime numbers. Therefore, composite numbers can be broken down into their prime factors.
Breaking down a number into its prime factors is called prime factorization.
The number 0
Even if the number |0| has an infinite number of divisors, it is not considered a composite number because it has no prime factorization.
The number 1
The number |1| is not considered a composite number because it does not have at least three divisors.
These two numbers are the only integers that are neither prime nor composite numbers.
All positive integers with a value greater than |1| that are not prime numbers are therefore composite numbers.
Example 1
The positive divisors of |9| are: |1,| |3| and |9.| Since the number |9| has 3 divisors, |9| is a composite number. Being composite, this number can be expressed as a product of prime numbers (prime factors).||9=3\times 3||
Example 2
The positive divisors of |24| are: |1,| |2,| |3,| |4,| |6,| |8,| |12| and |24.| Since the number |24| has more than 3 divisors, |24| is a composite number. Being composite, this number can be expressed as a product of prime numbers (prime factors).||24=2\times2\times2\times3||
Example 3
The positive divisors of |13| are only: |1| and |13.| Since the number |13| does not have 3 or more factors, it is not a composite number. Instead, |13| is a prime number.
A perfect number is a whole number whose sum of its positive divisors (excluding itself) is equal to the number itself.
Example 1
|6| is a perfect number because the sum of its divisors, excluding |6,| is equal to itself.||1+2+3 = 6||
Example 2
|28| is a perfect number because the sum of its divisors, excluding |28,| is equal to itself.||1+2+4+7+14 = 28||
Example 3
|10| is not a perfect number because the sum of its divisors, excluding |10,| is not equal to itself.||1+2+5 \color{#ec0000}{\neq}10||
A square number is a number that can be expressed as |n^2,| where |n| is a natural number.
In other words, it is a number obtained from multiplying a natural number by itself.
Geometrically speaking, square numbers can be represented by points arranged as a square.
Here is a list of the first four square numbers.
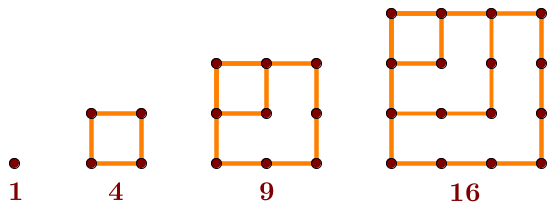
Notice that these numbers can be expressed in the form |n^2.| ||\begin{align}1&=1^2\\4&=2^2\\9&=3^2\\16&=4^2\end{align}||
A triangular number is a number that can be represented by points arranged in the shape of a regular triangle.
Here is a list of the first four triangular numbers.

Square and triangular numbers are called polygonal numbers. They are numbers that can be represented by points arranged in the shape of regular geometric shapes.