Dans le mouvement rectiligne uniforme (MRU) et le mouvement rectiligne uniformément accéléré (MRUA), les mouvements étudiés étaient principalement situés sur l'axe horizontal. Dans la chute libre, le mouvement est positionné sur l'axe vertical. Qu'en est-il d'un mouvement situé entre l'axe horizontal et l'axe vertical? Ces mouvements se font sur une surface appelée plan incliné.
Un plan incliné est une surface plane formant un angle par rapport à l'horizontale.
Si un skieur descend une pente de ski en ligne droite sans zigzaguer, il arrivera au bas de la pente avec une vitesse beaucoup plus élevée que celle qu'il avait en haut de la pente. C'est le même principe pour les rampes qu'utilisent les personnes en fauteuil roulant: une personne qui descend ces rampes arrive en bas de ces dernières avec une vitesse plus élevée que celle du départ (si elle ne freine pas).
Ceci nous démontre qu'il y a un changement de vitesse. Nous ne sommes donc pas en présence d'un MRU, mais bien d'un MRUA. Les équations du MRUA s'appliquent donc lorsqu'un objet est sur un plan incliné. Toutefois, il faut déterminer l'accélération dans cette situation puisque celle-ci dépend de l'inclinaison de la pente.
Supposons qu'une personne se tienne sur le haut d'une pente et qu'on cherche l'accélération que cette personne aurait si elle descendait la pente.
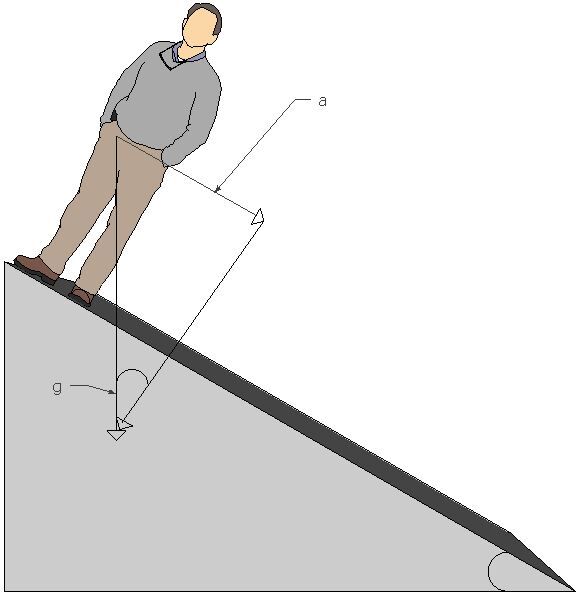
Plus la pente est élevée, plus la personne arrivera rapidement au bas de la pente et plus sa vitesse sera grande. Ainsi, plus l'angle d'inclinaison augmente, plus elle se rapprochera de l'accélération gravitationnelle que subit un corps en chute libre: si la pente était inclinée à |\small 90^{\circ}|, celle personne aurait une accélération de |9,8 \: \text {m/s}^2|. La tendance inverse est également possible: plus l'angle se rapprochera de l'horizontale, plus l'accélération que la personne subit diminuera puisqu'une plus petite composante d'accélération sera exercée sur la personne.
Ainsi, pour toutes les pentes dont l'inclinaison est inférieure à |\small 90^{\circ}|, il existe une formule permettant de calculer la valeur de l'accélération d'un mobile qui se déplace sur un plan incliné. L'accélération sur un plan incliné correspond à une des composantes de l'accélération gravitationnelle.
L'accélération d'un mobile sur un plan incliné se calcule grâce à la formule suivante.
|a = g \times \sin \theta|
où
|a| représente l'accélération du mobile |\small (\text {m/s}^2)|
|g| représente l'accélération gravitationnelle|\small (9,8 \: \text {m/s}^2)|
|\theta| représente l'angle d'inclinaison de la pente |\small (^{\circ})|
Lorsque l'accélération est déterminée, les autres paramètres peuvent être calculés en utilisant les différentes formules de la cinématique.
Un cycliste prend une pause avant de descendre une colline dont l'inclinaison est de |\small 10^{\circ}|. Sachant qu'il a une descente de |\small 120 \: \text {m}| à faire avant d'arriver au pied de la colline, quelle sera la vitesse finale du cycliste s'il ne touche pas aux pédales ni aux freins et qu'il n'y a aucun frottement?
||\begin{align}v_{i} &= 0 \: \text{m/s} &\theta &= 10^{\circ}\\
\triangle x &= 120 \: \text{m} &a &= ? \\ v_{f} &= ?\end{align}||
Trouvons tout d'abord l'accélération du cycliste.
||\begin{align} a = g \times \sin \theta \quad \Rightarrow \quad
a&= 9,8 \: \text{m/s}^{2} \times \sin 10^{\circ}\\
&= 1,70 \: \text{m/s}^2 \end{align}||
Puisque l'accélération a été déterminée, il ne reste qu'à trouver la vitesse finale. En utilisant l'une des équations du MRUA:
||\begin{align} {v_{f}}^2 = {v_{i}}^2 + 2 \cdot a \cdot \triangle x \quad \Rightarrow \quad
{v_{f}}^2 &= (0 \: \text {m/s})^2 + 2 \cdot (1,70 \:\text {m/s}^{2}) \cdot (120 \: \text {m})\\
\sqrt {{v_f}^2} &= \sqrt { 0 + 408 }\\
v_f &= 20,2 \: \text {m/s} \end{align}||
Le cycliste arrivera donc au bas de la colline avec une vitesse de |20,2 \: \text {m/s}|.
Dans le cas d'un mobile se déplaçant sur un plan incliné, des relations graphiques peuvent être déterminées à partir des données obtenues en laboratoire.
Supposons qu'on laisse glisser un mobile sur un plan incliné dont l'inclinaison est de |\small 30^{\circ}| et que la position du mobile en fonction du temps est déterminée.
Position du mobile sur le plan incliné en fonction du temps
| Temps |(\text {s})| | Position |(\text {m})| |
| |0| | |0| |
| |1| | |4,9| |
| |2| | |19,6| |
| |3| | |44,1| |
| |4| | |78,4| |
Graphiquement, la relation obtenue serait une fonction quadratique orientée vers le haut, puisque l'accélération gravitationnelle est orientée dans ce sens. La courbe obtenue est de la même nature que celle tracée dans le cas d'un objet suivant un MRUA.
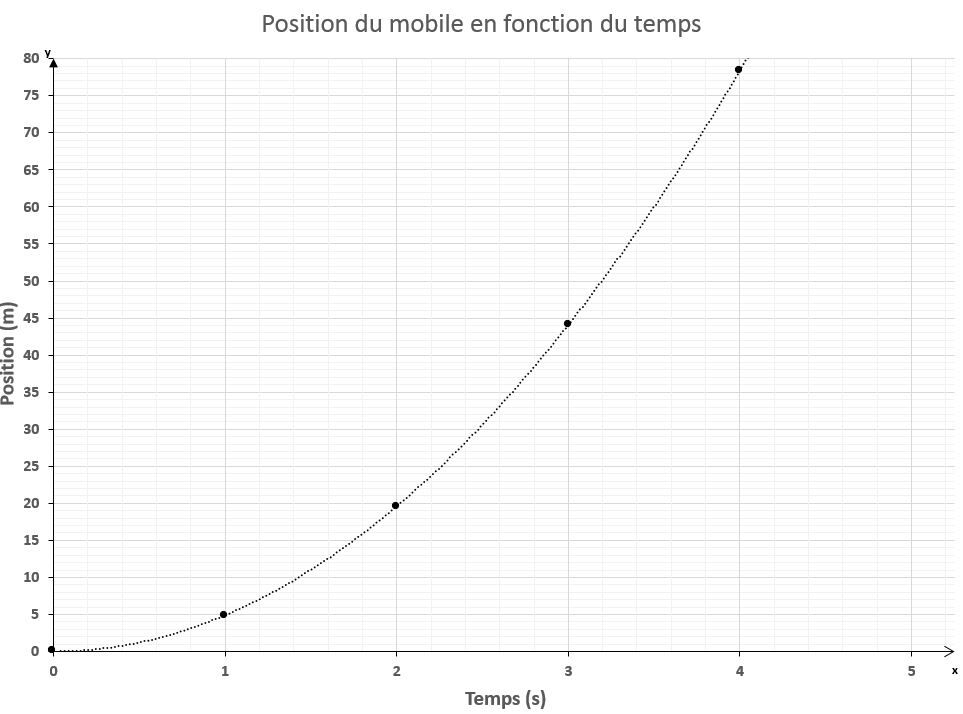
Chaque seconde, le déplacement du mobile est de plus en plus grand en raison de la présence de l'accélération que lui confère l'inclinaison du plan incliné. Le graphique possède les mêmes caractéristiques que le graphique de n'importe quel MRUA.
À partir de ce graphique, il est possible de déterminer la vitesse moyenne en calculant la pente entre deux points. Pour calculer la vitesse instantanée, il faut dessiner la tangente de la courbe au point désiré, puis calculer la pente de cette tangente.
En déterminant la vitesse que le mobile a à différents moments durant sa descente, il est possible de tracer un graphique décrivant la variation de la vitesse en fonction du temps.
| Temps |(\text {s})| | Vitesse |(\text {m/s})| |
| |0| | |0| |
| |1| | |4,9| |
| |2| | |9,8| |
| |3| | |14,9| |
| |4| | |19,6| |
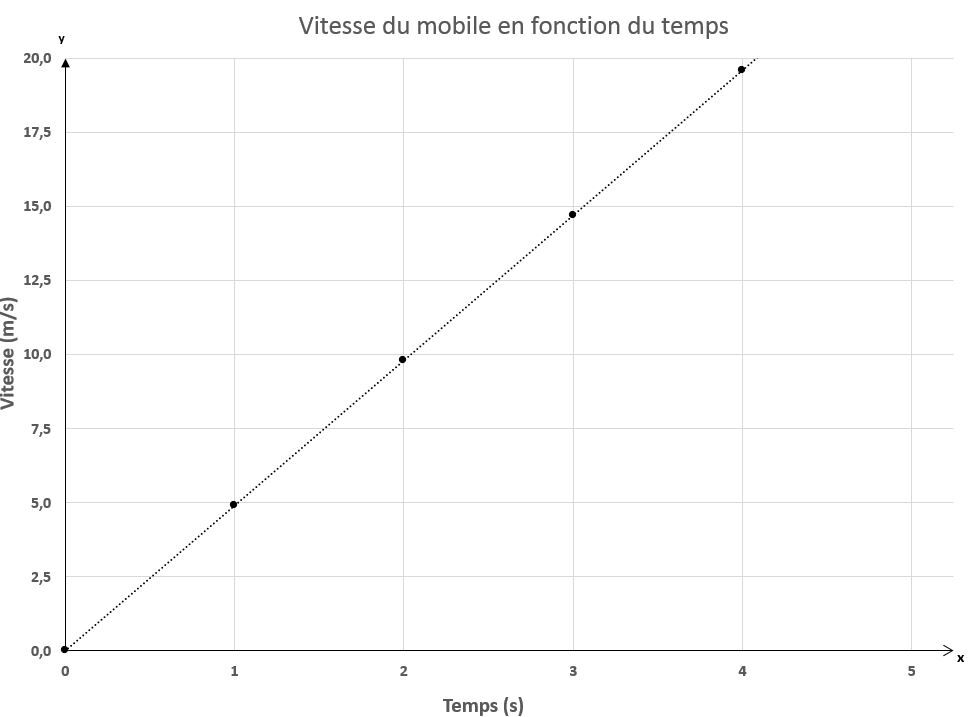
Le graphique obtenu est une relation linéaire croissante. La vitesse augmente de plus en plus au fur et à mesure que le mobile se déplace sur la surface du plan incliné puisqu'une partie de l'accélération gravitationnelle permet au mobile de se déplacer de plus en plus rapidement. L'analyse graphique nous démontre que la vitesse augmente de |\small 4,9 \: \text {m/s}| chaque seconde.
La relation linéaire obtenue est semblable à celle tracée dans un MRUA. Il serait donc possible de calculer l'accélération en déterminant la pente de cette droite. Il serait également possible de savoir la variation de position durant un intervalle de temps en calculant l'aire sous la courbe.
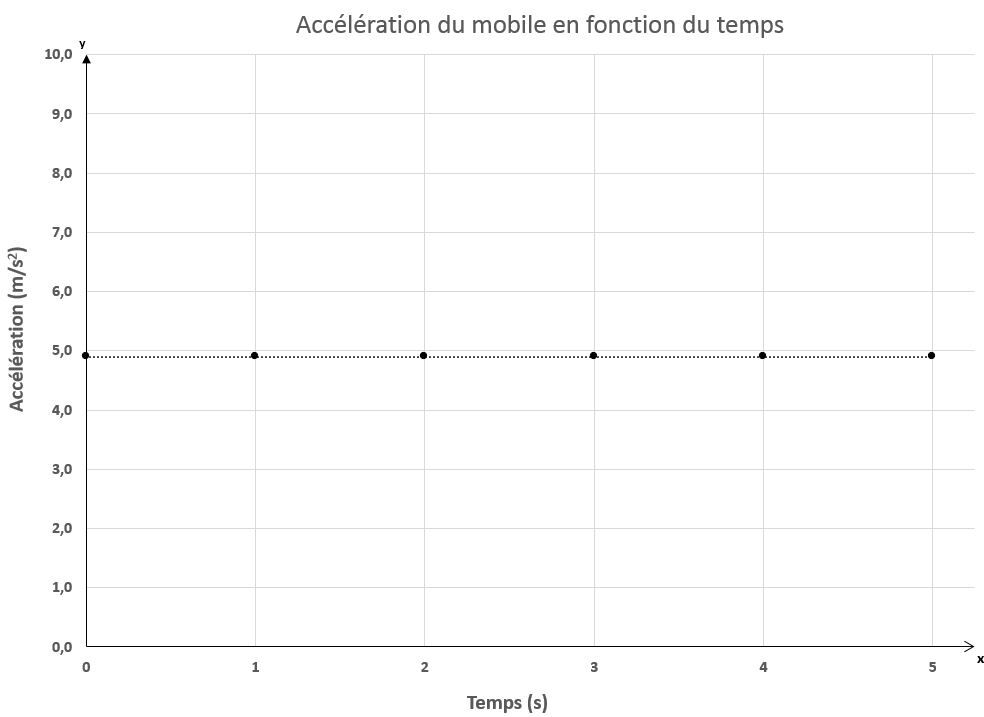
Finalement, le graphique d'accélération en fonction du temps permet d'obtenir une fonction nulle, dont la valeur est toujours égale à la valeur de l'accélération que l'objet a sur le plan. Puisque l'inclinaison du plan était de |\small 30^{\circ}|, l'accélération est donc : |a = 9,8 \times \sin 30^{\circ} = 4,9 \: \text {m/s}^2|.
Accélération du mobile sur le plan incliné en fonction du temps
| Temps |(\text {s})| | Accélération |(\text {m/s}^2)| |
| |0| | |4,9| |
| |1| | |4,9| |
| |2| | |4,9| |
| |3| | |4,9| |
| |4| | |4,9| |