In uniform rectilinear motion (URM) and uniformly accelerated rectilinear motion (UARM), the movements studied were mainly located on the horizontal axis. In free fall, the movement is positioned on the vertical axis. What about a movement located between horizontal and vertical axes? These movements take place on a surface called an inclined plane.
An inclined plane is a flat surface that forms an angle with the horizontal.
If a skier goes down a slope in a straight line without zigzagging, he will arrive at the bottom of the slope with a much higher velocity than he had at the top. The same principle applies to ramps used by wheelchair users: a person descending these ramps arrives at the bottom at a higher velocity than when they started (if they don't brake).
This shows that there is a change in velocity. We are therefore not in the presence of a URM, but a UARM. The UARM equations therefore apply when an object is on an inclined plane. However, we must define the acceleration in this situation, since it depends on the inclination of the slope.
Let's suppose a person is standing on the top of a slope and we're looking for the acceleration that person would have if they went down the slope.
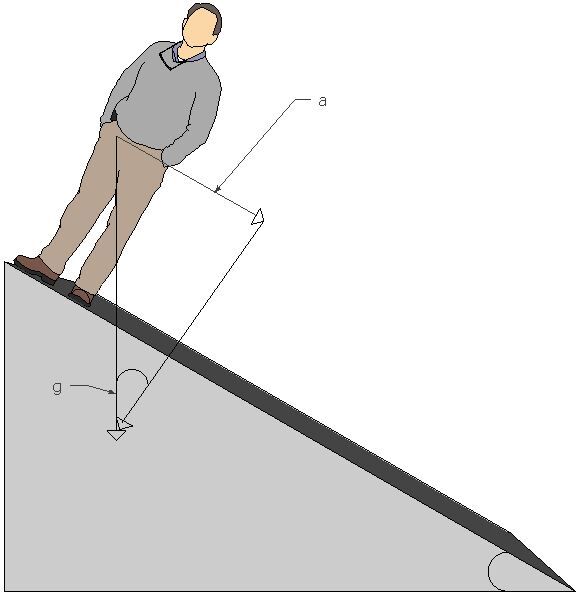
The steeper is the slope, the quicker the person will reach the bottom and the greater will be their velocity. So, as the angle of inclination increases, the acceleration will be closer to the gravitational acceleration experienced by a body in free fall: if the slope were inclined at |\small 90^{\circ}|, the person would have an acceleration of |9.8 \: \text {m/s}^2|. The opposite is also true: as the angle gets closer to the horizontal, the acceleration experienced by the person will decrease as a smaller component of acceleration is applied to the person.
So, for all slopes with an inclination of less than |\small 90^{\circ}|, there is a formula for calculating the acceleration of a moving body on an inclined plane. Acceleration on an inclined plane is one of the components of gravitational acceleration.
The acceleration of a moving body on an inclined plane is calculated using the following formula.
|a = g \times \sin \theta|
where
|a| represents the acceleration of the moving body |\small (\text {m/s}^2)|
|g| represents the gravitational acceleration|\small (9.8 \: \text {m/s}^2)|
|\theta| represents the inclination angle of the slope |\small (^{\circ})|
Once the acceleration has been calculated, the other parameters can be calculated using the various kinematics formulae.
A cyclist takes a break before going down a hill with a |\small 10^{\circ}| gradient. Knowing that he has a descent of |\small 120 \: \text {m}| before reaching the bottom of the hill, what will the cyclist's final velocity be if he doesn't touch the pedals or brakes and there is no friction?
||\begin{align}v_{i} &= 0 \: \text{m/s} &\theta &= 10^{\circ}\\
\triangle x &= 120 \: \text{m} &a &= ? \\ v_{f} &= ?\end{align}||
First, let's find the cyclist's acceleration.
||\begin{align} a = g \times \sin \theta \quad \Rightarrow \quad
a&= 9.8 \: \text{m/s}^{2} \times \sin 10^{\circ}\\
&= 1.70 \: \text{m/s}^2 \end{align}||
Now that the acceleration has been determined, all that remains is to find the final velocity. Using one of the UARM equations:
||\begin{align} {v_{f}}^2 = {v_{i}}^2 + 2 \cdot a \cdot \triangle x \quad \Rightarrow \quad
{v_{f}}^2 &= (0 \: \text {m/s})^2 + 2 \cdot (1.70 \:\text {m/s}^{2}) \cdot (120 \: \text {m})\\
\sqrt {{v_f}^2} &= \sqrt { 0 + 408 }\\
v_f &= 20.2 \: \text {m/s} \end{align}||
The cyclist will therefore reach the bottom of the hill with a velocity of |20.2 \: \text {m/s}|.
In the case of a body moving on an inclined plane, graphical relationships can be determined from data obtained in laboratory conditions.
Let's suppose that a moving body slides on an inclined plane with an inclination of |\small 30^{\circ}| and that the position of the moving body versus time is determined.
Position of the Moving Body on the Inclined Plane vs. Time
| Time |(\text {s})| | Position |(\text {m})| |
| |0| | |0| |
| |1| | |4.9| |
| |2| | |19.6| |
| |3| | |44.1| |
| |4| | |78.4| |
On the graph, the relationship obtained would be an upward- oriented quadratic function, since the gravitational acceleration is oriented in that direction. The curve obtained is similar to the one plotted for an object following a UARM.
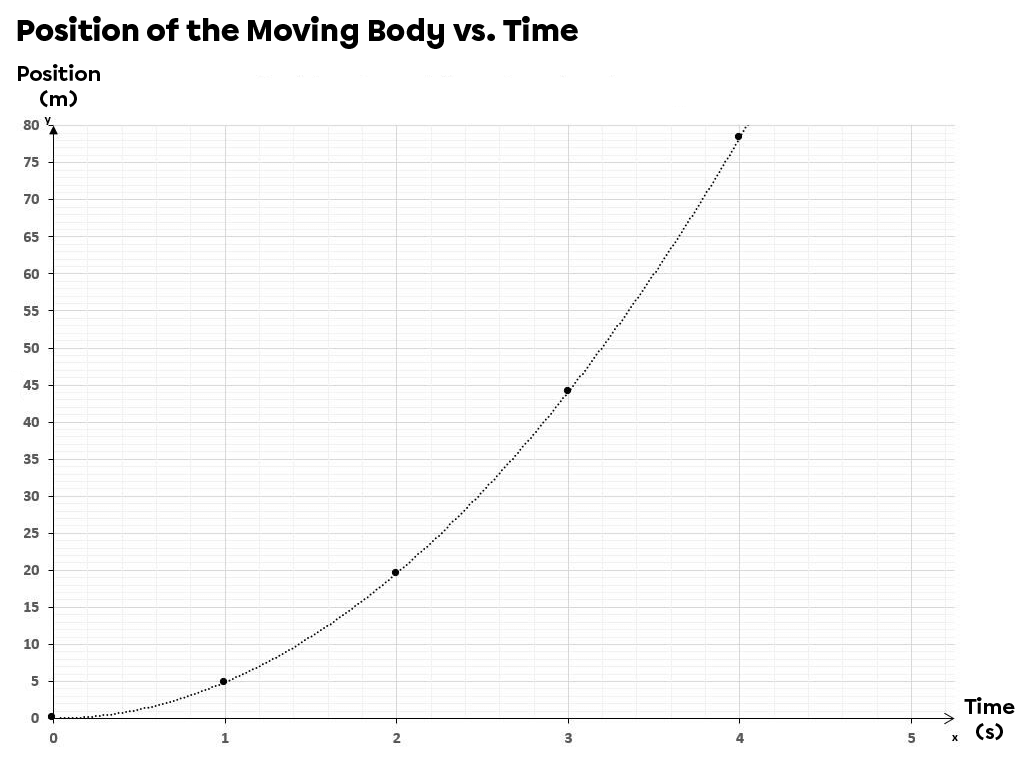
Every second, the moving body's displacement increases as a result of the acceleration provided by the inclined plane. The graph has the same characteristics as the graph for any UARM.
From this graph it is possible to determine the average velocity by calculating the slope between two points. To calculate instantaneous velocity, draw the tangent of the curve at the desired point and then calculate the slope of this tangent.
By finding the velocity of the moving body at different times during its descent, it is possible to draw a graph describing the variation in velocity vs. time.
| Time |(\text {s})| | Velocity |(\text {m/s})| |
| |0| | |0| |
| |1| | |4.9| |
| |2| | |9.8| |
| |3| | |14.9| |
| |4| | |19.6| |
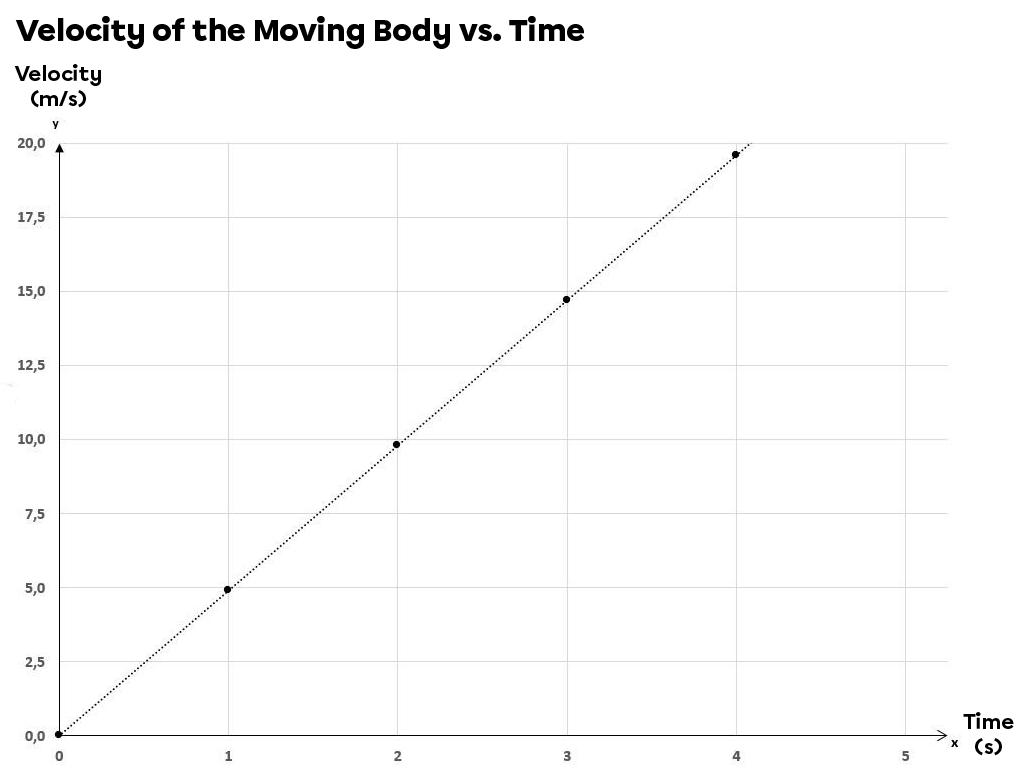
The graph obtained is an increasing linear relationship. The velocity increases more and more as the body moves along the surface of the inclined plane, since part of the gravitational acceleration allows the body to move faster and faster. Graphical analysis shows that the velocity increases by |\small 4.9 \: \text {m/s}| every second.
The linear relationship obtained is similar to the one plotted in a UARM. It would therefore be possible to calculate the acceleration by determining the slope of this straight line. It would also be possible to determine the change in position over a time interval by calculating the area under the curve.
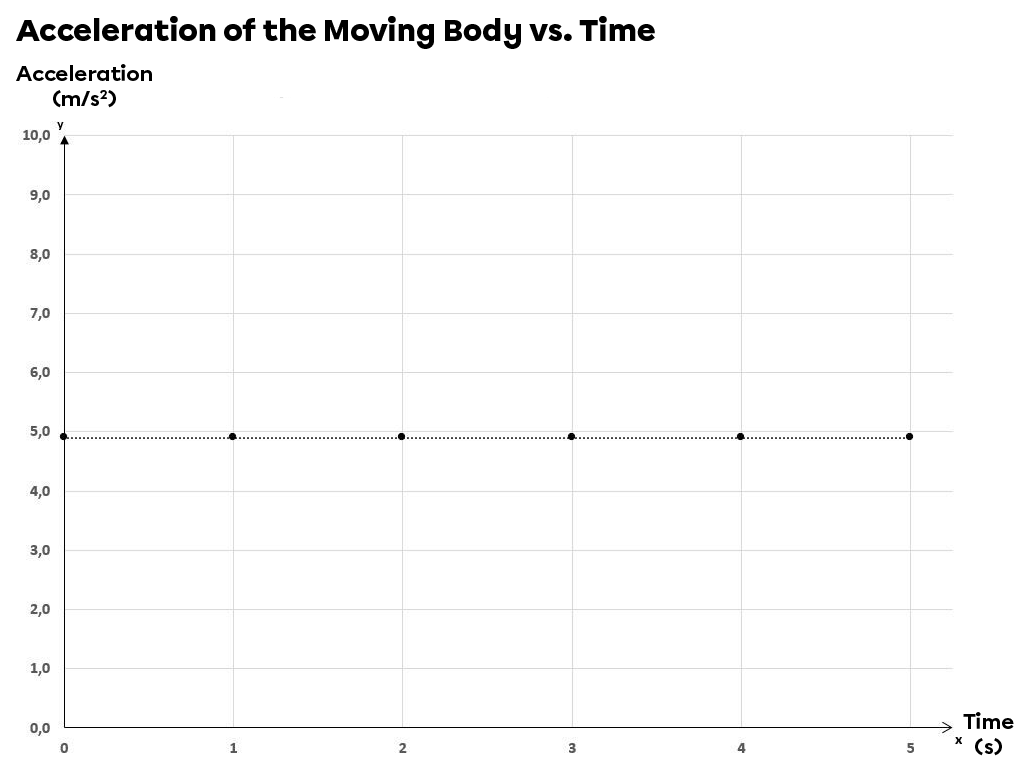
Finally, the acceleration vs. time graph gives a zero function, the value of which is always equal to the value of the acceleration that the object has on the plane. Since the inclination of the plane was |\small 30^{\circ}|, the acceleration is therefore: |a = 9.8 \times \sin 30^{\circ} = 4.9 \: \text {m/s}^2|.
Acceleration of the Moving Body on an Inclined Plane vs. Time
| Time |(\text {s})| | Acceleration |(\text {m/s}^2)| |
| |0| | |4.9| |
| |1| | |4.9| |
| |2| | |4.9| |
| |3| | |4.9| |
| |4| | |4.9| |