Avant d’écouter les vidéos de cette MiniRécup, assure-toi de bien connaitre les formules d’aire et de volume des solides. Il faut aussi que tu sois familier(-ère) avec les méthodes générales de résolution d'équations comme la méthode de la balance. Ces différentes notions te seront essentielles dans ta recherche d’une mesure manquante dans les solides.
La première vidéo ci-dessous s’adresse aux élèves de 2e et de 3e secondaire, car on y explique comment trouver une mesure manquante à partir de l’aire des solides. La deuxième s'adresse aux élèves de 3e secondaire, car on y explique comment trouver une mesure manquante à partir du volume des solides.
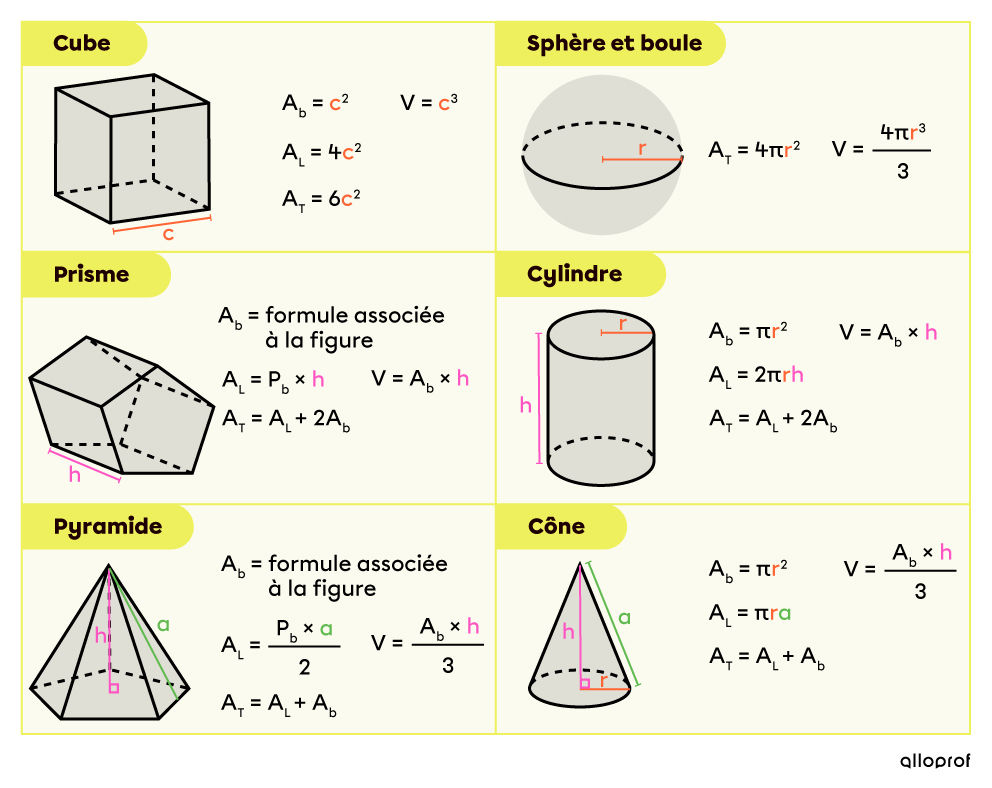
Le tableau suivant est un rappel des différentes formules d’aire et de volume des solides :
Pour trouver une mesure manquante dans un solide, tu dois appliquer l’une des méthodes générales de résolution d'équations sur la formule utilisée dans le problème. Il peut s’agir d’une formule d’aire ou de volume.
Voici un exemple présentant les étapes de résolution à suivre lorsque tu rencontres un problème impliquant la recherche d’une mesure manquante dans les solides :
L’aire latérale d’un prisme régulier à base triangulaire est de 4 284 mm2. Si le côté de sa base mesure 8,5 cm, quelle est la mesure de la hauteur du prisme?
|
Côté de la base : |8{,}5\ \text{cm}=85\ \text{mm}| |
|
|A_L =P_b\times \color{#3A9A38}{h}| |
|
|4\ 284 =(3\times 85)\times \color{#3A9A38}{h}| |
|
|\begin{align}\dfrac{4\ 284}{\color{#EC0000}{255}} &= \dfrac{255\times \color{#3A9A38}{h}}{\color{#EC0000}{255}} \\ 16{,}8\ \text{mm} &= \color{#3A9A38}{h} \end{align}| |
|
Réponse : La hauteur du prisme mesure |16{,}8\ \text{mm}.| |
|