Sometimes, we are given a solid’s volume and all but one of its measurements. So, it is necessary to know how to find a missing measurement.
The procedure for finding a missing measurement in a solid is generally the same regardless of the type of solid. Here are the main steps.
-
Identify the measurements given.
-
Determine the formula to use.
-
Replace the variables with the given measurements.
-
Isolate the sought variable.
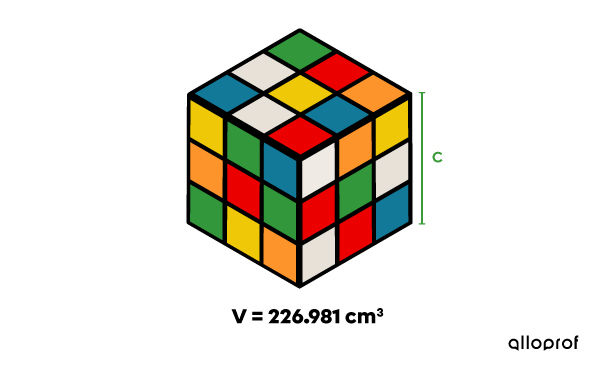
You keep a Rubik's Cube in your backpack to pass the time during breaks at school. With all the school books and supplies you have in your bag, there is only 226.981 cm3 left for the Rubik's Cube.
What should be the maximum measurement of the Rubik's Cube’s edge for it to fit into your backpack?
-
Identify the given measurements
The only measurement provided is the volume of the cube. ||V=226{.}981\ \text{cm}^3|| -
Determine the formula to use
Since the question refers to the volume of a cube, use the following formula: ||V=\color{#3a9a38}{s}^3|| -
Replace the variables with the given measurements
||226{.}981 = \color{#3a9a38}{s}^3|| -
Isolate the sought variable
||\begin{align} \color{#ec0000}{\sqrt[3]{\color{black}{226{.}891}}} &= \color{#ec0000}{\sqrt[3]{\color{#3a9a38}{c}^{\color{black}{3}}}} \\ 6{.}1 \ \text{cm} &\approx \color{#3a9a38}{s}\end{align}||
Answer: The edge of the cube must have a maximum measurement of |6{.}1\ \text{cm}.|
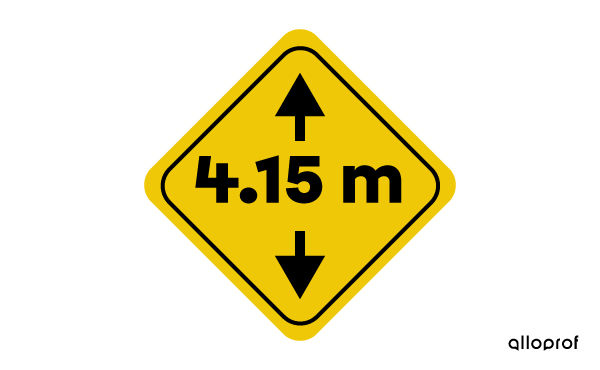
Bobby, a trucker, checks his routes beforehand for the height of the overpasses to avoid damaging his truck and the goods he is transporting. While driving with a big load, he sees the sign below.
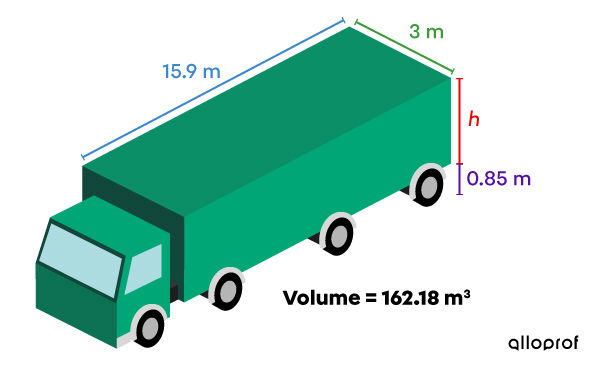
Bobby only knows the volume of the trailer behind his truck, so he stops on the side of the road to check that his truck is not too high to drive under the next overpass.
Since it is impossible for him to reach the top of his truck, what calculations can he use to determine the height of his trailer?
-
Identify the given measurements
Base length: |\color{#3b87cd}{L = 15{.}9\ \text{m}}|
Base Width: |\color{#3a9a38}{l= 3\ \text{m}}|
Wheel height: |\color{#560fa5}{h_\text{wheels}= 0{.}85\ \text{m}}|
Volume of the trailer: |V=162{.}18\ \text{m}^3| -
Determine the formula to use
Since this question refers to volume, use the following formula: ||\begin{align} V &= A_b \times \color{#ec0000}{h} \\ &=(\color{#3a9a38}{l} \times \color{#3b87cd}{L}) \times \color{#ec0000}{h} \end{align}|| -
Replace the variables with the given measurements
||162{.}18 =(\color{#3a9a38}{3} \times \color{#3b87cd}{15{.}9}) \times \color{#ec0000}{h}|| -
Isolate the sought variable
||\begin{align} \color{#ec0000}{\dfrac{\color{black}{162{.}18}}{47{.}7}} &= \color{#ec0000}{\dfrac{\color{black}{47{.}7 \times h}}{47{.}7}} \\ 3{.}4\ \text{m} &= h \end{align}||
Answer: Adding the height of the trailer to the height from the ground gives us |\color{#ec0000}{3{.}4} + \color{#560fa5}{0{.}85} = 4{.}25 \ \text{m}.| Therefore, Bobby’s truck is too high to pass under the bridge |(4{.}25\ \text{m > }4{.}15\ \text{m}).|
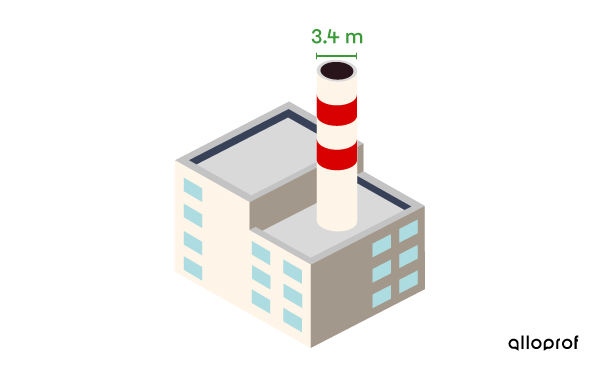
To ensure the effectiveness of air filters, production plants must ensure that their stacks do not contain more than 385 m3 of waste gas.
Based on the building plans, what should the minimum height of the cylindrical chimney be?
-
Identify the given measurements
Chimney diameter: |\color{#3a9a38}{d=3{.}4\ \text{m}}|
Chimney volume: |V=385\ \text{m}^3| -
Determine the formula to use
Since the question refers to the volume of a cylinder, use the following formula: ||\begin{align} V &= A_b \times h\\ &= \pi r^2 \times h \end{align}|| -
Replace the variables with the given measurements
||385 = \pi\left(\dfrac{\color{#3a9a38}{3{.}4}}{2}\right)^2 \times h|| -
Isolate the sought variable
||\begin{align} \color{#ec0000}{\dfrac{\color{black}{385}}{2{.}89\pi}} &= \color{#ec0000}{\dfrac{\color{black}{2{.}89 \pi \times h}}{2{.}89\pi}}\\ 42{.}40 \ \text{m} &\approx h\end{align}||
Answer: The chimney should have a minimum height of approximately |42{.}40\ \text{m}.|
Before playing a game of Bubble soccer, you have to put on some special equipment. In fact, players must wear a huge spherical protective bubble so that they can safely collide with other players.
The only downside is that participants must be at least as tall as the height of the protective bubble. If the volume of a protective bubble is 1.44 m3, what should be the minimum height of the participants?

-
Identify the given measurements
Volume of a ball: |V=1{.}44\ \text{m}^3| -
Determine the formula to use
Since the question concerns the volume of a ball, use the following formula: ||V = \dfrac{4 \pi r^3}{3}||This formula enables us to find the measurement of the radius, which is useful for calculating the total height of a ball. -
Replace the variables with the given measurements
||1{.}44 = \dfrac{4 \pi r^3}{3}|| -
Isolate the sought variable
||\begin{align} 1{.}44 \color{#ec0000}{\times 3} &= \dfrac{4 \pi r^3}{3} \color{#ec0000}{\times 3} \\ \color{#ec0000}{\dfrac{\color{black}{4{.}32}}{4\pi}} &= \color{#ec0000}{\dfrac{\color{black}{4 \pi r^3}}{4\pi}} \\ \color{#ec0000}{\sqrt[3]{\color{black}{0{.}34}}} &\approx \color{#ec0000}{\sqrt[3]{\color{black}{r^3}}}\\ 0{.}70 \ \text{m} &\approx r\end{align}||
Since the height of a ball is twice the radius, we can determine: |\color{#3a9a38}{h} = 0{.}70\times 2 = 1{.}40\ \text{m}.|
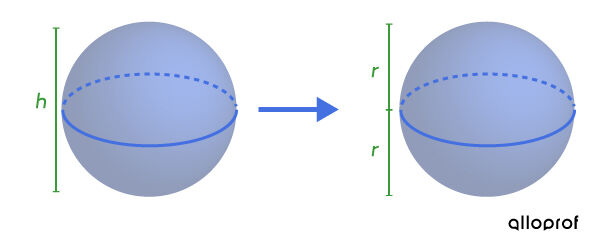
Answer: Participants must be at least |1{.}40\ \text{m}.|
It took 2 592 341 m3 of stone to build the Pyramid of Cheops in Egypt, which is a regular square-based pyramid whose base sides measure 230 m each. What is the pyramid’s height?
-
Identify the given measurements
Base side: |\color{#3a9a38}{s=230\ \text{m}}|
Volume: |V =2\ 592\ 341\ \text{m}^3| -
Determine the formula to use
The formula used to calculate the volume of a pyramid is: ||\begin{align} V &= \dfrac{A_b \times h}{3}\\\\ &= \dfrac{\color{#3a9a38}{s}^2 \times h}{3}\end{align}|| -
Replace the variables with the given measurements
||2\ 592\ 341 = \dfrac{\color{#3a9a38}{230}^2 \times h}{3}|| -
Isolate the sought variable ||\begin{align} 2\ 592\ 341\color{#ec0000}{\times 3} &= \dfrac{\color{#3a9a38}{230}^2 \times h}{3} \color{#ec0000}{\times 3} \\ \color{#ec0000}{\dfrac{\color{black}{7\ 777\ 023}}{52\ 900}} &= \color{#ec0000}{\dfrac{\color{black}{52\ 900 \times h}}{52\ 900}} \\ 147\ \text{m} &\approx h \end{align}||
Answer: The height of the Pyramid of Cheops is approximately |147\ \text{m}.|
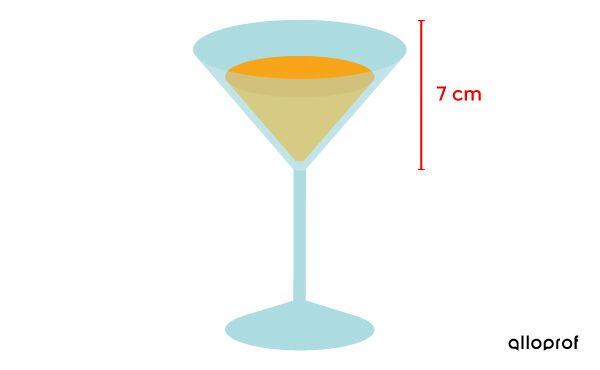
A restaurant owner wants to determine the exact diameter of the drinking glasses in order to ensure a good profit margin.
One drink is usually equivalent to 90 mL, or 90 cm3. To respect this quantity, what diameter should the glass be, considering that the thickness of the glass is negligible?
-
Identify the given measurements
Cone height: |\color{#ec0000}{h=7\ \text{cm}}|
Glass volume: |V_\text{cone}=90\ \text{cm}^3| -
Determine the formula to use
The formula to calculate the volume of a cone is: ||\begin{align} V &= \dfrac{A_b \times \color{#ec0000}{h}}{3}\\\\ &= \dfrac{\pi r^2 \times \color{#ec0000}{h}}{3} \end{align}|| -
Replace the variables with the given measurements ||90 = \dfrac{\pi r^2 \times \color{#ec0000}{7}}{3}||
-
Isolate the sought variable ||\begin{align} 90 \color{#ec0000}{\times 3} &= \dfrac{\pi r^2 \times 7}{3} \color{#ec0000}{\times 3} \\ \color{#ec0000}{\dfrac{\color{black}{270}}{7\pi}} &= \color{#ec0000}{\dfrac{\color{black}{7\pi r^2}}{7\pi}} \\ \color{#ec0000}{\sqrt{\color{black}{12{.}28}}} &\approx \color{#ec0000}{\sqrt{\color{black}{r^2}}}\\ 3{.}5 \ \text{cm} &\approx r \end{align}||
Since we are looking for the measure of the diameter, we must multiply the measure of the radius by |2.| ||\begin{align} d &= 2 \times r \\ &= 2 \times 3{.}5\\ &= 7\ \text{cm} \end{align}||
Answer: The glass’ diameter must be |7\ \text{cm}.| The width and height of the glass are practically identical.
Sometimes, the measure of the apothem of a pyramid or cone must be determined from the volume – even though it is not found in the volume formula. In such cases, find the solid’s height or the base’s radius then calculate the measure of the apothem using the Pythagorean Theorem.
The same process is used to find the measurement of the apothem of a cone or a pyramid. The cone is presented in the following example.
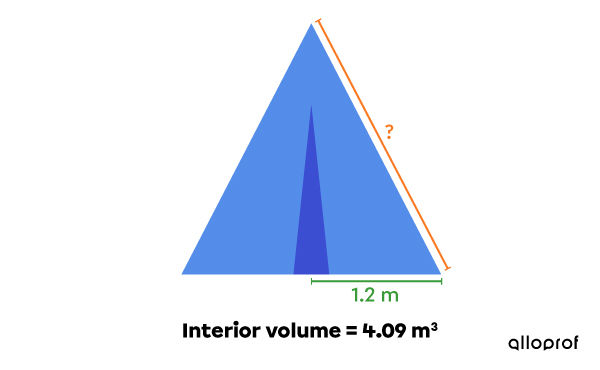
To prevent a cone-shaped tent from blowing away in the wind, anchoring cords connect the tent’s apex to the ground using stakes. These safety cords must run along the tent’s walls.
Using the information provided in the figure below, and knowing that an additional 30 cm must be left at both ends of each anchoring cord for a knot, what is the minimum length of one of the safety cords?
-
Identify the given measurements
Base’s radius: |\color{#3a9a38}{r=1{.}2\ \text{m}}|
Interior volume: |V_\text{cône}=4{.}09\ \text{m}^3| -
Determine the formula to use
We know the volume of the cone, so we use the volume formula even if the apothem does not appear in the formula.||\begin{align} V &= \dfrac{A_b \times h}{3}\\ &=\dfrac{\pi \color{#3a9a38}{r}^2 \times h}{3} \end{align}|| -
Replace the variables with the given measurements
||4{.}09=\dfrac{\pi \color{#3a9a38}{(1{.}2)}^2 \times h}{3}|| -
Isolate the sought variable
||\begin{align} 4{.}09 \color{#ec0000}{\times 3} &= \dfrac{\pi \color{#3a9a38}{(1{.}2)}^2 \times h}{3} \color{#ec0000}{\times 3} \\ \color{#ec0000}{\dfrac{\color{black}{12{.}27}}{1{.}44\pi}} &= \color{#ec0000}{\dfrac{\color{black}{1{.}44\pi \times h}}{1{.}44\pi}} \\ 2{.}71\ \text{m} &\approx h \end{align}||
We are looking for the measure of the apothem – not the height. So, we use the Pythagorean Theorem.
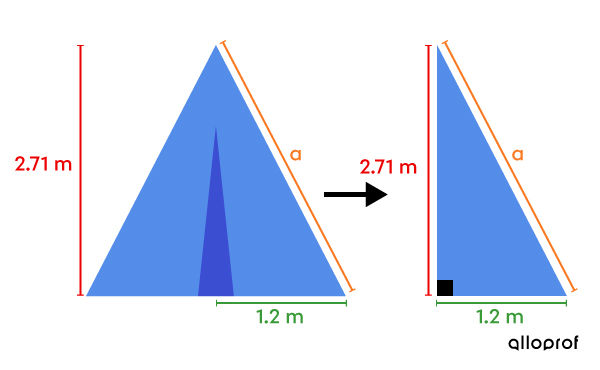
||\begin{align} \color{#ec0000}{a}^2 + \color{#3a9a38}{b}^2 &= \color{#fa7921}{c}^2 \\\\ \color{#ec0000}{2{.}71}^2 + \color{#3a9a38}{1{.}2}^2 &= \color{#fa7921}{a}^2 \\ \color{#ec0000}{\sqrt{\color{black}{8{.}78}}} &\approx \color{#ec0000}{\sqrt{\color{black}{\color{#fa7921}{a}^2}}} \\ 2{.}96 \ \text{m} &\approx \color{#fa7921}{a} \end{align}|| Since we must add |30\ \text{cm}| at each end to make the knots, we get: ||\begin{align} \text{Length of a tie-down}\ &= 2{.}96 + 0{.}3 + 0{.}3 \\ &= 3{.}56 \ \text{m} \end{align}||
Answer: Each anchoring safety cord must have a minimum length of |3{.}56\ \text{m}.|
The previous example shows that we must find the measure of the height before using the Pythagorean Theorem to determine the measure of the apothem. Using the volume to find the measure of a cone or pyramid's apothem requires a few more calculations than simply finding the height.
If we know the lateral area of a cone or a pyramid and the dimensions of the base instead of its volume, the measure of the apothem can be found directly. We can find this measurement in the formula for the lateral area of cones and pyramids: |A_L = \dfrac{P_b \times a}{2}.|
If the height of one of these solids must be found using the lateral area, begin by finding the measure of the apothem. Next, use the Pythagorean Theorem to find the height. Read the concept sheet about finding the measurement of the height of a pyramid or a cone for more information.
Pour valider ta compréhension à propos des mesures manquantes dans les solides de façon interactive, consulte la MiniRécup suivante.

