To successfully calculate a missing measure in a decomposable or truncated solid from the volume, we must create an equation and solve it. To do so, the formulas that enable us to calculate the volume of solids are used. The following is an overview of the process.
-
Determine the volume with which we must work.
-
Identify the missing measurement by using a variable.
-
Associate the volume of each solid with a numerical value or an algebraic expression.
-
Create an equation based on the context.
-
Solve the equation.
-
Interpret the answer according to the context.
When closed, a lunch box looks like the following.
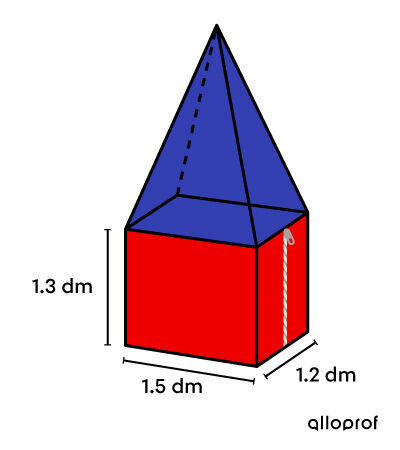
On average, the space available inside a lunch box is |3.65\ \text{dm}^3.| What should be the total height of the lunchbox to respect the standard?
-
Determine the volume
The total volume is |3.65\ \text{dm}^3,| as indicated. -
Identify the missing measure with a variable
The height of the pyramid is not given. It must be taken into account when calculating the volume, thus, we associate the variable |x| to it.

-
Associate the volume of each solid with a numerical value or an algebraic expression
||\begin{align} \color{#333fb1}{V_\text{pyramid}} &=\dfrac{A_b\times h}{3}\\&= \frac{1.5 \times 1.2 \times x}{3} \\ &= \color{#333fb1}{0.6x\ \text{dm}^3} \\\\ \color{#ec0000}{V_\text{prism}} &=A_b\times h\\&= 1.5 \times 1.2 \times 1.3 \\ &= \color{#ec0000}{2.34\ \text{dm}^3} \end{align}|| -
Create an equation based on the context
The volume indicated applies to the whole lunch box. Therefore, the volume of the pyramid and the volume of the prism must be added together.||\begin{align} \text{Total Volume} &= \text{Sum of the volumes of all of the solids} \\ 3.65 &= \color{#333fb1}{0.6x} + \color{#ec0000}{2.34} \end{align}|| -
Solve the equation
||\begin{align} 3.65 \color{#ec0000}{-2.34} &= {0.6x} +{2.34} \color{#ec0000}{-2.34} \\ \color{#ec0000}{\dfrac {\color{black}{1.31}}{0.6}}&= \color{#ec0000}{\dfrac {\color{black}{0.6x}}{0.6}} \\ 2.18 &\approx x \end{align}|| -
Interpret the answer according to the context
||\begin{align}\text{Total height} &= 1.3 + x\\ &= 1.3 + 2.18\\ &=3.48\ \text{dm}\end{align}||
To find a missing measure from the volume of complex solids with 2nd degree equations, the approach is relatively similar to the one involving 1st degree equations. However, the methods for solving them may include factoring with the product-sum method or applying the quadratic formula.
To give a nice shape to various robot toys, they must be adequately stuffed. We use a synthetic material that sells for |$2/\text{dm}^3.| to shape it. To make the final selling price of the product affordable to the maximum number of people possible, we want to limit the cost of stuffing to |$5.60\ | per toy robot.

This model’s head is a cube, the body is a prism with a trapezoidal base, the legs are rectangular-based prisms and the arms are cylinders.
Based on the information in the illustration, how thick should the arms be?
-
Determine the volume
||\begin{align} \text{Total Volume} &= $5.60\div $2/ \text{dm}^3 \\ &= 2.80\ \text{dm}^3\\ &= 2\ 800\ \text{cm}^3 \end{align}|| -
Identify the missing measurement with a variable
We are looking for the thickness of the arm corresponding to the diameter (or double the radius) of the circle forming the base of the cylinder. Associating |x| with the radius makes volume calculations simpler.
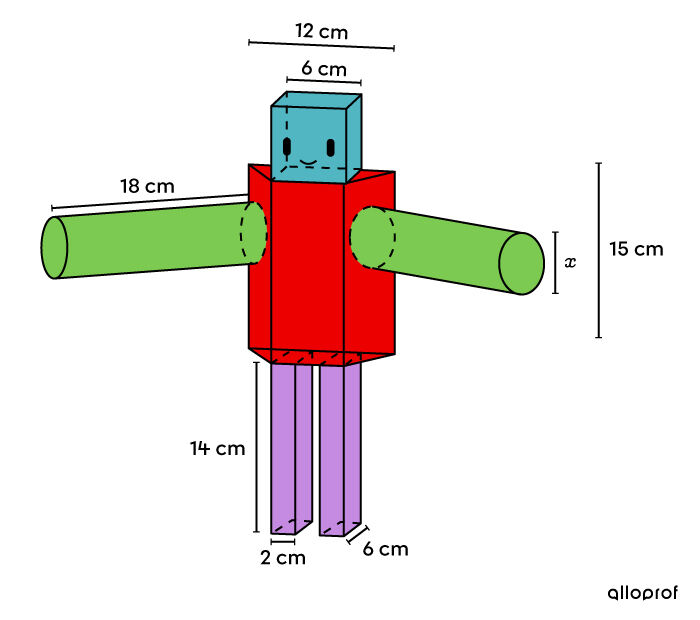
-
Associate the volume of each solid with a numerical value or an algebraic expression
||\begin{align} \color{#333fb1}{V_\text{cube}}&=c^3\\ &= 6^3 \\
&= \color{#333fb1}{216\ \text{cm}^3}\\\\
\color{#ff55c3}{V_\text{prism}}&=A_b \times h\\ &= 6 \times 2 \times 14\\
&= \color{#ff55c3}{168\ \text{cm}^3}\\\\
\color{#ec0000}{V_\text{prism}} &= A_b \times h \\ &= \displaystyle \left(\frac{(6+12)\times 6}{2}\right) \times 15 \\ &= \color{#ec0000}{810\ \text{cm}^3}\\\\
\color{#3a9a38}{V_\text{cylinder}} &=A_b \times h \\ &= \pi x^2 \times 18\\
&= \color{#3a9a38}{18\pi x^2\ \text{cm}^3} \end{align}|| -
Create an equation based on the context
||\begin{align} \text{Total Volume} &= \text{Sum of the Volume of all of the Solids} \\ 2\ 800 &= \color{#333fb1}{216} + 2 \times \color{#ff55c3}{168}+ \color{#ec0000}{810} + 2 \times \color{#3a9a38}{18\pi x^2} \\ 2\ 800 &= \color{#333fb1}{216} + \color{#ff55c3}{336}+ \color{#ec0000}{810} + \color{#3a9a38}{36\pi x^2} \end{align}|| -
Solve the equation
||\begin{align} 2\ 800 &= 1 \ 362 + 36\pi x^2 \\ 2\ 800\color{#ec0000}{-1 \ 362} &= 1 \ 362 \color{#ec0000}{-1 \ 362}+ 36\pi x^2 \\ \color{#ec0000}{\dfrac{\color{black}{1\ 438}}{36\pi } }&= \color{#ec0000}{\dfrac{\color{black}{36\pi x^2}}{36\pi }}\\ \color{#ec0000}{\sqrt{\color{black}{12.71}}} &\approx \color{#ec0000}{\sqrt{\color{black}{x^2}}} \\ 3.57 &\approx x \end{align}|| -
Interpret the answer according to the context
||\begin{align} \text{Thickness of arm} &=2 \times \text{radius}\\ &= 2 \times 3.57\\ &= 7.14\ \text{cm}\end{align}||
A truncated solid is a solid where a portion has been removed. Thus, to find a missing measure in a truncated solid, one must consider the original solid and subtract appropriately.
To improve its brand, a company wants to change the shape of an orange juice carton. However, the company wants the new model to be based on the old one. Thus, the red section was obtained by horizontally truncating the pink pyramid of the old model. Finally, the total height of the carton remains the same, i.e., |21\ \text{cm}.|
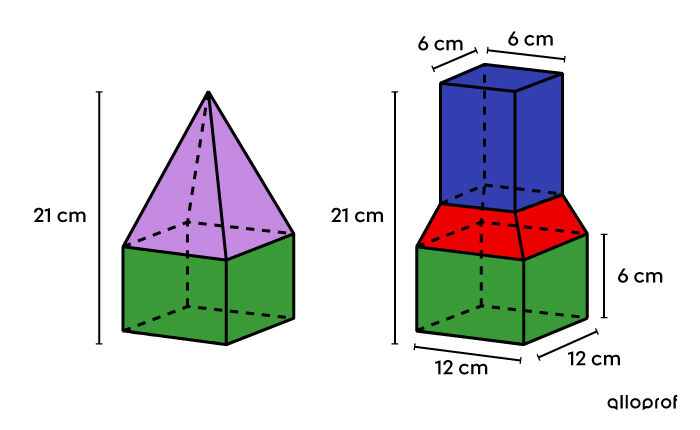
Based on the information provided in the drawing, what should be the height measurement of the new container’s top since the new model’s volume is |1\ 872\ \text{cm}^3?|
-
Determine the volume
According to the problem, the total volume of the new container is |1\ 872\ \text{cm}^3.| -
Identify the missing measure with a variable
We are looking for the height of the blue prism.
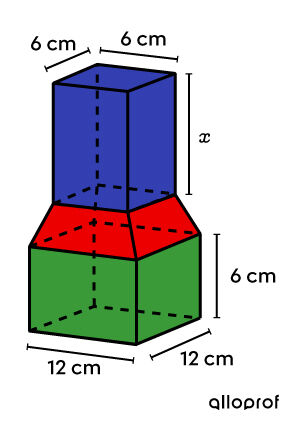
-
Associate the volume of each solid with a numerical value or an algebraic expression
||\begin{align} \color{#333fb1}{V_\text{prism}} &= A_b \times h \\ &= 6^2\times x \\ &= \color{#333fb1}{36 x\ \text{cm}^3}\\\\ \color{#3a9a38}{V_\text{prism}} &= A_b \times h \\ &= 12^2 \times 6 \\ &= \color{#3a9a38}{864\ \text{cm}^3}\\\\ \end{align}||Next, we must determine the volume of the truncated pyramid by taking into account the initial pyramid.The height of the pink pyramid (of the original model) is ||\begin{align} \text{Height of the pink pyramid} &= 21 - 6 \\ &= 15\ \text{cm}\end{align}|| Since the new model has the same height as the original, the height of the section of pyramid that has been removed is identical to the height of the blue prism in the new model.
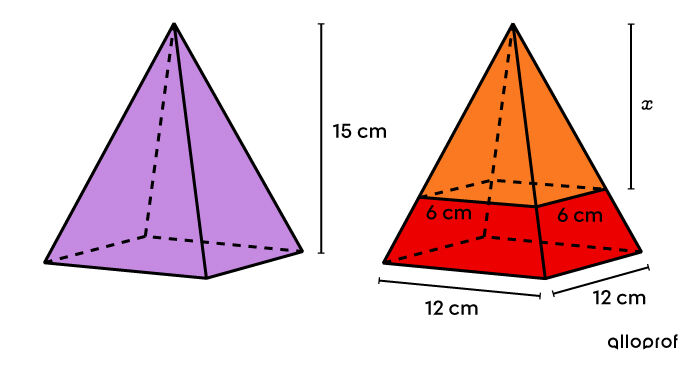
||\begin{align} \color{#ec0000}{V_\text{truncated pyramid}} &= \color{#c58ae1}{V_\text{pyramid}} - \color{#fa7921}{V_\text{pyramid}} \\ &= \color{#c58ae1}{\dfrac{A_b \times h}{3}}- \color{#fa7921}{\dfrac{A_b \times h}{3}}\\ &= \color{#c58ae1}{\dfrac{12^2 \times 15}{3}} -\color{#fa7921}{\frac{6^2\times x}{3}} \\ &= \color{#ec0000}{720 - 12x} \end{align}||
-
Create an equation based on the context
||\begin{align} \text{Total Volume} &= \text{Sum of the volumes of all of the solids} \\ 1\ 872 &= \color{#333fb1}{36x} + \color{#3a9a38}{864} + \color{#ec0000}{720 - 12x} \\ \end{align}|| -
Solve the equation
||\begin{align} 1\ 872 &= 24x + 1\ 584 \\ 1\ 872 \color{#ec0000}{-1\ 584}&= 24x + 1\ 584 \color{#ec0000}{-1\ 584} \\ \color{#ec0000}{\dfrac {\color{black}{288}}{24}}&= \color{#ec0000}{\dfrac {\color{black}{24x}}{24}}\\ 12 &= x \end{align}|| -
Interpret the answer according to the context
The height of the top of the new container is |12\ \text{cm}.|
A decomposable solid is a solid that can be separated into several simpler solids. To find a missing measure in a decomposable solid, we usually decompose it by identifying individual solids and subtracting the ones that are removed.
With Christmas approaching, a new product is arriving on the market. It is a cubic-shaped snow globe made of glass. Inside is a cylindrical cavity where you insert a photo of a loved one.
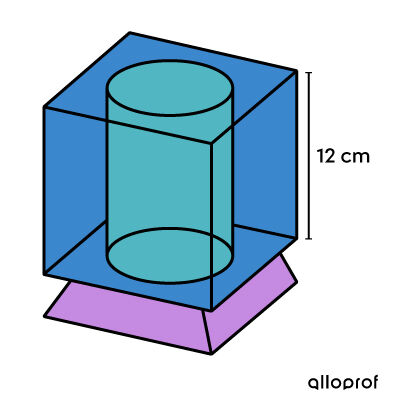
To ensure the movement of the artificial snowflakes in the enclosed section of the cube, it is filled |90\ \%| with a liquid, representing |1.010 \, 7\ \text{L}| of liquid. Based on the information, determine the diameter of the product’s cylindrical cavity.
-
Determine the volume
We can create a proportion using the information in the problem. ||\begin{align} \frac{90}{100} &= \frac{1.010 \, 7\ \text{L}} {?\ \text{L}}\\\\ ?&=\dfrac{100\times 1.010 \, 7}{90}\\?&=1.123\ \text{L}\\ ?&=1.123\ \text{dm}^3\\?&=1\ 123\ \text{cm}^3 \end{align}|| -
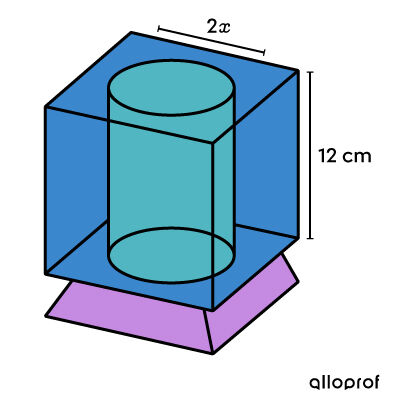
Identify the missing measure with a variable
We are looking for the diameter of the cylinder. Since we need the radius in the calculations, we choose |2x| to represent the diameter. Thus, |x| is the radius.
-
Associate the volume of each solid with a numerical value or an algebraic expression
||\begin{align}{V_\text{cube}} &= c^3 \\ &= 12^3 \\ &={1\ 728\ \text{cm}^3} \\\\ V_\text{cylinder} &= A_b \times h \\&= \pi x^2 \times 12\\ &= 12\pi x^2\ \text{cm}^3 \end{align}|| -
Create an equation based on the context
||\begin{align} \color{#333fb1}{V_\text{total}} &= V_\text{cube} - V_\text{cylinder} \\ \color{#333fb1}{1\ 123} &= 1\ 728 - 12\pi x^2 \end{align}|| -
Solve the equation
||\begin{align} \color{#333fb1}{1\ 123} \color{#ec0000}{-1\ 728} &= 1\ 728\color{#ec0000}{-1\ 728} - 12\pi x^2 \\
\color{#ec0000}{\dfrac{\color{black}{-605}}{-12\pi }} &= \color{#ec0000}{\dfrac{\color{black}{-12\pi x^2}}{-12\pi }} \\
\color{#ec0000}{\sqrt{\color{black}{16.05}}} &\approx \color{#ec0000}{\sqrt{\color{black}{x^2}}} \\ 4.01 &\approx x \end{align}||Thus, the radius of the cylinder is about |4.01\ \text{cm}.| -
Interpret the answer according to the context
||\begin{align} \text{Diameter} &= 2x\\ &= 2 \times 4.01 \\ &=8.02\ \text{cm} \end{align}||
To confirm you understand how to find missing measurements in solids, see the following interactive CrashLesson:
