In some problems, the solid’s area and all of its measurements, except one, are given. In these cases, it is necessary to know how to find this missing measurement.
The procedure for finding a solid’s missing measurement is generally the same regardless of the type of solid. The following are the main steps.
-
Identify the measurements given.
-
Determine the formula to use.
-
Replace the variables with the given measurements.
-
Isolate the sought variable.
A toy company wants to replace some of the sides of their cardboard boxes with a thick transparent material to enable customers to see the packaged products inside. To order the material, the company needs to know the box’s dimensions. Given that the total area of the box is |2\ 646\ \text{cm}^2,| determine the measure of the box’s edges.

-
Identify the measurements given
Total area of the box: |A_T=2\ 646 \ \text{cm}^2| -
Determine the formula to use
Since the question refers to the surface area, use the following formula: ||A_T = 6 s^2|| -
Replace the variables with the given measurements ||2 \ 646 = 6 \color{#7CCA51}{s}^2||
-
Isolate the sought variable ||\begin{align} 2 \ 646 &= 6 \color{#7CCA51}{c}^2 \\ \color{#EC0000}{\frac{\color{black}{2 \ 646}}{6}} &= \color{#EC0000}{\frac{\color{black}{6}\color{#7CCA51}{s}^\color{black}{2}}{6}} \\ 441 &= \color{#7CCA51}{s}^2\\ \color{#EC0000}{\sqrt{\color{black}{441}}} &= \color{#EC0000}{\sqrt{\color{#7CCA51}{s}^\color{black}{2}}}\\ 21\ \text{cm} &= \color{#7CCA51}{s}\end{align}||
Answer: The measure of the cube’s edge is |21\ \text{cm}.|
Before making a delivery, a trucker must ensure that the dimensions of the object being transported does not exceed the width of the trailer. He only has access to the measurements identified in the following image for his next delivery. Help him determine the measure of the box’s width.
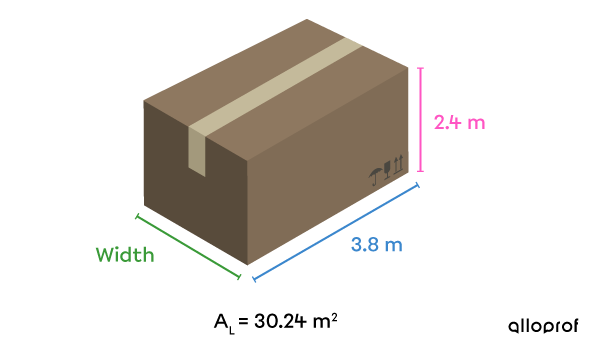
-
Identify the given measurements
Lateral area of the box: |A_L=30{.}24\ \text{m}^2|
Base length: |\color{#3B87CD}{L}=3{.}8\ \text{m}|
Box height: |\color{#FF55C3}{h}=2{.}4\ \text{m}| -
Determine the formula to use
Since the question refers to the lateral area of a rectangular-based prism, use the following formula: ||A_L = P_b \times h|| -
Replace the variables with the given measurements ||30{.}24 = (\color{#3A9A38}{l} +\color{#3A9A38}{l} + \color{#3B87CD}{3{.}8} + \color{#3B87CD}{3{.}8}) \times \color{#FF55C3}{2{.}4}||
-
Isolate the sought variable ||\begin{align} 30{.}24 &=(\color{#3A9A38}{l} +\color{#3A9A38}{l} + \color{#3B87CD}{3{.}8} + \color{#3B87CD}{3{.}8}) \times \color{#FF55C3}{2{.}4}\\ 30{.}24 &= (2\color{#3A9A38}{l} + 7{.}6)\times 2{.}4 \\ 30{.}24 &= 4{.}8 \color{#3A9A38}{l} + 18{.}24\\ 30{.}24 \color{#EC0000}{- 18{.}24} &= 4{.}8 \color{#3A9A38}{l} +18{.}24 \color{#EC0000}{ - 18{.}24}\\ 12 &= 4{.}8 \color{#3A9A38}{l}\\ \color{#EC0000}{\dfrac{\color{black}{12}}{4{.}8}} &= \color{#EC0000}{\dfrac{\color{black}{4{.}8}\color{#3A9A38}{l}}{4{.}8}}\\ 2{.}5\ \text{m} &= \color{#3A9A38}{l}\end{align}||
Answer: The width of the rectangular-based prism is |2{.}5\ \text{m}.|
Sergei wants to coat his new lidded, cylindrical trash can with an anti-rust coating. His neighbour tells him about a product that covered his |1{.}335\ \text{m}^2| garbage can with a single coat. However, Sergei's trash can is twice as tall as his neighbour's. If the diameter of his neighbour’s garbage is |0{.}5\ \text{m}|, how tall is Sergei's trash can?
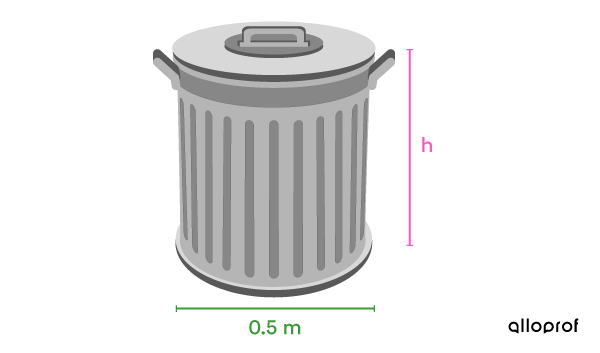
-
Identify the given measurements
Total area of neighbour's trash can: |A_T=1{.}335\ \text{m}^2|
Diameter of the neighbour's trash can: |\color{#3A9A38}{d=0{.}5\ \text{m}}| -
Determine the formula to use
Since the question refers to the surface area of a cylinder, use the following formula: ||A_T = 2A_b+A_L|| -
Replace the variables with the given measurements
In this case, divide the diameter of the bin by 2 to obtain the radius needed in the formula. ||\begin{align}\color{#7CCA51}{\text{radius}}&=\color{#3A9A38}{\text{diameter}}\div2\\&=\color{#3A9A38}{0{.}5}\div2\\&=\color{#7CCA51}{0{.}25\ \text{m}}\end{align}|| ||\begin{align}A_T &= 2\times \pi \color{#7CCA51}r^2+2 \pi \color{#7CCA51}r \color{#FF55C3}{h}\\ 1{.}335 &=2\times \pi(\color{#7CCA51}{0{.}25})^2+ 2\pi (\color{#7CCA51}{0{.}25}) \times \color{#FF55C3}{h}\end{align}|| -
Isolate the sought variable
||\begin{align}1{.}335 &=2\times \pi(\color{#7CCA51}{0{.}25})^2+ 2\pi (\color{#7CCA51}{0{.}25}) \times \color{#FF55C3}{h}\\1{.}335&\approx 0{.}39 + 1{.}57\color{#FF55C3}{h}\\1{.}335\color{#EC0000}{-0{.}39}&\approx 0{.}39 + 1{.}57\color{#FF55C3}{h}\color{#EC0000}{-0{.}39}\\ 0{.}945&\approx1{.}57\color{#FF55C3}{h}\\ \color{#EC0000}{\dfrac{\color{black}{0{.}945}}{1{.}57}}&\approx \color{#EC0000}{\dfrac{\color{black}{1{.}57}\color{#FF55C3}{h}}{1{.}57}}\\0{.}60\ \text{m}&\approx\color{#FF55C3}{h}\end{align}||
Answer: Since Sergei's trash can is twice as high as his neighbour's, the height of Sergei's trash can is approximately |2\times 0{.}6=1{.}2\ \text{m}.|
What is the measure of a tennis ball’s radius if a cylindrical container that can hold exactly 3 balls has a lateral area of |379{.}84\ \text{cm}^2|?
-
Identify the given measurements
Lateral area of the container: |A_L=379{.}84\ \text{cm}^2| -
Determine the formula to use
Since the question refers to the lateral area of a cylinder, use the following formula: ||A_L = 2 \pi rh|| -
Replace the variables with the given measurements
In this case, the height measurement can be found using the ball’s radius.
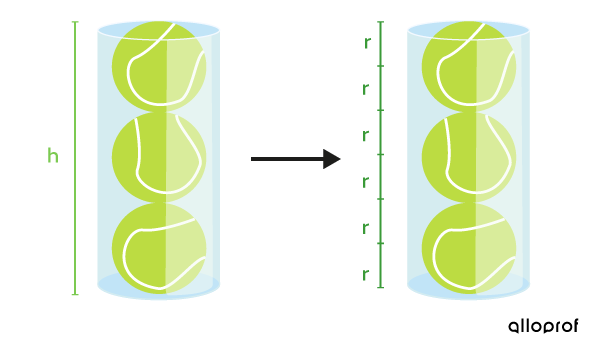
||\begin{align} A_L &= 2 \pi r \times \color{#7CCA51}{h}\\ 379{.}84 &= 2 \pi r \times \color{#7CCA51}{6}\color{#3A9A38}{r}\end{align}||
-
Isolate the sought variable
||\begin{align} 379{.}84 &= 2 \pi \color{#3A9A38}{r} \times 6\color{#3A9A38}{r}\\ \color{#ec0000}{\dfrac{\color{black}{379{.}84}}{12\pi}} &= \color{#ec0000}{\dfrac{\color{black}{12 \pi\color{#3A9A38}{r}^2}}{12\pi}} \\ \color{#ec0000}{\sqrt{\color{black}{10{.}08}}} &\approx \color{#ec0000}{\sqrt{\color{#3A9A38}{r}^{\color{black}{2}}}}\\ 3{.}17\ \text{cm} &\approx \color{#3A9A38}{r}\end{align}||
Answer: The tennis balls have a radius of approximately |3{.}17\ \text{cm}.|
Gabriela wants to buy a decorative incense burner for her living room. The burner is a regular octagonal pyramid. Gabriela doesn't know if it can fit on a shelf |15\ \text{cm}| deep.
Gabriela knows the total area of the incense burner is |789{.}12\ \text{cm}^2.| The apothem of the pyramid is |15\ \text{cm}| and the measure of one side of the octagon is |8\ \text{cm}.|
Can the incense burner fit on the shelf if the base’s apothem |(\color{#3B87CD}{a_b})| is perpendicular to the wall?
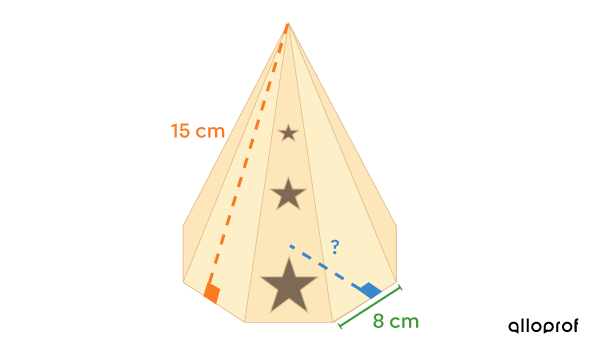
-
Identify the given measurements
Total area of the pyramid: |A_T=789{.}12 \ \text{cm}^2|
Apothem of the pyramid: |\color{#FA7921}{a_p=15\ \text{cm}}|
Measure of the sides of the octagon: |\color{#3A9A38}{s=8\ \text{cm}}|
Number of sides of an octagon: |n=8\ \text{sides}| -
Determine the formula to use
In the case of a regular octagonal pyramid, the formula for calculating the total area is: ||\begin{align}A_T &= A_L+A_B\\&=\dfrac{P_b\times \color{#FA7921}{a_p}}{2}+\dfrac{\color{#3A9A38}{s}\times \color{#3B87CD}{a_b}\times n}{2}\end{align}|| -
Replace the variables with the given measurements
||\begin{align}789{.}12&=\dfrac{(8\times \color{#3A9A38}{8})\times\color{#FA7921}{15}}{2}+\dfrac{\color{#3A9A38}{8}\times \color{#3B87CD}{a_b}\times 8}{2}\end{align}|| -
Isolate the sought variable
||\begin{align}789{.}12&=480+32\color{#3B87CD}{a_b}\\789{.}12\color{#EC0000}{-480}&=480+32\color{#3B87CD}{a_b}\color{#EC0000}{-480}\\309{.}12&=32\color{#3B87CD}{a_b}\\\ \color{#EC0000}{\dfrac{\color{black}{309{.}12}}{32}}&=\color{#EC0000}{\dfrac{\color{black}{32}\color{#3B87CD}{a_b}}{32}}\\9{.}66\ \text{cm}&=\color{#3B87CD}{a_b}\end{align}||
Answer: Since the apothem of the base is |9{.}66\ \text{cm},| the width of the pyramid, if it is perpendicular to the wall, is |2\times 9{.}66=19{.}32\ \text{cm}.| Because the shelf measures |15\ \text{cm},| the incense burner will not fit.
Since a regular pyramid is, in fact, a pyramid with a regular polygon as its base, be careful not to confuse the base’s apothem with that of the pyramid.
The apothem is usually identified by the variable |a.| To differentiate between the two apothems, add a subscript. Thus, the pyramid’s apothem becomes |a_p| and the base’s apothem becomes |a_b.| The choice of the subscript or the way of identifying the 2 measures may vary in different contexts.
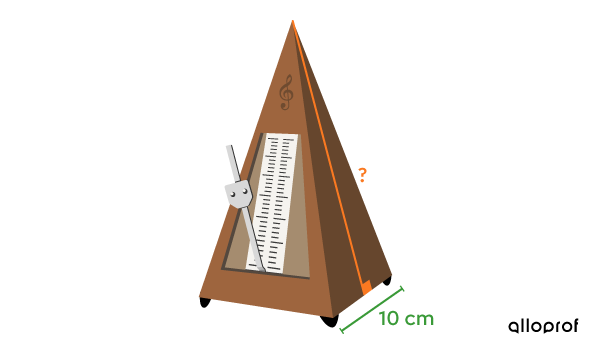
Stefan plays piano and he frequently uses an old metronome that is shaped like a square-based pyramid.
To polish the metronome, he needs to know the measure of the pyramid’s apothem. He knows that the base of the metronome measures |10\ \text{cm}| and the total area of the pyramid is |512{.}4\ \text{cm}^2.|
What is the measure of the metronome’s apothem?
-
Identify the given measurements
Total area of the pyramid: |A_T=512{.}4 \ \text{cm}^2|
Measure of the sides of the square base: |\color{#3A9A38}{s=10\ \text{cm}}| -
Determine the formula to use
In the case of a regular square pyramid, the formula for calculating the total area is: ||\begin{align}A_T &= A_L+A_B\\&=\dfrac{P_b\times \color{#FA7921}{a_p}}{2}+\color{#3A9A38}{s}^2\end{align}|| -
Replace the variables with the given measurements
||\begin{align}512{.}4&=\dfrac{(4\times \color{#3A9A38}{10})\times\color{#FA7921}{a_p}}{2}+\color{#3A9A38}{10}^2\end{align}|| -
Isolate the sought variable
||\begin{align}512{.}4&=20\color{#FA7921}{a_p}+100\\512{.}4\color{#EC0000}{-100}&=20\color{#FA7921}{a_p}+100\color{#EC0000}{-100}\\412{.}4&=20\color{#FA7921}{a_p}\\\ \color{#EC0000}{\dfrac{\color{black}{412{.}4}}{20}}&=\color{#EC0000}{\dfrac{\color{black}{20\color{#FA7921}{a_p}}}{20}}\\20{.}62\ \text{cm}&=\color{#FA7921}{a_p}\end{align}||
Answer: The apothem of the metronome is |20{.}62\ \text{cm}.|
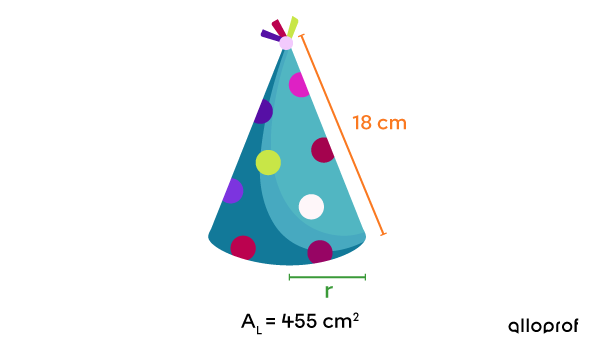
Parents bought cone-shaped party hats to distribute to all the guests at their child’s birthday party. To ensure that the model found online is large enough for the children's heads, they need to know the measure of the circle’s radius at the base of the hat.
-
Identify the given measurements
Lateral area of the cone: |A_L=455\ \text{cm}^2|
Measure of the cone’s apothem: |\color{#FA7921}{a=18\ \text{cm}}| -
Determine the formula to use
The formula for calculating the lateral area of the cone is: ||A_L = \pi \times \color{#3A9A38}{r} \times \color{#FA7921}{a}|| -
Replace the variables with the given measurements ||455 = \pi \times\color{#3A9A38}{r} \times \color{#FA7921}{18}||
-
Isolate the sought variable ||\begin{align} \color{#EC0000}{\dfrac{\color{black}{455}} {18}} &= \color{#EC0000}{\dfrac{\color{black}{\pi \color{#3A9A38}{r} \times \color{#FA7921}{18}}}{18}}\\ 25{.}28 &\approx \pi \color{#3A9A38}{r}\\ \color{#EC0000}{\dfrac{\color{black}{25{.}28}}{\pi}} &\approx \color{#EC0000}{\dfrac{\color{black}{\pi}\color{#3A9A38}{r}}{\pi}} \\ 8{.}05\ \text{cm} &\approx \color{#3A9A38}{r}\end{align}||
Answer: The party hat has a radius of approximately |8{.}05\ \text{cm}.|
Since pyramids and cones have a similar shape, the procedure for finding the measurement of the cone’s apothem is the same as that of a pyramid.
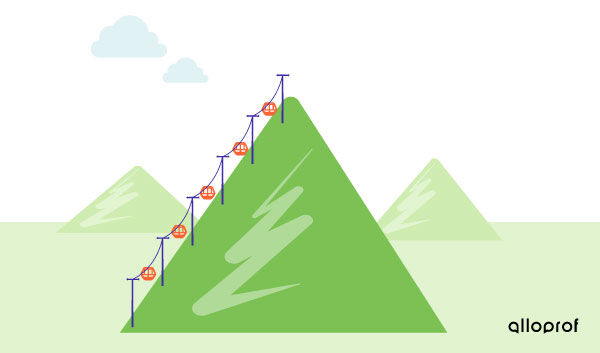
A resort wants to install a ski lift to provide a panoramic view. To complete this project, the resort needs to know the distance between the foot of the mountain and the summit.
Using topographic maps of the region, the lateral area of the conical-shaped mountain is estimated to be |1{.}7\ \text{km}^2| and the measurement of the radius of the base is about |500\ \text{m}.| What should be the ski lift’s length, to the nearest metre?
-
Identify the given measurements
Lateral area of the cone (we must work using the same units of measurement as the radius, so it is necessary to convert the units): |A_L=1{.}7\ \text{km}^2=1\ 700\ 000\ \text{m}^2|
The measure of the cone’s radius is: |\color{#3B87CD}{r=500\ \text{m}}| -
Determine the formula to use
Since the question refers to the cone’s lateral area and seeks the measure of the apothem, use this formula: ||A_L = \pi \times \color{#3B87CD}{r} \times \color{#FA7921}{a}|| -
Replace the variables with the given measurements
||1\ 700\ 000 = \pi \times \color{#3B87CD}{500}\times\color{#FA7921}{a}|| -
Isolate the sought variable
||\begin{align}\color{#EC0000}{\dfrac{\color{black}{1\ 700\ 000}}{500}} &= \color{#EC0000}{\dfrac{\color{black}{\pi \times \color{#3B87CD}{500}\times}\color{#FA7921}{a}}{500}}\\ 3\ 400 &= \pi \color{#FA7921}{a}\\ \color{#EC0000}{\dfrac{\color{black}{3\ 400}}{\pi}} &= \color{#EC0000}{\dfrac{\color{black}{\pi}\color{#FA7921}{a}}{\pi} }\\ 1\ 082{.}25\ \text{m} &\approx \color{#FA7921}{a}\end{align}||
Answer: The ski lift should be approximately |1\ 082\ \text{m}.|
Sometimes, the height of a pyramid or cone must be determined from the area even though it is not in the formula for the area. In that case, find the apothem of the solid or the radius of the base. Then, use the Pythagorean Theorem to calculate the height.
Whether for a pyramid or a cone, the procedure is very similar.
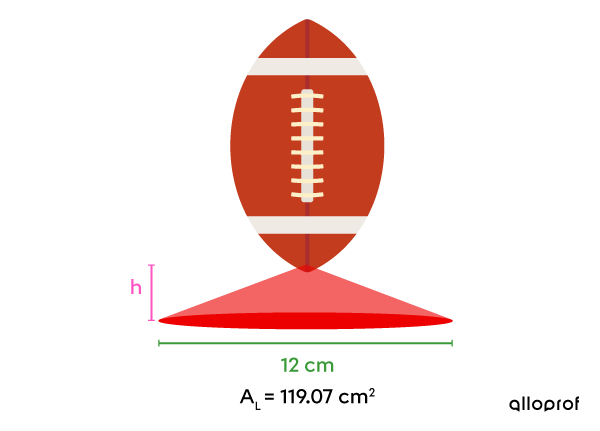
During kickoffs in football games, kickers often use small cone-shaped stands to hold the ball upright.
If the tip of the ball coincides with the apex of the cone, how far is the ball from the ground when it is on the stand?
-
Identify the given measurements
Lateral area of the cone: |A_L=119{.}07\ \text{cm}^2|
Measure of the cone’s radius: |\color{#3A9A38}{r}=\dfrac{12}{2}=\color{#3A9A38}{6\ \text{cm}}| -
Determine the formula to use
Since the lateral area of the cone is known, its height cannot directly be found. Determine the cone’s apothem using the following formula. ||A_L = \pi \times \color{#3A9A38}{r} \times \color{#FA7921}{a}|| -
Replace the variables with the given measurements
||119{.}07 = \pi \times \color{#3A9A38}{6} \times \color{#FA7921}{a}|| -
Isolate the sought variable
||\begin{align} \color{#EC0000}{\dfrac{\color{black}{119{.}07}}{6}} &=\color{#EC0000}{\dfrac{\color{black}{\pi \times \color{#3A9A38}{6} \times \color{#FA7921}{a}}}{6}}\\19{.}845 &= \pi \color{#FA7921}{a}\\\color{#EC0000}{\dfrac{\color{black}{19{.}845}}{\pi}} &=\color{#EC0000}{\dfrac{\color{black}{\pi} \color{#FA7921}{a}}{\pi}}\\ 6{.}32\ \text{cm} &\approx \color{#FA7921}{a}\end{align}||
As shown in the image below, to find the cone’s height, form a right triangle bounded by its height, apothem, and half of its base. Then, apply the Pythagorean Theorem.

||\begin{align} \color{#FF55C3}{a}^2 + \color{#3A9A38}{b}^2 &= \color{#FA7921}{c}^2\\\\ \color{#FF55C3}{h}^2 + \color{#3A9A38}{6}^2 &= \color{#FA7921}{6{.}32}^2\\ \color{#FF55C3}{h}^2 + 36 &\approx 39{.}94\\ \color{#FF55C3}{h}^2 + 36 \color{#ec0000}{-36} &\approx 39{.}94 \color{#EC0000}{-36} \\ \color{#FF55C3}{h}^2 &\approx 3{.}94 \\ \color{#EC0000}{\sqrt{\color{#FF55C3}{h}^\color{black}{2}}} &\approx \color{#EC0000}{\sqrt{\color{black}{3{.}94}}}\\ \color{#FF55C3}{h} &\approx 1{.}98\ \text{cm}\end{align}||
Answer: The ball is approximately |1{.}98\ \text{cm}| off the ground.
The previous example demonstrates that it is usually necessary to find the measure of the apothem before determining the height using the Pythagorean Theorem. Finding the height of a cone or pyramid from its area requires a few more calculations than simply calculating the measure of the apothem.
If, instead of the lateral area, we are given the volume of a cone or a pyramid and the dimensions of the base, the height can be found directly. This measurement is in the formula for the volume of cones and pyramids. The formula for the volume of these solids is |V= \dfrac{A_b \times h}{3}.|
To find the apothem of one of these solids from the volume, first find the height. Then, use the Pythagorean Theorem to calculate the apothem. Read the concept sheet about finding the measurement of the apothem of a pyramid or a cone for more information.
What is the height of a traditional billiard ball (in millimetres)?

-
Identify the given measurements
Total area of the billiard ball: |A_T=10\ 273{.}58 \ \text{mm}^2| -
Determine the formula to use
Since the question refers to the area of a sphere, use the following formula: ||A = 4 \pi r^2|| -
Replace the variables with the given measurements
||10 \ 273{.}58 = 4 \pi r^2|| -
Isolate the sought variable
||\begin{align} \color{#EC0000}{\dfrac{\color{black}{10 \ 273{.}58}}{4\pi}} &= \color{#EC0000}{\dfrac{\color{black}{4 \pi r^2}}{4\pi}}\\ 817{.}55 &\approx r^2\\ \color{#EC0000}{\sqrt{\color{black}{817{.}55}}} &\approx \color{#EC0000}{\sqrt{\color{black}{r^2}}} \\28{.}59\ \text{mm} &\approx r \end{align}||
Since the height of a sphere is equivalent to twice the radius, |\color{#3A9A38}{h}= 28{.}59 \times 2 = 57{.}18 \ \text{mm}.|

Answer: The height of the billiard ball is |57{.}18 \ \text{mm}.|
Pour valider ta compréhension à propos des mesures manquantes dans les solides de façon interactive, consulte la MiniRécup suivante :
