Calorimetry is used to experimentally determine the amounts of heat involved in a transformation.
The law of conservation of energy states that energy can neither be created nor destroyed. Instead, it changes shape indefinitely, as it is transformed by energy transfers. In chemistry, energy transfers generally take the form of the release or absorption of heat. Two principles are important in calorimetry:
-
During a transfer, heat always travels from the hottest to the coldest.
-
To measure the energy involved, it is necessary to use an isolated system.
Left: An open system allows energy and matter to be exchanged with the surrounding environment.
Centre: A closed system allows energy to be exchanged with the surrounding environment, but no matter can be exchanged.
Right: An isolated system allows no exchange of matter or energy with the environment.

For a given reaction, we can then relate the thermal energy, specific heat capacity, mass and temperature variation of a substance.
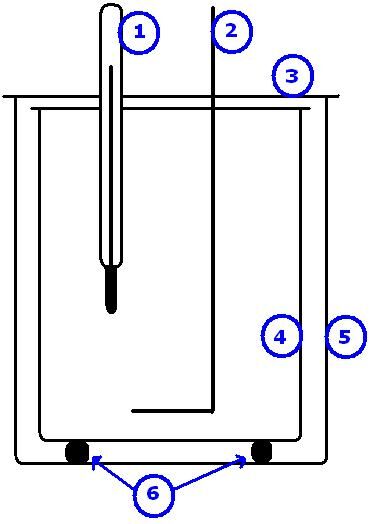
A calorimeter is an isolated system used to take the measurements needed to perform calorimetric calculations.
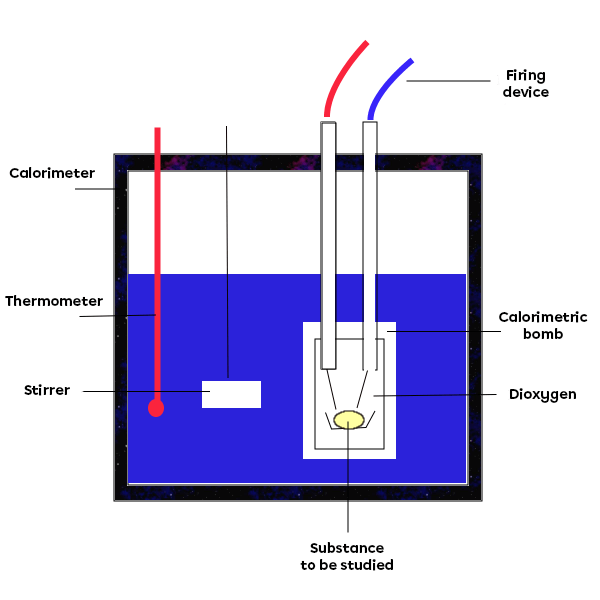
A calorimeter is used to experimentally determine the amounts of energy transferred during a transformation. There are several types of calorimeter, depending on the type of transformation being studied. In the case of a reaction taking place in an aqueous environment, the transformation takes place in the reservoir of the calorimeter, directly in the water. In other cases, a calorimetric bomb is used to determine the energy involved in a combustion reaction, for example.
Left: diagram of a calorimeter used to study a reaction taking place in an aqueous environment (1-thermometer; 2-agitator; 3-cover; 4-inner wall of the calorimeter; 5-outer wall of the calorimeter; 6-insulators). Right: diagram of a calorimetric bomb used to study a reaction taking place in ambient air.
Once the substances have been added to the calorimeter and sealed, the thermal agitation of the particles involved in the reaction can be transmitted to the water in the calorimeter. The temperature of the water is measured during the reaction. If the chemical reaction generates heat, the water temperature rises. If, on the other hand, the reaction is endothermic, the water cools as it transfers part of its thermal energy to the reaction. This measurement of the variation in temperature in an isolated system will make it possible to determine the energy involved in the transfer using the formula Q = m c ΔT.
In the laboratory, a simple way to build a calorimeter is to use two polystyrene cups stacked one on top of the other, a plastic lid and a thermometer. The advantage of polystyrene is that it takes very little part in heat exchange. This means that the material of the calorimeter has no influence on heat transfer, and heat exchange can be considered as taking place entirely with the water in the calorimeter.
The specific heat capacity of a substance, designated by the letter c, is a characteristic property. It gives the precise capacity of this substance to absorb or give off heat.
In other words, the specific heat capacity is the amount of heat that 1 gram of a substance must absorb for its temperature to rise by 1 degree Celsius. It can also be the amount of heat that 1 gram of the substance must lose for its temperature to drop by 1 degree Celsius.
The unit of measurement for specific heat capacity is J/(g⋅°C).
Since it is a characteristic property, the specific heat capacity is unique to each substance. The higher the specific heat capacity of a substance, the more it needs to be heated to increase its temperature. Conversely, a substance with a low specific heat capacity heats up quickly, but cools down just as quickly.
The specific heat capacity of water is 4.19 J/(g⋅°C), while that of ethylene glycol is 2.20 J/(g⋅°C). This means that for the same mass, the water needs to be heated more to achieve the same temperature increase.
For a table of the specific heat capacities of different substances, see this concept sheet: Specific Heat Capacity of Some Substances
The heat of a reaction is proportional to the mass of the substance involved, the temperature difference observed and the nature of the substance. To calculate the amount of energy transferred or released in the form of heat, we use the following relationship:
|Q=m\,c\,\Delta T|
where
|Q| represents the amount of energy transferred in joules (J)
|m| represents the mass of the substance in grams (g)
|c| represents the heat capacity of the substance in J/(g·°C)
|\Delta T| represents the variation in temperature |\left(T_{\text{final}} - T_{\text{initial}} \right)| in °C
Note that this formula applies to only one substance at a time. However, since energy (Q) is conserved during transfers, we can consider the following relationship:
|-Q_{\text{released}}= +Q_{\text{absorbed}}|
By convention, a negative energy value (-Q) is considered to be the energy released, whereas a positive energy value (+Q) corresponds to the energy absorbed.
When the temperature variation is positive, this means that the substance has absorbed heat during the transfer. Conversely, when the temperature variation is negative, the substance has released heat into its environment or transferred it to another substance.
A beaker containing 800 g of water is heated on a hot plate. If the water temperature rises from 20°C to 85°C, how much energy has the water absorbed?
-
Problem data or values ||\begin{align}Q &= x\\ m &= 800\ \text{g}\\ c &= 4.19\ \text{J/(g}\cdot ^{\circ}\!\!C)\\ \Delta T &= 85\ ^{\circ}\!C - 20\ ^{\circ}\!C = 65\ ^{\circ}\!C\end{align}||
-
Energy calculation ||\begin{align}Q &= m\,c\,\Delta T\\ Q &= 800\ \text{g}\times 4.19\ \text{J/(g}\cdot ^{\circ}\!\!C) \times 65\ ^{\circ}\!C\\ Q &= 217\ 880\ \text{J}\end{align}||
The energy absorbed by the water is |217\ 880\ \text{J}.|
To calculate the energy transferred between two systems, it is assumed that the heat given by the first system is equal to the heat received by the second system. We can therefore consider the following relationship:
|-Q_{1}=Q_{2}|
where
|-m_{1}c_{1}\Delta T_{1} = m_{2} c_{2}\Delta T_{2}|
Finally, we use the relationship below for an energy transfer for the same substance with different amounts of mass (or volume) and different temperatures.
|m_{1}T_{1} +m_{2}T_{2} = m_{\text{tot}}T_{\text{tot}}|
Subscripts 1 are associated with one substance (for example, one with a high temperature).
Subscripts 2 are associated with a second substance (for example, one with a low temperature).
|m_{\text{tot}}| is the total mass of the 2 substances.
|T_{\text{tot}}| is the average temperature (average of the other 2 temperatures).
Mix 100 mL of cold water with 150 mL of hot water. The temperature of the mixture is measured and the thermometer indicates 25°C. Given that the initial temperature of the cold water was 7.5°C, what was the initial temperature of the hot water?
-
Problem data or values
|m_{1}| (cold water) |= 100\ \text{ g}| (|1\ \text{mL}| is equivalent to |1\text{ g}| of water)
|m_{2}| (hot water) |= 150\text{ g}|
|m_{\text{tot}} = 100\text{ g} + 150\text{ g} = 250\text{ g}|
|T_{1}| (cold water) |= 7.5^\circ C|
|T_{2}| (hot water) |=| ?
|T_{\text{tot}}= 25^\circ C|
-
Calculating the hot water temperature ||\begin{align}m_{1} T_{1} +m_{2} T_{2} &= m_{\text{tot}} T_{\text{tot}}\\ 100\text{ g}\times 7.5\ ^{\circ}C +150\text{ g}\times T_{2} &= 250\text{ g}\times 25\ ^{\circ}C\\ 750\text{ g}\cdot^{\,\circ}\!C+150\text{ g}\times T_{2} &= 6\,250\text{ g}\cdot^{\,\circ}\!C\\ 150\text{ g}\times T_{2} &= 5\,500\text{ g}\cdot^{\,\circ}\!C\\ T_{2} &= 36.7\ ^{\circ}C\end{align}||
The initial temperature of the hot water was therefore |36.7\, ^\circ C.|
If the mixture is composed of two different substances, the following formula should be used to calculate the final temperature of the system: ||-m_1c_1(T_f -T_{i1}) = m_2c_2(T_f-T_{i2})||The final temperature of the mixture |(T_f)| can be isolated using various mathematical procedures. This gives the following formula: ||T_{f} = \dfrac {m_{1}c_{1}T_{i1} + m_{2}c_{2}T_{i2}}{m_{1}c_{1}+m_{2}c_{2}}||
To cool 250 mL of hot chocolate to a temperature of 80°C, add 75 mL of milk at 20°C. The specific heat capacity of milk is 3.97 J/(g⋅°C), while that of hot chocolate is the same as that of water. Assuming that the densities of hot chocolate and milk are both equal to that of water (1 g/mL), what will be the final temperature of the mixture?
-
Problem data or values
For hot chocolate :
|m_1 = 250\ \text{g}| (obtained from the mass density and volume)
|c_1 = 4.19\ \text{J/(g}\cdot\,^\circ C)|
|T_{i1} = 80\, ^\circ C|
For milk :
|m_2 = 75\ \text{g}| (obtained from the mass density and volume)
|c_2 = 3.97\ \text{J/(g}\cdot\, ^\circ C)|
|T_{i2} = 20\,^\circ C|
-
Calculating the final temperature of the mixture ||\begin{align}T_{f} &= \dfrac{m_{1}c_{1}T_{i1} + m_{2}c_{2}T_{i2}}{m_{1}c_{1}+m_{2}c_{2}}\\ T_f &= \dfrac{250\ \text{g} \times 4.19\ \text{J/(g}\cdot^{\,\circ}\! C) \times 80\ ^\circ C + 75\ \text{g} \times 3.97\ \text{J/(g}\cdot^{\,\circ}\! C) \times 20\ ^\circ C}{250\ \text{g} \times 4.19\ \text{J/(g}\cdot^{\,\circ}\! C) + 75\ \text{g} \times 3.97\ \text{J/(g}\cdot^{\,\circ}\! C)}\\ T_f &= 66.72\, ^\circ C\end{align}||
The final temperature of the mixture is |66.7\, \circ C.|