La calorimétrie permet de déterminer expérimentalement les quantités de chaleur en cause lors d'une transformation.
La loi de la conservation d'énergie stipule que l'énergie ne peut être ni créée ni détruite. Elle change plutôt de forme indéfiniment, car elle se transforme au gré des transferts d’énergie. En chimie, les transferts d'énergie s'effectuent généralement sous forme d'un dégagement ou d'une absorption de chaleur. Deux principes sont importants en calorimétrie :
- Lors d’un transfert, la chaleur se déplace toujours du plus chaud au plus froid.
- Pour mesurer l'énergie impliquée, il est nécessaire d'utiliser un système isolé.
À gauche : Un système ouvert permet des échanges d'énergie et de matière avec le milieu environnant.
Au centre : Un sytème fermé permet des échanges d'énergie avec le milieu environnant, mais aucun échange de matière n'est possible.
À droite : Un sytème isolé ne permet aucun échange avec le milieu, ni de matière ni d'énergie.

Pour une réaction donnée, on pourra alors mettre en relation l'énergie thermique, la capacité thermique massique, la masse et la variation de température d'une substance.
Un calorimètre est un système isolé qui permet de prendre les mesures nécessaires pour effectuer des calculs de calorimétrie.
Afin de déterminer expérimentalement les quantités d'énergie transférées au cours d'une transformation, on se sert d'un calorimètre. Selon le type de transformation étudié, plusieurs types de calorimètre existent. La transformation s'effectue dans le réservoir du calorimètre, directement dans l'eau, lorsqu'il s'agit d'une réaction se déroulant en milieu aqueux. Dans les autres cas, on utilisera plutôt une bombe calorimétrique qui permettra, par exemple, de déterminer l'énergie impliquée dans une réaction de combustion.
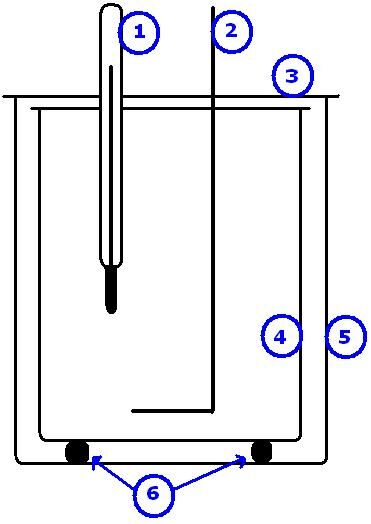
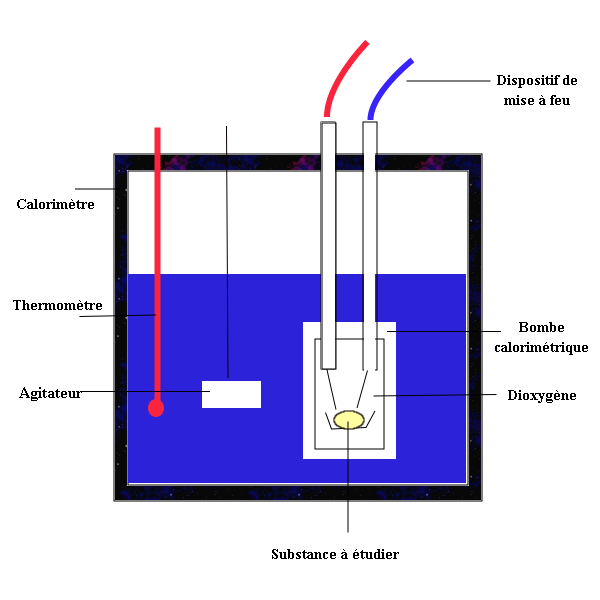
À gauche : schéma d'un calorimètre qui permet d'étudier une réaction se déroulant en milieu aqueux (1-thermomètre; 2-agitateur; 3-couvercle; 4-paroi interne du calorimètre; 5-paroi externe du calorimètre; 6-pieds isolants). À droite: schéma d'un calorimètre à bombe calorimétrique qui permet d'étudier une réaction se déroulant à l'air ambiant.
Après avoir ajouté les substances dans le calorimètre et avoir refermé hermétiquement ce dernier, l'agitation thermique des particules impliquées dans la réaction peut se transmettre à l'eau du calorimètre. Ainsi, pendant la réaction, on mesure la température de l'eau. Si la réaction chimique dégage de la chaleur, la température de l'eau monte. Par contre, s'il s'agit d'une réaction endothermique, l'eau se refroidit, car elle transmet une partie de son énergie thermique à la réaction. Cette mesure de variation de température dans un système isolé permettra de déterminer l'énergie impliquée dans le transfert par la formule (Q = m c ΔT).
En laboratoire, une façon simple de construire un calorimètre est d'utiliser deux verres de polystyrène superposés, un couvercle de plastique et un thermomètre. Le polystyrène offre l'avantage d'être un matériau qui participe très peu aux échanges thermiques. Ainsi, le matériau du calorimètre n'influence pas les transferts de chaleur et on peut considérer que les échanges thermiques sont entièrement effectués avec l'eau du calorimètre.
La capacité thermique massique d’une substance, désignée par la lettre c, est une propriété caractéristique. Elle donne la capacité précise de cette substance d’absorber ou de dégager de la chaleur.
En d’autres mots, la capacité thermique massique est la quantité de chaleur qu’un gramme d'une substance doit absorber pour que sa température s’élève d’un degré Celsius. Il peut s’agir aussi de la quantité de chaleur qu’un gramme de cette substance doit perdre pour que sa température baisse d’un degré Celsius.
L'unité de mesure de la capacité thermique massique est le J/(g·°C).
Étant donné qu'il s'agit d'une propriété caractéristique, la capacité thermique massique est propre à chaque substance. Ainsi, plus la capacité thermique massique d'une substance est élevée, plus il faut la chauffer pour augmenter sa température. Au contraire, une substance ayant une faible capacité thermique massique se réchauffe rapidement, mais elle se refroidit aussi rapidement.
La capacité thermique massique de l'eau est de 4,19 J/(g·°C) alors que celle de l'éthylène glycol est de 2,20 J/(g·°C). Cela signifie qu'à masses égales, il faut davantage chauffer l'eau pour observer la même augmentation de température.
Pour avoir accès au tableau des capacités thermiques massiques massiques de différentes substances, tu peux consulter cette fiche:
La chaleur d'une réaction est proportionnelle à la masse de la substance impliquée ainsi qu'à l'écart de température observé et à la nature de la substance. Ainsi, pour calculer la quantité d’énergie transférée ou dégagée sous forme de chaleur, on utilise la relation suivante :
|Q=m\,c\,\Delta T|
où
|Q| représente la quantité d'énergie transférée en joules (J)
|m| représente la masse de la substance en grammes (g)
|c| représente la capacité thermique de la substance en J/(g·°C)
|\Delta T| représente la variation de température |\left( T_{\text{finale}} - T_{\text{initiale}} \right)| en °C
Il est à noter que cette formule s'emploie pour une seule substance à la fois. Toutefois, puisque l'énergie (Q) se conserve lors des transferts, on peut considérer la relation suivante :
|-Q_{\text{dégagée}}= +Q_{\text{absorbée}}|
Par convention, une valeur d'énergie négative (-Q) est considérée comme de l'énergie dégagée alors qu'une valeur d'énergie positive (+Q) correspond à de l'énergie absorbée.
Lorsque la variation de température est positive, cela signifie que la substance a absorbé de la chaleur au cours du transfert. À l'inverse, lorsque la variation de température est négative, la substance a dégagé de la chaleur dans son environnement ou elle l'a transférée à une autre substance.
Un bécher contenant 800 g d'eau est chauffé sur une plaque chauffante. Si la température de l'eau passe de 20 °C à 85 °C, quelle quantité d'énergie l'eau a-t-elle absorbée?
-
Données du problème ||\begin{align}Q &= x\\ m &= 800\ \text{g}\\ c &= 4{,}19\ \text{J/(g}\cdot ^{\circ}\!\!C)\\ \Delta T &= 85\ ^{\circ}\!C - 20\ ^{\circ}\!C = 65\ ^{\circ}\!C\end{align}||
-
Calcul de l'énergie ||\begin{align}Q &= m\,c\,\Delta T\\ Q &= 800\ \text{g}\times 4{,}19\ \text{J/(g}\cdot ^{\circ}\!\!C) \times 65\ ^{\circ}\!C\\ Q &= 217\ 880\ \text{J}\end{align}||
L'énergie absorbée par l'eau est de |217\ 880\ \text{J}.|
Pour calculer l'énergie transférée entre deux systèmes, on suppose que la chaleur donnée par un premier système est égale à la chaleur reçue par le deuxième système. De ce fait, on peut considérer la relation suivante :
|-Q_{1}=Q_{2}|
où
|-m_{1}c_{1}\Delta T_{1} = m_{2} c_{2}\Delta T_{2}|
Enfin, on utilise la relation ci-dessous lors d’un transfert d’énergie pour une même substance possédant des quantités de masses (ou volumes) et des températures différentes.
|m_{1}T_{1} +m_{2}T_{2} = m_{\text{tot}}T_{\text{tot}}|
Les indices 1 sont associés à une substance (par exemple, celle dont la température est élevée).
Les indices 2 sont associés à une 2e substance (par exemple, celle dont la température est basse).
|m_{\text{tot}}| est la masse totale des 2 substances.
|T_{\text{tot}}| est la température moyenne (moyenne des 2 autres températures).
On mélange 100 mL d’eau froide avec 150 mL d’eau chaude. On mesure la température du mélange obtenu et le thermomètre indique 25 °C. Sachant que la température initiale de l’eau froide était de 7,5 °C, quelle était celle de l’eau chaude au départ?
-
Données du problème
|m_{1}| (eau froide) |= 100\text{ g}| (|1\text{ mL}| est équivalent à |1\text{ g}| d’eau)
|m_{2}| (eau chaude) |= 150\text{ g}|
|m_{tot} = 100\text{ g} + 150\text{ g} = 250\text{ g}|
|T_{1}| (eau froide) |= 7{,}5\ ^\circ C|
|T_{2}| (eau chaude) |=| ?
|T_{tot} = 25\ ^\circ C|
-
Calcul de la température de l'eau chaude ||\begin{align}m_{1} T_{1} +m_{2} T_{2} &= m_{\text{tot}} T_{\text{tot}}\\ 100\text{ g}\times 7{,}5\ ^{\circ}C +150\text{ g}\times T_{2} &= 250\text{ g}\times 25\ ^{\circ}C\\ 750\text{ g}\cdot^{\,\circ}\!C+150\text{ g}\times T_{2} &= 6\,250\text{ g}\cdot^{\,\circ}\!C\\ 150\text{ g}\times T_{2} &= 5\,500\text{ g}\cdot^{\,\circ}\!C\\ T_{2} &= 36{,}7\ ^{\circ}C\end{align}||
La température initiale de l’eau chaude était donc de |36{,}7\ ^\circ C.|
Si le mélange est composé de deux substances différentes, on utilisera plutôt la formule suivante pour calculer la température finale du système : ||-m_1c_1(T_f -T_{i1}) = m_2c_2(T_f-T_{i2})||On peut isoler la température finale du mélange |(T_f)| à l'aide de diverses manipulations mathématiques. On obtient alors la formule suivante : ||T_{f} =\dfrac {m_{1}c_{1}T_{i1} + m_{2}c_{2}T_{i2}}{m_{1}c_{1}+m_{2}c_{2}}||
Afin de refroidir 250 mL de chocolat chaud dont la température est de 80 °C, on y ajoute 75 mL de lait à 20 °C. La capacité thermique massique du lait est de 3,97 J/(g·°C) alors que celle du chocolat chaud est la même que celle de l'eau. Si l'on considère que les masses volumiques du chocolat chaud et du lait sont toutes deux égales à celle de l'eau (1 g/mL), quelle sera la température finale du mélange?
-
Données du problème
Pour le chocolat chaud :
|m_1 = 250\ \text{g}| (obtenue à partir de la masse volumique et du volume)
|c_1 = 4{,}19\ \text{J/(g}\cdot^{\,\circ}\! C)|
|T_{i1} = 80\ ^\circ C|
Pour le lait :
|m_2 = 75\ \text{g}| (obtenue à partir de la masse volumique et du volume)
|c_2 = 3{,}97\ \text{J/(g}\cdot^{\,\circ}\! C)|
|T_{i2} = 20\ ^\circ C|
-
Calcul de la température finale du mélange ||\begin{align}T_{f} &= \dfrac{m_{1}c_{1}T_{i1} + m_{2}c_{2}T_{i2}}{m_{1}c_{1}+m_{2}c_{2}}\\ T_f &= \dfrac{250\ \text{g} \times 4{,}19\ \text{J/(g}\cdot^{\,\circ}\! C) \times 80\ ^\circ C + 75\ \text{g} \times 3{,}97\ \text{J/(g}\cdot^{\,\circ}\! C) \times 20\ ^\circ C}{250\ \text{g} \times 4{,}19\ \text{J/(g}\cdot^{\,\circ}\! C) + 75\ \text{g} \times 3{,}97\ \text{J/(g}\cdot^{\,\circ}\! C)}\\ T_f &= 66{,}72\ ^\circ C\end{align}||
La température finale du mélange est de |66{,}7\ ^\circ C.|