Ordering fractions means to compare them in order to place them in ascending (increasing) or descending (decreasing) order.
To learn more about ascending or descending order, read the Ascending and Descending Order concept sheet.
When the denominators are common (identical), the numerators indicate if one fraction is smaller or larger than another.
The larger numerator indicates a larger fraction because more parts are used. Similarly, the smaller numerator indicates a smaller fraction because fewer parts are used.
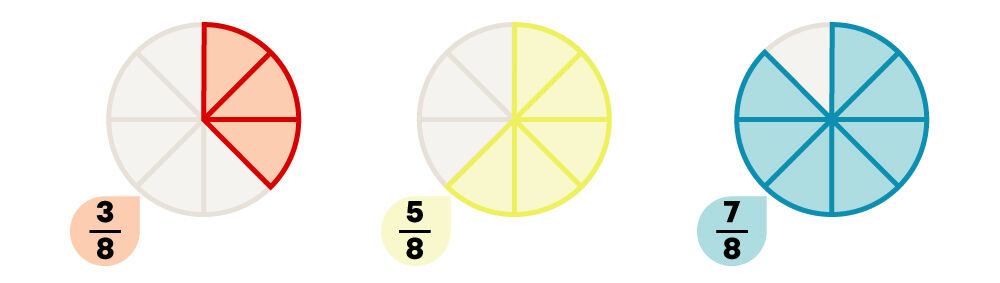
For the fractions |\dfrac{3}{8},| |\dfrac{5}{8}| and |\dfrac{7}{8},| the smallest numerator is |3| and the biggest is |7.| Therefore, the ascending order of these fractions is |\dfrac{3}{8},| |\dfrac{5}{8}| and |\dfrac{7}{8}.|
When the denominators are common (identical), the numerators indicate if one fraction is smaller or larger than another.
The larger numerator indicates a larger fraction because more parts are used. Similarly, the smaller numerator indicates a smaller fraction because fewer parts are used.
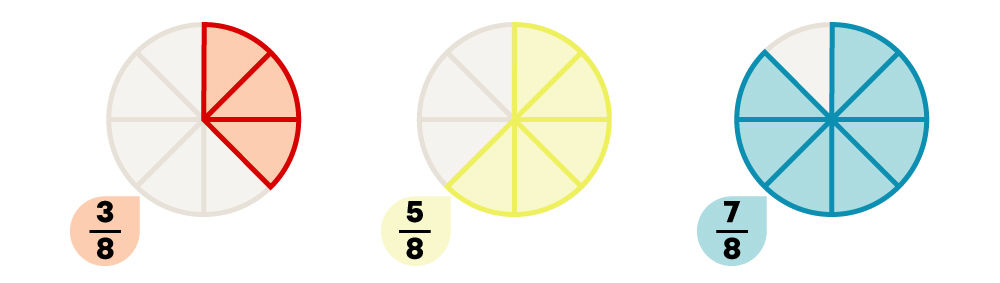
For the fractions |\dfrac{3}{8},| |\dfrac{5}{8}| and |\dfrac{7}{8},| the smallest numerator is |3| and the biggest is |7.| Therefore, the ascending order of these fractions is |\dfrac{3}{8},| |\dfrac{5}{8}| and |\dfrac{7}{8}.|
When the numerators are common (identical), the denominators indicate if one fraction is smaller or larger than another.
The larger denominator indicates the smaller fraction because the whole is divided into smaller parts. Similarly, the smaller denominator indicates the larger fraction because the whole is divided into larger parts.
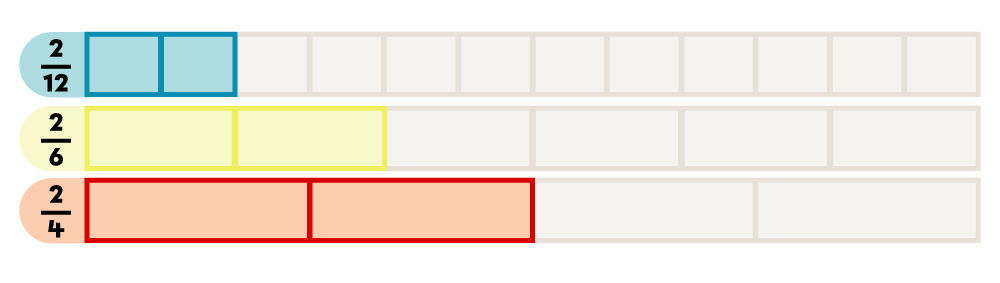
For the fractions |\dfrac{2}{12},| |\dfrac{2}{6}| and |\dfrac{2}{4},| the smallest denominator is |4| and the largest is |12.| Therefore, the ascending order of these fractions is |\dfrac{2}{12},| |\dfrac{2}{6}| and |\dfrac{2}{4}.|
When the numerators and denominators are different, convert the fractions to equivalent fractions with a common denominator.
I have to follow these steps to compare and order fractions with different numerators and denominators.
-
I identify the denominator that is the multiple of the others.
-
For each fraction that needs to be converted, I find out by what number to multiply each denominator to get a common denominator.
-
I multiply the numerator of each fraction by the same number that I used for their denominators.
-
I compare the numerators of the fractions with the common denominators.
-
I write the result using the initial fractions.
Order the fractions |\dfrac{4}{9},| |\dfrac{2}{3}| and |\dfrac{3}{18}| in ascending order.
|
 |
|
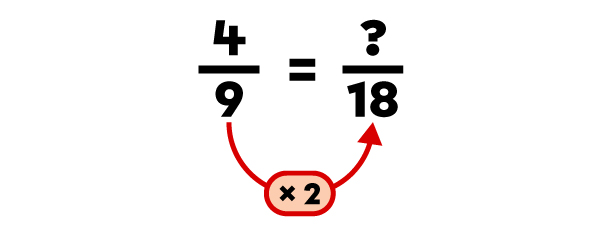
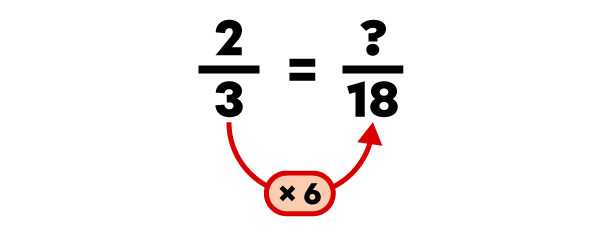 |
|
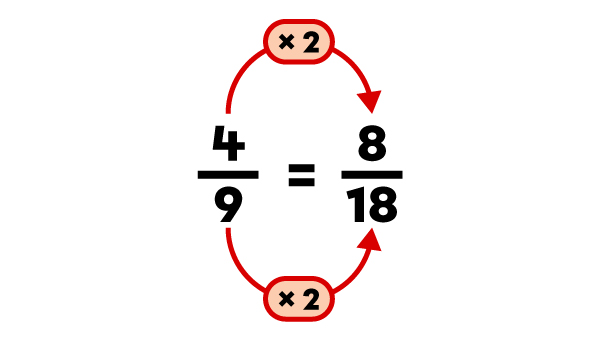
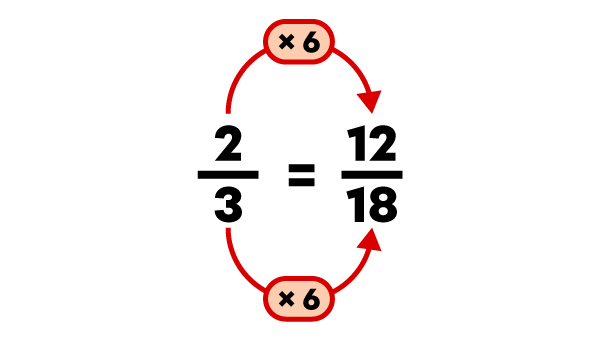 |
|

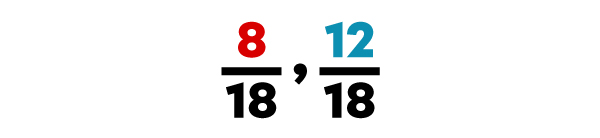 |
|
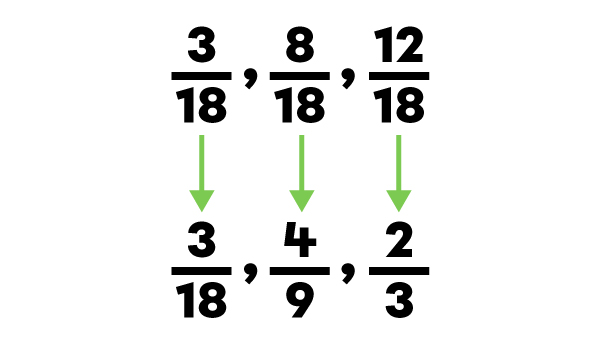 |
The ascending order of the fractions is |\dfrac{3}{18},| |\dfrac{4}{9}| and |\dfrac{2}{3}.|