Ordonner des fractions, c’est les comparer pour pouvoir les placer en ordre croissant ou décroissant.
Pour savoir ce qu’est l’ordre croissant ou décroissant, tu peux lire la fiche L’ordre croissant et décroissant.
Lorsque les dénominateurs sont communs (identiques), ce sont les numérateurs qui permettent de savoir si une fraction est plus petite ou plus grande qu’une autre.
Le plus grand numérateur indique la fraction la plus grande puisqu’un plus grand nombre de parties est utilisé. À l’inverse, le plus petit numérateur indique la fraction la plus petite puisqu’un plus petit nombre de parties est utilisé.
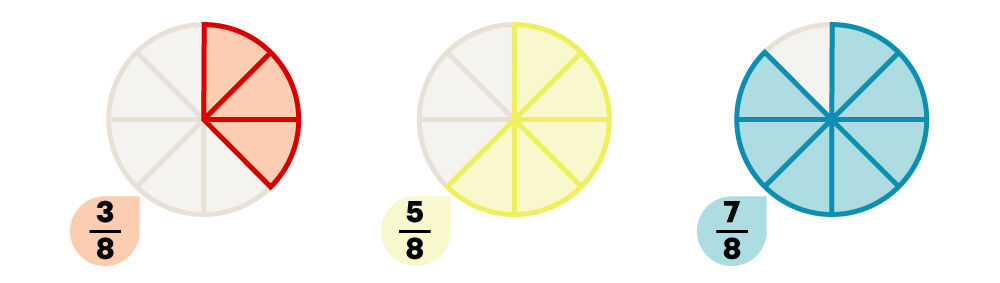
Pour les fractions |\dfrac{3}{8}|, |\dfrac{5}{8}| et |\dfrac{7}{8}|, le plus petit numérateur est |3| et le plus grand est |7|. L’ordre croissant de ces fractions est donc |\dfrac{3}{8}|, |\dfrac{5}{8}| et |\dfrac{7}{8}.|
Lorsque les dénominateurs sont communs (identiques), ce sont les numérateurs qui permettent de savoir si une fraction est plus petite ou plus grande qu’une autre.
Le plus grand numérateur indique la fraction la plus grande puisqu’un plus grand nombre de parties est utilisé. À l’inverse, le plus petit numérateur indique la fraction la plus petite puisqu’un plus petit nombre de parties est utilisé.
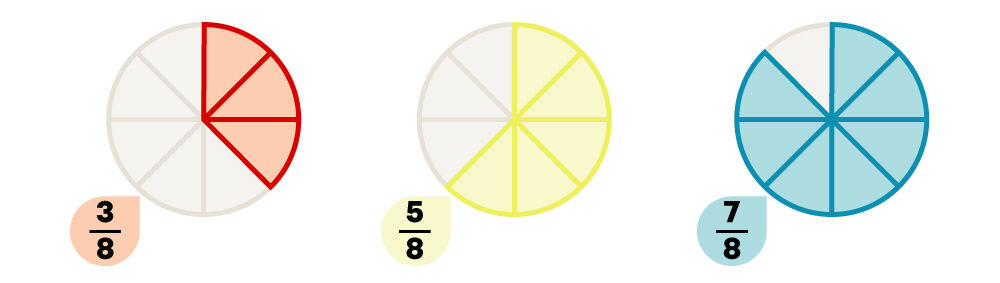
Pour les fractions |\dfrac{3}{8}|, |\dfrac{5}{8}| et |\dfrac{7}{8}|, le plus petit numérateur est |3| et le plus grand est |7|. L’ordre croissant de ces fractions est donc |\dfrac{3}{8}| , |\dfrac{5}{8}| et |\dfrac{7}{8}.|
Lorsque les numérateurs sont communs (identiques), ce sont les dénominateurs qui permettent de savoir si une fraction est plus petite ou plus grande qu’une autre.
Le plus grand dénominateur indique la fraction la plus petite puisque le tout est divisé en morceaux plus petits. À l’inverse, le plus petit dénominateur indique la fraction la plus grande puisque le tout est divisé en morceaux plus gros.
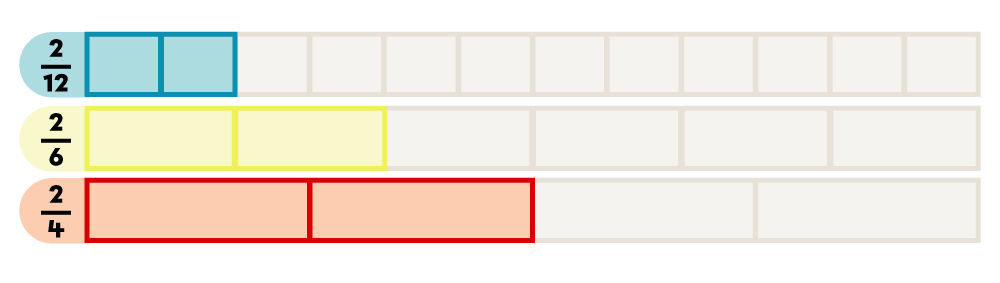
Pour les fractions |\dfrac{2}{12}| , |\dfrac{2}{6}| et |\dfrac{2}{4}| , le plus petit dénominateur est |4| et le plus grand est |12| . L’ordre croissant de ces fractions est donc |\dfrac{2}{12}| , |\dfrac{2}{6}| et |\dfrac{2}{4}| .
Lorsque les numérateurs et les dénominateurs sont différents, il faut transformer les fractions afin de trouver des fractions équivalentes ayant un dénominateur commun.
Pour comparer et ordonner des fractions dont les numérateurs et les dénominateurs sont différents, je dois suivre les étapes suivantes :
-
Je repère le dénominateur qui est le multiple des autres.
-
Pour chaque fraction à transformer, je trouve par quel nombre je peux multiplier le dénominateur pour obtenir un dénominateur commun.
-
Je multiplie le numérateur de chaque fraction à transformer par le même nombre que son dénominateur.
-
Je compare les numérateurs des fractions ayant des dénominateurs communs.
-
J’écris le résultat en utilisant les fractions initiales.
Ordonne les fractions |\dfrac{4}{9}|, |\dfrac{2}{3}| et |\dfrac{3}{18}| en ordre croissant.
|
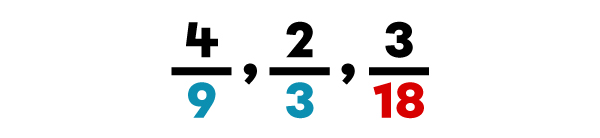
|
|
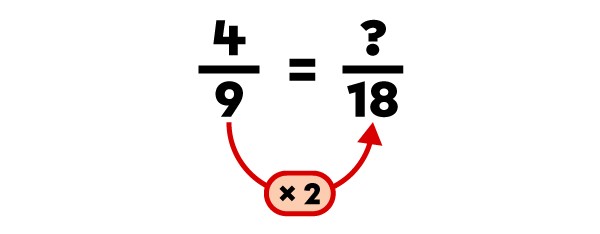
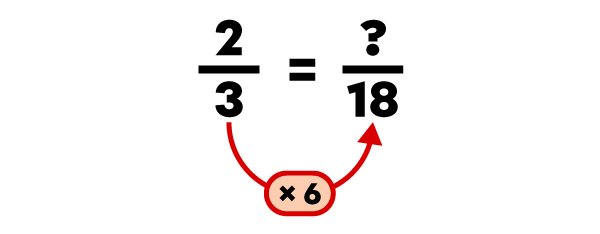 |
|
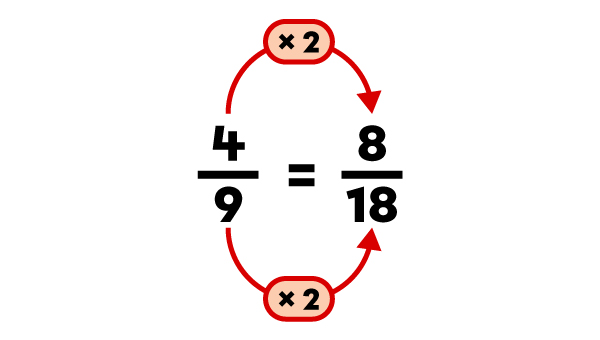
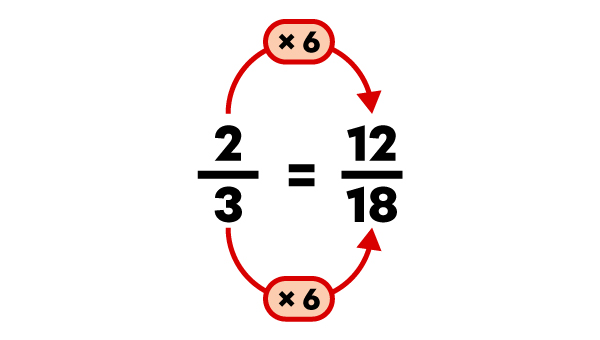 |
|

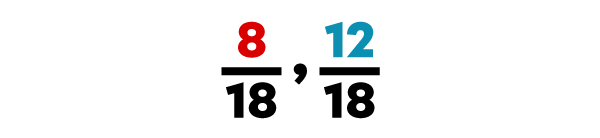 |
|
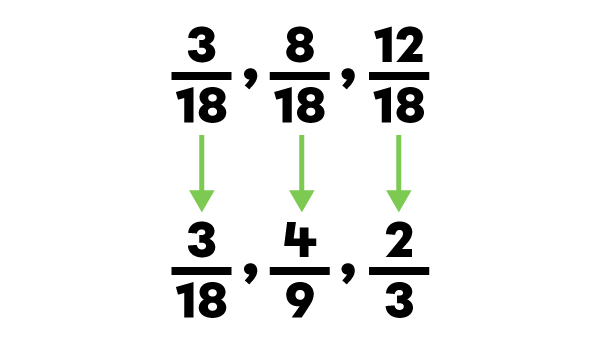
|
L'ordre croissant des fractions est |\dfrac{3}{18}|, |\dfrac{4}{9}| et |\dfrac{2}{3}|.