Ordering Fractions and Mixed Numbers

Which of the following is the greater fraction?
||\dfrac{3}{4}\qquad \qquad \frac{7}{8}||

This situation can be represented using two figures separated into equal parts.

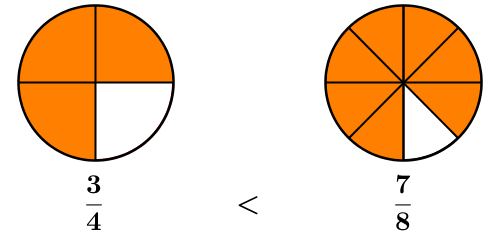
Note that |\dfrac{7}{8}| is greater than |\dfrac{3}{4}.| To prove it, ensure that both fractions have the same denominator, then compare the numerators. The result is the following.

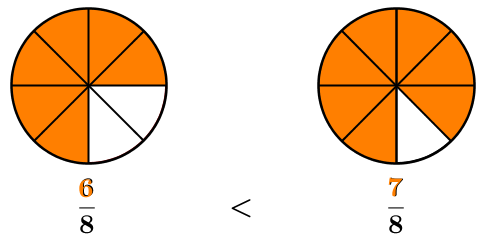
Once they have the same denominator, the greater fraction is the one with the larger numerator.

Which mixed number is greater? ||1\dfrac{2}{3}\qquad \qquad 1\dfrac{3}{4}||

This situation can be represented using the following figures.

Note that |1\dfrac{3}{4}| is greater than |1\dfrac{2}{3}.| To prove it, ensure that the fraction part of each mixed number is over the same denominator.

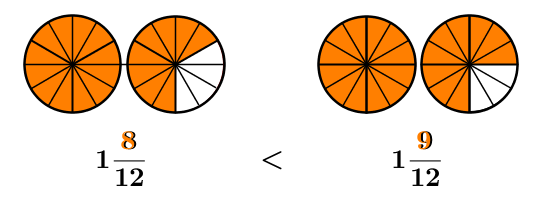
When comparing two mixed numbers with the same integer part, only the fractional part needs to be compared. Once the mixed numbers have the same denominator, the greater mixed number is the one with the larger numerator.

If two mixed numbers do not have the same integer part, the greater one is automatically the one that has the larger whole number part. For example:
||\color{red}{1}\dfrac{3}{4}\qquad < \qquad \color{red}{2}\dfrac{3}{4}||

1. Convert mixed numbers into fractions where necessary.

2. Determine the common denominator for all the fractions.

3. Convert the initial fractions into equivalent fractions with the common denominator.

4. Put the fractions in the desired order, relying on the numerators only.

5. Return the fractions to their original form.

To determine the common denominator of all fractions, the LCM method can be used. In fact, the denominators’ LCM becomes their common denominator.

Place the following fractions in ascending order. ||\dfrac{1}{8}\qquad \dfrac{3}{4}\qquad \dfrac{7}{10}\qquad \dfrac{1}{2}||

1. Convert mixed numbers into fractions where necessary
   Since there are no mixed numbers, move on to the next step.

2. Determine the common denominator for all the fractions by finding the LCM
   The LCM is the following. ||{LCM}(8,4,10,2)=40|| The common denominator is |40.|

3. Convert the initial fractions into equivalent fractions with the common denominator
   ||\dfrac{1{\times 5}}{8{\times 5}}=\color{blue}{\dfrac{5}{40}}\qquad \dfrac{3{\times 10}}{4{\times 10}}=\color{green}{\dfrac{30}{40}}\qquad \dfrac{7{\times 4}}{10{\times 4}}=\color{purple}{\dfrac{28}{40}}\qquad \dfrac{1{\times 20}}{2{\times 20}}=\color{grey}{\dfrac{20}{40}}||

4. Put the fractions in the desired order, relying on the numerators only
   The ascending order of the numerators results in the following. ||\color{blue}{\dfrac{5}{40}}\ <\ \color{grey}{\dfrac{20}{40}}\ <\ \color{purple}{\dfrac{28}{40}}\ <\ \color{green}{\dfrac{30}{40}}||

5. Return the fractions to their original form
   By returning the fractions to their initial form, the desired order is obtained. ||\dfrac{1}{8}\ <\ \dfrac{1}{2}\ <\ \dfrac{7}{10}\ <\ \dfrac{3}{4}||

Place the following rational numbers in descending order. ||1\dfrac{1}{3}\qquad -\dfrac{1}{2}\qquad -\dfrac{5}{6}\qquad \dfrac{13}{12}||

1. Convert mixed numbers into fractions where necessary
   Converting |1\dfrac{1}{3}| into a fraction gives this result. ||1\dfrac{1}{3}\Rightarrow \dfrac{4}{3}||

2. Determine the common denominator for all the fractions by finding the LCM
   The |LCM| of the denominators is the following. ||{LCM}(3,2,6,12)=12|| The common denominator is |12.|

3. Convert the initial fractions into equivalent fractions with the common denominator
   ||\dfrac{4{\times 4}}{3{\times 4}}=\color{blue}{\dfrac{16}{12}}\qquad -\dfrac{1{\times 6}}{2{\times 6}}=\color{green}-\dfrac{6}{12}\qquad -\dfrac{5{\times 2}}{6{\times 2}}=\color{purple}-\dfrac{10}{12}\qquad \dfrac{13}{12}=\color{grey}{\dfrac{13}{12}}||

4. Put the fractions in the desired order, relying on the numerators only
   Placing these fractions in order means placing their numerators in order. To do this, we proceed as we do for integers. Therefore, the decreasing order is the following. ||\color{blue}{\dfrac{16}{12}}\ >\ \color{grey}{\dfrac{13}{12}}\ >\ \color{green}{-\dfrac{6}{12}}\ >\ \color{purple}{-\dfrac{10}{12}}||

5. Return the fractions to their original form
   ||1\dfrac{1}{3}\ >\ \dfrac{13}{12}\ >\ -\dfrac{1}{2}\ >\ -\dfrac{5}{6}||

To place a fraction on a number line, the line must be divided into as many equal parts as the fraction's denominator.

For example, consider the fraction |\dfrac{2}{3}.| The fraction is between |0| and |1.| Since the denominator of the fraction is |3,| we will have to divide the space between |0| and |1| into |3| equal parts.

The fractions’ numerator will then indicate its position on the number line.

If there is an improper fraction (fraction bigger than |1|), divide each whole unit as necessary on the number line. Consider the fraction |\frac{5}{4}.| Because the denominator is |4,| each whole unit on the number line is divided into |4| equal parts. Next, use the numerator to indicate its place on the number line.

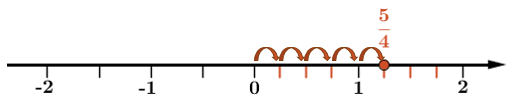
In the case of a mixed number, proceed in much the same way. However, instead of starting from |0,| start from the integer part of the mixed number.

For the mixed number |3\dfrac{1}{2},| divide the space between |3| and |4| into two equal parts.

The procedure is similar for negative fractions and negative mixed numbers.

1. Place each of the numbers expressed in fractional notation on a number line.

2. Place the numbers in the desired order, knowing that the further to the right a number is, the greater it is.

Place the following rational numbers in ascending order.
||\dfrac{9}{5}\qquad \dfrac{1}{2}\qquad 2\dfrac{1}{3}\qquad \dfrac{3}{4}||

1. Place each of the numbers expressed in fractional notation on a number line
   By properly dividing the number line, the numbers can be positioned as follows.

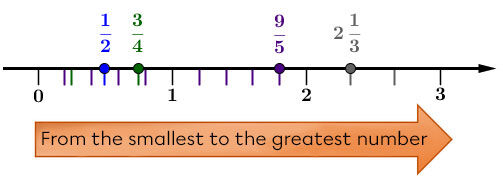
2. Place the numbers in the desired order, knowing that the further a number is to the right, the greater it is
   The result is the following ascending order.
   ||\dfrac{1}{2}\ <\ \dfrac{3}{4}\ <\ \dfrac{9}{5}\ <\ 2\dfrac{1}{3}||