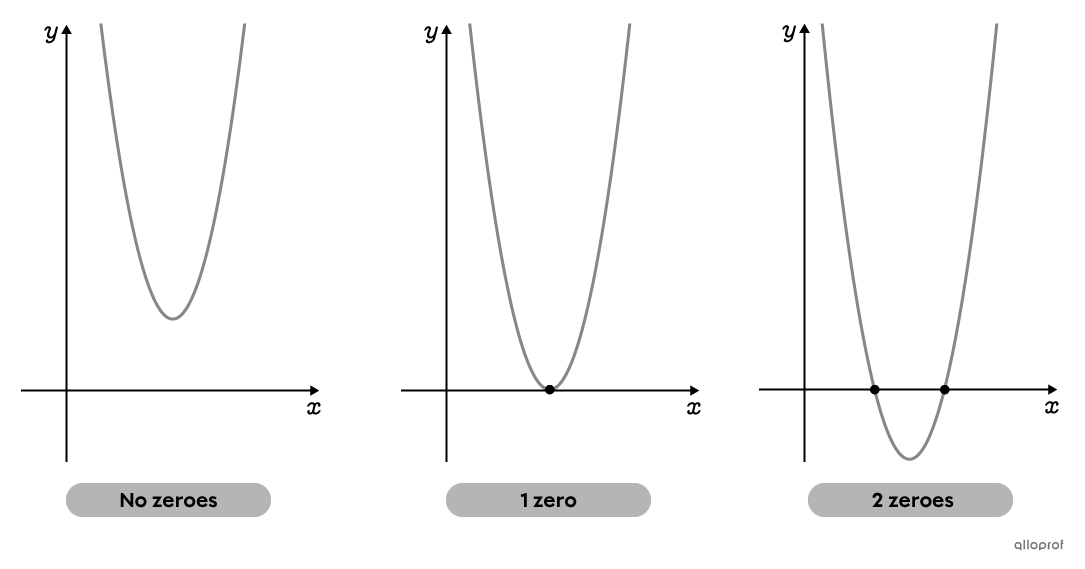
The zero, or |x|-intercept, of a function |f| is a value of |x| for which |f(x)=0.| A function can have multiple zeroes.
Finding the zeroes of a quadratic function amounts to finding the point or points of intersection between the parabola and the |x|-axis. There may be 1, 2, or none.
Find the zeroes of a quadratic function in general form using the following methods.
Find the zeroes of a quadratic function in standard form using the following methods.
Find the zeroes of a quadratic function in factored form using the following methods.
To find the zero or zeroes of a quadratic function in general form |f(x)=ax^2+bx+c,| replace |f(x)| with |0| and find the |x| values that make the equation true. To do this, factor the equation or use the quadratic formula.
Note that |x| cannot be directly isolated in the equation |0=ax^2+bx+c|, because variable |x| is found in 2 terms that are not like terms.
The zero product rule must be applied when factoring to determine the zeroes of a quadratic function.
The zero product rule is as follows.
A product of factors is zero if and only if at least one of its factors is zero.
||a \times b = 0\\ \Updownarrow\\a=0\ \ \text{or}\ \ b=0||
-
Replace |f(x)| with |0.|
-
Factor the polynomial.
-
Apply the zero product rule.
The following example shows when zeroes are determined using a perfect square trinomial.
Determine the zeroes of the function |f(x)=4x^2+12x+9.|
-
Replace |f(x)| with |0|
||\begin{align}f(x)&=4x^2+12x+9\\0&=4x^2+12x+9\end{align}|| -
Factor the polynomial
This polynomial is a perfect square trinomial. This gives the following equation.
||\begin{align} 0&=4x^2+12x+9\\ &=(2x+3)^2\end{align}||So, we have |0=(2x+3)^2| or |0=(2x+3)(2x+3).| -
Apply the zero product rule
Since the 2 factors are identical, the function has only one zero.
||\begin{align}2x+3&=0\qquad\\ 2x&=-3\\x&=-\dfrac{3}{2}\end{align}||
Answer: The zero of the function is |-\dfrac{3}{2}.|
The following example shows when zeroes are determined by completing the square.
Determine the zeroes of the function |f(x)=x^2-0.8x-3.84.|
-
Replace |f(x)| with |0|
||\begin{align}f(x)&=x^2-0.8x-3.84\\0&=x^2-0.8x-3.84\end{align}|| -
Factor the polynomial
||\begin{align}&x^2-0.8x-3.84\\=\ &(x^2-0.8x\color{#3a9a38}{+0.16})-3.84\color{#3a9a38}{-0.16}\\=\ &(x-0.4)^2-4\\=\ &\big((x-0.4)+2\big)\big((x-0.4)-2 \big)\\=\ &(x+1.6)(x-2.4) \end{align}||Therefore, |0=(x+1.6)(x-2.4).| -
Apply the zero product rule
||\begin{aligned}x+1.6&=0\\ x_1&=-1.6\end{aligned}\qquad \begin{aligned}x-2.4&=0\\ x_2&=2.4\end{aligned}||
Answer: The 2 zeroes of the function are |-1.6| and |2.4.|
The following example shows when zeroes are determined using the product-sum technique.
Determine the zeroes of the function |f(x)=x^2-3x-10.|
-
Replace |f(x)| with |0|
||\begin{align}f(x)&=x^2-3x-10\\0&=x^2-3x-10\end{align}|| -
Factor the polynomial
The polynomial is factored with the product-sum technique. We are looking for 2 numbers, |m| and |n,| where the product |m \times n| must be equal to |-10| and the sum |m+n| must be equal to |-3.| Looking at the different factors of |-10,| there is |\color{#3b87cd}m=\color{#3b87cd}{-5}| and |\color{#3b87cd}n=\color{#3b87cd}{2}.|
Next, complete the factorization. ||\begin{align}&x^2-3x-10\\=x^2\color{#3b87cd}{-5}x+\color{#3b87cd}2x-10 \\=x(x-5) + 2(x-5)\\=(x-5)(x+2)\end{align}||So, the result is |0=(x-5)(x +2).| -
Apply the zero product rule
Check for which values of |x| each factor is |0.| ||\begin{aligned}x-5&=0\\x_1&=5\end{aligned}\qquad \begin{aligned}x+2&=0\\x_2&=-2\end {aligned}||
Answer: The 2 zeroes of the function are |-2| and |5.|
It is also possible to use the quadratic formula when the function is given in general form. Here's how.
-
Replace |f(x)| with |0.|
-
Determine the value of |a,| |b,| and |c.|
-
Apply the quadratic formula.
The following example was previously solved by factoring, but this time the quadratic formula will be used.
Determine the zeroes of the function |f(x)=x^2-3x-10.|
-
Replace |f(x)| with |0|
||\begin{align}f(x)&=x^2-3x-10\\0&=\color{#ec0000}1x^2\color{#3b87cd}{-3}x\color{#3a9a38}{-10}\end{align}|| -
Determine the value of |a,| |b,| and |c|
||\color{#ec0000}a=\color{#ec0000}1,\ \color{#3b87cd}b=\color{#3b87cd}{-3}, \ \color{#3a9a38}c=\color{#3a9a38}{-10}|| -
Apply the quadratic formula
||\begin{align}x_{1,2} &= \dfrac{-\color{#3b87cd}b \pm \sqrt{\color{#3b87cd}b^2-4\color{#ec0000}a\color{#3a9a38}c}}{2\color{#ec0000}a}\\\\ &= \dfrac{-(\color{#3b87cd}{-3}) \pm \sqrt{(\color{#3b87cd}{-3})^2-4(\color{#ec0000}1)(\color{#3a9a38}{-10})}}{2(\color{#ec0000}1)} \\ &= \dfrac{3 \pm \sqrt{9 + 40}}{2}\\ &= \dfrac{3 \pm \sqrt{49}}{2}\\&= \dfrac{3 \pm 7}{2} \end{align}||
Next, separate the formula into 2 parts, one using |+| and the other using |-.|
||\begin{aligned} x_1 &= \dfrac{3 + 7}{2}\\&=5 \end{aligned}\qquad\begin{aligned}x_2 &= \dfrac{3 - 7}{2}\\&=-2\end{aligned}||
Answer: The 2 zeroes of the function are |-2| and |5.| This is the same answer obtained before by factoring.
The following example shows when the zeroes are not integers.
Determine the zeroes of the function |f(x)=2x^2+3x-4.|
-
Replace |f(x)| with |0|
||\begin{align}f(x)&=2x^2+3x-4\\0&=2x^2+3x-4\end{align}|| -
Determine the value of |a,| |b,| and |c|
||a=2,\ b=3,\ c=-4|| -
Apply the quadratic formula
||\begin{align}x_{1,2} &= \dfrac{-b \pm \sqrt{b^2-4ac}}{2a}\\\\ &= \dfrac{-3 \pm \sqrt{3^2-4(2)(-4)}}{2(2)} \\ &= \dfrac{-3 \pm \sqrt{9+32}}{4}\\ &= \dfrac{-3 \pm \sqrt{41}}{4}\end{align}||
Because |41| is not a square number, keep the square root and separate the formula into 2 parts, one using |+| and the other using |-.|
||\begin{aligned} x_1 &=\dfrac{-3 + \sqrt{41}}{4}\\&\approx0.85 \end{aligned}\qquad\begin{aligned}x_2 &=\dfrac{-3 - \sqrt{41}}{4}\\&\approx -2.35\end{aligned}||
Answer: The zeroes are |\approx 0.85| and |\approx -2.35.| For a more precise answer, keep the radical.
||\begin{align}x_1 &= \dfrac{-3 + \sqrt{41}}{4}\\ x_2&=\dfrac{-3 - \sqrt{41}}{4}\end{align}||
The following is an example of where the function has no zeroes.
Determine the zeroes of the function |f(x)=-6x^2+2x-3.|
-
Replace |f(x)| with |0|
||\begin{align}f(x)&=-6x^2+2x-3\\0&=-6x^2+2x-3\end{align}|| -
Determine the value of |a,| |b,| and |c|
||a=-6,\ b=2,\ c=-3|| -
Apply the quadratic formula
||\begin{align}x_{1,2} &= \dfrac{-b \pm \sqrt{b^2-4ac}}{2a}\\\\ &= \dfrac{-2 \pm \sqrt{(2)^2-4(-6)(-3)}}{2(-6)} \\ &= \dfrac{-2 \pm \sqrt{4-72}}{-12}\\ &= \dfrac{-2 \pm \sqrt{\color{#EC0000}{-68}}}{-12} \end{align}||
We cannot continue solving the equation, because the number under the square root is negative. The function has no zero.
Answer: The function does not have any zeroes.
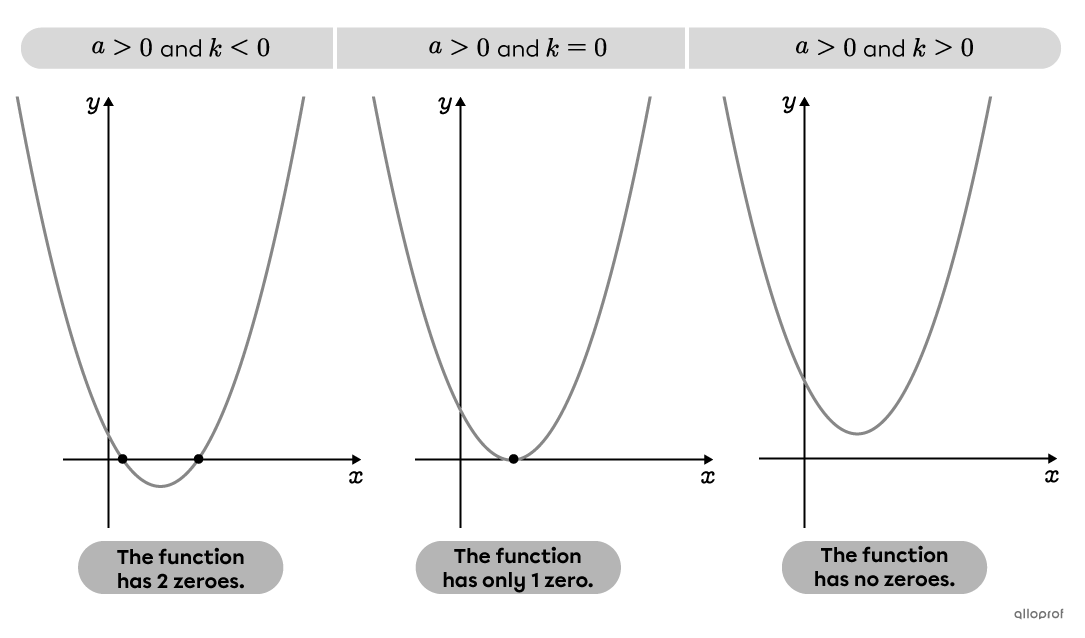
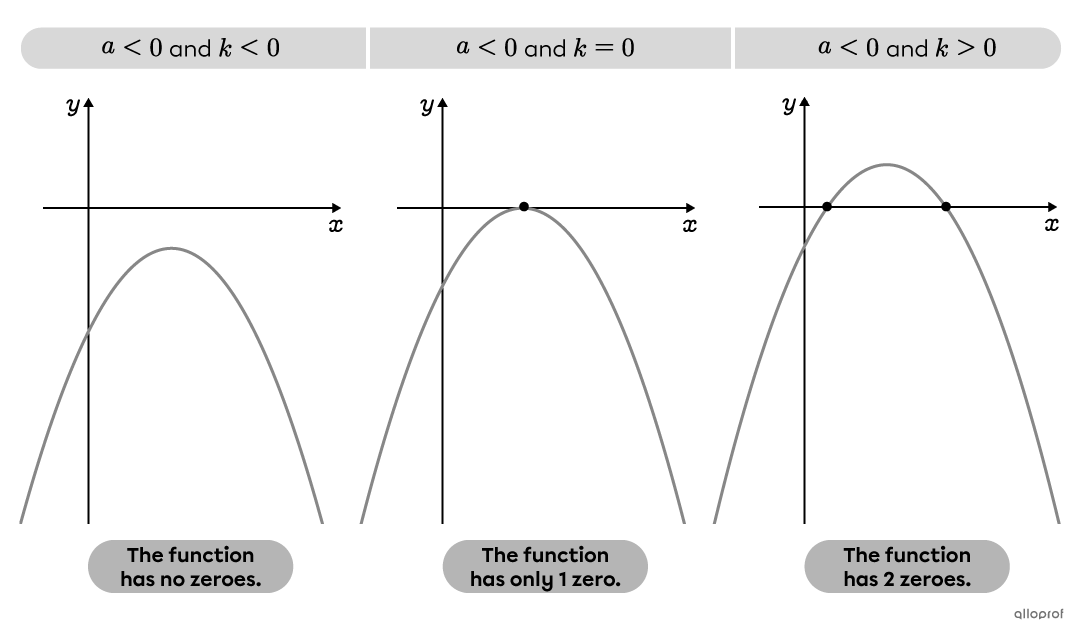
The number of zeroes in a quadratic function can be determined by analysing the discriminant in the quadratic formula.
-
When |b^2-4ac>0,| the function has 2 zeroes.
-
When |b^2-4ac=0,| the function has 1 zero.
-
When |b^2-4ac<0,| the function has no zeroes.
To find the zeroes of a quadratic function in standard form |f(x)=a(x-h)^2+k,| replace |f(x)| by |0,| and then find the |x| value(s) that make the equation true. Isolate |x| directly in the equation or use the zeroes of a function formula for standard form.
When the rule of a quadratic function is in standard form, solve the equation to find the zero(es). Here's how.
-
Replace |f(x)| with |0.|
-
Isolate the brackets.
-
Take the square root of the 2 sides of the equality.
-
Solve the equations.
There are 2 answers when you take the square root of a number: a positive one and a negative.
Determine the zeroes of the function |f(x)=-3(x+5)^2+12.|
-
Replace |f(x)| with |0|
||\begin{align}f(x)&=-3(x+5)^2+12\\ 0&=-3(x+5)^2+12\end{align}|| -
Isolate the brackets
||\begin{align}-12&=-3(x+5)^2\\4&=(x+5)^2\end{align}|| -
Take the square root
||\begin{align}\color{#ec0000}{\sqrt{\color{black}4}}&=\color{#ec0000}{\sqrt{\color{black}{(x+5)^2}}}\\ \pm\ 2&=x+5\end{align}|| -
Solve the equations
||\begin{aligned}-2&=x+5\\-7&=x_1 \end{aligned} \qquad \begin{aligned} 2&=x+5\\-3&=x_2\end{aligned}||
Answer: The 2 zeroes of the function are |-7| and |-3.|
The following is an example of where the function has no zeroes.
Determine the zeroes of the function |f(x)=2(x-1)^2+6.|
-
Replace |f(x)| with |0|
||\begin{align}f(x)&=2(x-1)^2+6\\ 0&=2(x-1)^2+6\end{align}|| -
Isolate the brackets
||\begin{align}-6&=2(x-1)^2\\-3&=(x-1)^2\end{align}|| -
Take the square root
||\begin{align}\color{#ec0000}{\sqrt{\color{black}{-3}}}&=\color{#ec0000}{\sqrt{\color{black}{(x-1)^2}}}\end{align}||
It is impossible to take the square root of a negative number. So, stop solving the problem because the function does not have a zero.
Answer: The function does not have any zeroes.
The number of zeroes possible in a quadratic function in standard form can be determined by analyzing parameters |a| and |k.| The sign of parameter |a| indicates the direction of the parabola’s opening (up or down), while parameter |k| indicates the vertical location of the vertex.
The function in the previous example has no zeroes, since |a>0| and |k>0.|
The zeroes of a function formula can also be used when the function is given in standard form.
Here is the formula for finding the zeroes of a quadratic function in standard form.
||x_{1,2}= h \pm \sqrt{-\dfrac{k}{a}}||
The following example demonstrates the zeroes of a function formula in standard form.
Isolate |x| in the equation |a(x-h)^2+k=0| by performing all the inverse operations.
||\begin{align}a(x-h)^2+k&=0\\
a(x-h)^2+k\color{#ec0000}{-k}&=0\color{#ec0000}{-k}\\
\color{#ec0000}{\dfrac{\color{black}{a(x-h)^2}}{a}}&=\color{#ec0000}{\dfrac{\color{black}{-k}}{a}}\\
\color{#ec0000}{\sqrt{\color{black}{(x-h)^2}}}&=\color{#ec0000}{\pm \sqrt{\color{black}{-\dfrac{k}{a}}}}\\
x-h \color{#ec0000}{+h}&=\pm \sqrt{\color{black}{-\dfrac{k}{a}}}\color{#ec0000}{+h}\\
x&=h \pm \sqrt{-\dfrac{k}{a}}\end{align}||
Therefore, the zeroes of a function formula is obtained.
The steps for determining the formula are the same as when using the equation-solving technique. It is why the 2 approaches are equivalent.
-
Replace |f(x)| with |0.|
-
Determine the value of parameters |a,| |h,| and |k.|
-
Apply the zeroes of a function formula.
Determine the zeroes of the function |f(x)=2(x+1)^2-8.|
-
Replace |f(x)| with |0|
||\begin{align}f(x)&=2(x+1)^2-8\\ 0&=2(x+1)^2-8\end{align}|| -
Determine the value of parameters |a,| |h,| and |k|
||a=2,\ h=-1,\ k=-8|| -
Apply the zeroes of a function formula
||\begin{align}x_{1,2}&= h \pm\sqrt{-\dfrac{k}{a}}\\ &= -1 \pm \sqrt{-\dfrac{-8}{2}}\\&= -1 \pm \sqrt{4}\\&= -1 \pm 2\end{align}||
Next, separate the formula into 2 parts, one using |+| and the other using |-.|
||\begin{aligned}x_1&=-1-2\qquad \\&=-3\end{aligned}\begin{aligned}x_2&=-1+2\\&=1\end{aligned}||
Answer: The 2 zeroes of the function are |-3| and |1.|
The number of zeroes in a quadratic function can be determined by analyzing the radicand (the expression under the root) in the zeroes formula.
-
When |- \dfrac{k}{a} >0,| the function has 2 zeroes.
-
When |- \dfrac{k}{a} =0,| the function has 1 zero.
-
When |- \dfrac{k}{a} <0,| the function has no zeroes.
To find the zeroes of a quadratic function in factored form |f(x)=a(x-x_1)(x-x_2),| find the value of |x_1| and |x_2| using the rule. The advantage of this approach is that it results in the value of the zeroes directly.
Find the zeroes of the function |f(x)=-0.5(x+2.7)(x-6.2).|
It is necessary to determine |x_1| and |x_2.| There are subtractions inside the brackets in the rule for factored form, which can be found in this example.
||\begin{align} f(x) &= -0.5(x+2.7)(x-6.2) \\ f(x) &= -0.5\big(x-(\color{#3a9a38}{-2.7})\big)\big(x-\color{#3a9a38}{6.2}\big) \end{align}||
Answer: The 2 zeroes of the function are |-2.7| and |6.2.|
We can apply the same method when the rule is in general form. The following example is identical to the previous one, except it is solved using the zero (or null) product rule.
Find the zeroes of the function |f(x)=-0.5(x+2.7)(x-6.2).|
-
Replace |f(x)| with |0|
||\begin{align}f(x)&=-0.5(x+2.7)(x-6.2) \\ 0&=-0.5(x+2.7)(x-6.2)\end{align}|| -
Factor the polynomial
The polynomial is already factored. -
Apply the zero product rule
Verify the |x| values where the factors are |0.| Since the factor |-0.5| does not contain variable |x,| it is not taken into account.
||\begin{aligned}x+2.7&=0\\ x_1&=-2.7\end{aligned}\qquad\!\! \begin{aligned}x-6.2&=0\\ x_2&=6.2\end{aligned}||
Answer: The zeroes of the function are |-2.7| and |6.2.|