The rule of a sine function is |f(x)=a\sin\!\big(b(x-h)\big)+k.|
Parameter |a| is related to the amplitude.
Parameter |b| is related to the period.
Parameter |h| is related to the phase shift.
Parameter |k| is related to the axis of oscillation.
When looking for the rule of a sinusoidal function (sine function), locate a cycle beginning and ending at an inflection point (i.e., points located on the axis of oscillation). The point at the start of the chosen cycle corresponds to the point |(h,k).|
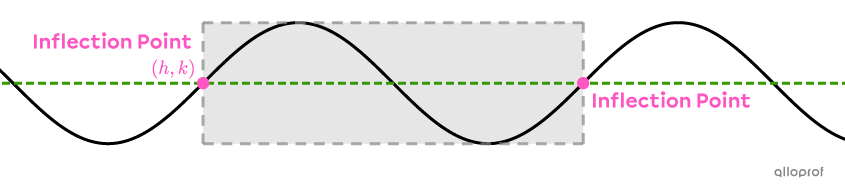
Since there are an infinite number of inflection points for the same sine function, there are an infinite number of possible points |(h,k)|.
-
Determine |h| and |k| using the coordinates of an inflection point.
-
Determine the cycle from the selected point |(h,k)|.
-
Determine |\vert a\vert| from the amplitude.
-
Determine |\vert b\vert| from the period.
-
Determine the signs of |a| and |b.|
If the function is increasing at |(h,k)|, |a| and |b| have the same sign.
If the function is decreasing at |(h,k)|, |a| and |b| have opposite signs. -
Write the rule of the function.
Since the same graph is obtained when |a| and |b| have the same sign, it’s easy to simplify the writing and choose to make them both positive in step 5.
When |a| and |b| have opposite signs, to make writing simpler, it is preferable to assign a positive value to |b| and negative value to |a.| In general, a positive value can always be assigned to |b|, and only the sign of |a| varies.
|a| and |b| have the same sign
||\begin{align}a&>0\\b&>0\end{align}||
|a| and |b| have opposite signs
||\begin{align}a&<0\\b&>0\end{align}||
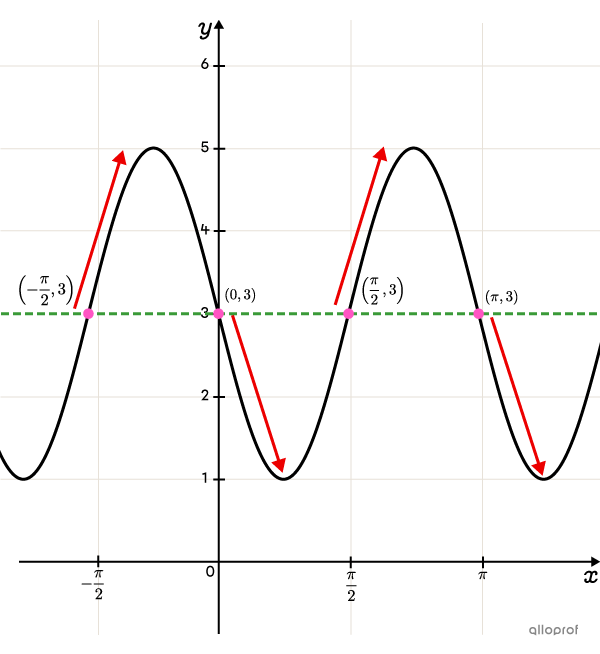
Determine the rule of the sine function represented on the following Cartesian plane.

-
Determine |h| and |k| using the coordinates of an inflection point
According to the graph, the maximum is |5| and the minimum is |1.| Therefore, the axis of oscillation is |\color{#3a9a38}{y=3}.| Note: any of the |4| inflection points could be chosen. We choose the point |\left(-\dfrac{\pi}{2},3\right)\!.|||\begin{align}h&=-\dfrac{\pi}{2}\\k&= 3\end{align}||
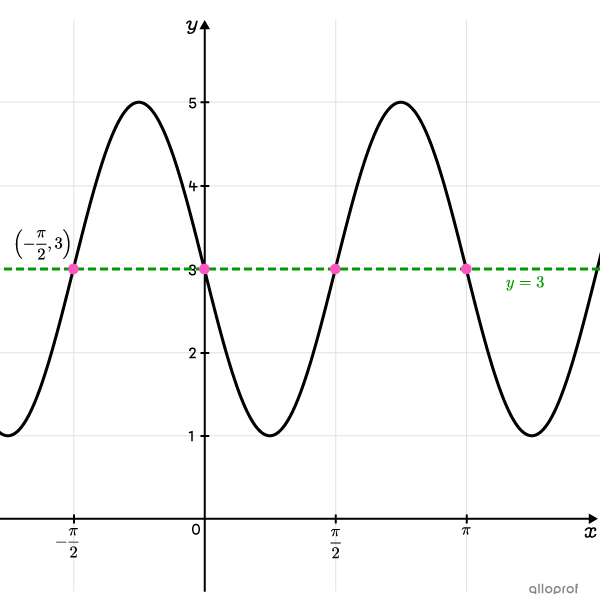
-
Determine the cycle from |(h,k)|
Draw a rectangle around a cycle starting at the point |\left(-\dfrac{\pi}{2},3\right)\!.| The cycle ends at the point |\left(\dfrac{\pi}{2},3\right)\!.| -
Determine |\vert a\vert| from the amplitude
Determine the absolute value of |a| from the amplitude.
||\vert a\vert=\color{#fa7921}A||
According to the graph, the amplitude equals |\color{#fa7921}2| units.
||\vert a\vert=2||
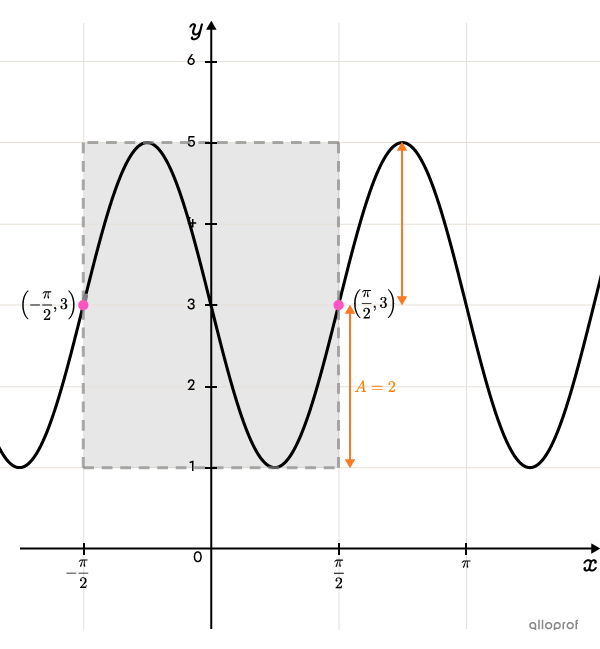
-
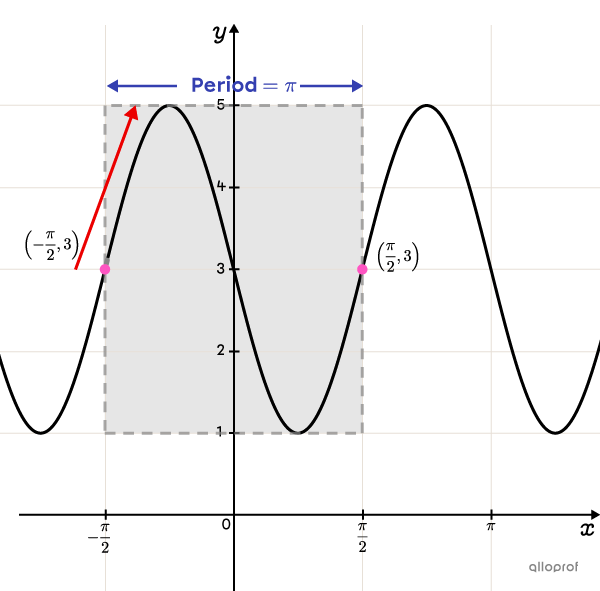
Determine |\vert b\vert| from the period
Determine the absolute value of |b| from the period. According to the graph, the period equals |\color{#333fb1}{\pi}| units.
||\begin{align}\color{#333fb1}p&=\dfrac{2\pi}{\vert b\vert}\\ \color{#333fb1}{\pi}&=\dfrac{2\pi}{\vert b\vert}\ \Leftrightarrow\ \vert b\vert=\dfrac{2\pi}{\pi}\\ &\phantom{\pi=\dfrac{2\pi}{\vert b\vert}\ \Leftrightarrow}\vert b\vert=2\end{align}|| -
Determine the signs of |a| and |b|
Since the function is increasing at |\left(-\dfrac{\pi}{2},3\right)\!,| |a| and |b| have the same sign.
||\begin{aligned}a&>0\\b&>0\end{aligned}
\begin{aligned}\quad \text{or}\quad \end{aligned}
\begin{aligned}a&<0\\b&<0\end{aligned}||
-
Write the function rule
The rule of the sine function is the following.
|f(x)=2\sin\!\bigg(2\left(x+\dfrac{\pi}{2}\right)\!\bigg)+3|
or
|f(x)=-2\sin\!\bigg(-2\left(x+\dfrac{\pi}{2}\right)\!\bigg)+3|
Note: Other answers are possible for the same graph if the point |(h,k)|, chosen in step 1, is different.
When choosing an alternate |(h,k)| point, another rule is used that works just as well for the same graphical representation. However, the variation (increase or decrease) from the chosen inflection point must be taken into account.
In the previous example, choosing the point |\left(-\dfrac{\pi}{2},3\right),| gives the following 2 rules.
|f(x)=2\sin\!\bigg(2\left(x+\frac{\pi}{2}\right)\!\bigg)+3|
or
|f(x)=-2\sin\!\bigg(-2\left(x+\dfrac{\pi}{2}\right)\!\bigg)+3|
If point |(0,3)| was chosen instead, the cycle would have started with a decrease, meaning |a| and |b| would have had opposite signs. In that case, the following 2 rules would have been obtained.
|f(x)=-2\sin\left(2x\right)+3|
or
|f(x)=2\sin\left(-2x\right)+3|
Continuing in the same manner with point |\left(\dfrac{\pi}{2},3\right)| gives the following rules.
|f(x)=2\sin\!\bigg(2\left(x-\dfrac{\pi}{2}\right)\!\bigg)+3|
or
|f(x)=-2\sin\!\bigg(-2\left(x-\dfrac{\pi}{2}\right)\!\bigg)+3|
Analyzing each rule reveals that |\vert a\vert,| |\vert b\vert,| and |k| never change. The only difference between them is the value of |h| and the signs of |a| and |b.|
The following example depicts when the coordinates of the inflection points are not directly provided. More calculations are required to find each parameter.
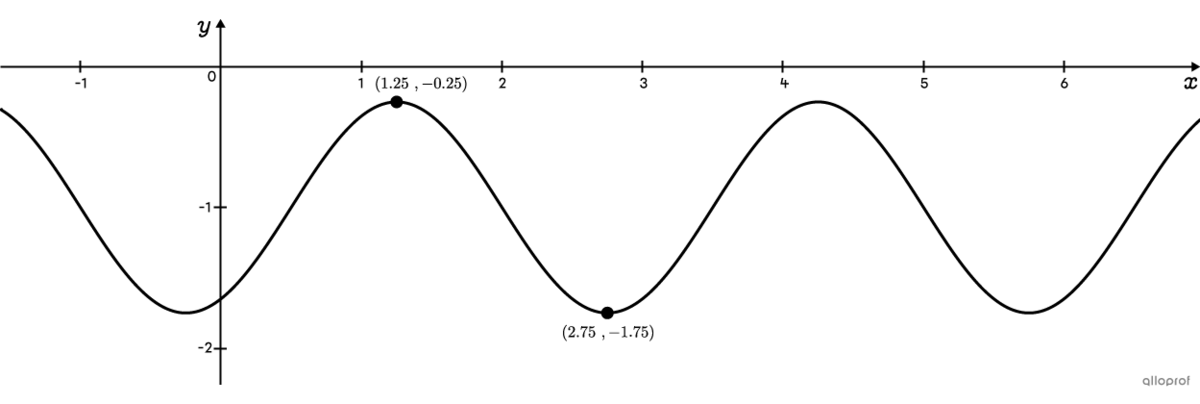
Determine the rule of the sine function passing through points |(1.25,-0.25)| and |(2.75,-1.75),| representing a maximum and a minimum, respectively.
-
Determine |h| and |k| using the coordinates of an inflection point
To determine the value of |h,| analyze the |x|-values of the points provided (|x|-coordinates). For |k,| the |y|-value must be analyzed (|y|-coordinates). Since an inflection point is always located at an equal distance between a minimum and maximum, the coordinates can be found by calculating the average between 2 consecutive extrema.
||\begin{aligned}h&=\dfrac{\max+\min}{2}&k&=\dfrac{\max+\min}{2}\\&=\dfrac{\color{#333fb1}{1.25}+\color{#333fb1}{2.75}}{2}&&=\dfrac{\color{#EC0000}{-0.25}+\color{#EC0000}{-1.75}}{2}\\&=2&&=-1\end{aligned}||

-
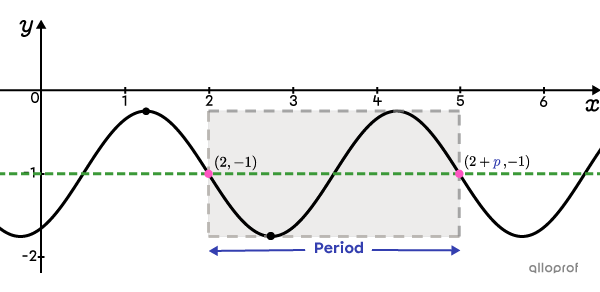
Determine the cycle from |(h,k)|
Draw a rectangle around a cycle starting at the point |(2,-1).| Note that the |y|-coordinate of the point ending the cycle is also |-1.| To find its |x|-coordinate, a period must be added to |h.|
-
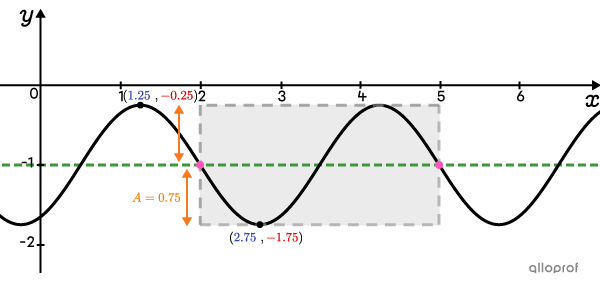
Determine |\vert a\vert| from the amplitude
Determine the absolute value of |a| from the amplitude.
||\begin{align}\vert a\vert&=\color{#fa7921}A\\\vert a\vert&=\dfrac{\max-\min}{2}\\\vert a\vert&=\dfrac{\color{#EC0000}{-0.25}-\color{#EC0000}{-1.75}}{2}\\\vert a\vert&=\color{#fa7921}{0.75}\end{align}||
-
Determine |\vert b\vert| from the period
Determine the absolute value of |b| from the period.
There is a half-period between a maximum and a minimum. To calculate a complete period, proceed as follows.
||\begin{align}\dfrac{1}{2}\color{#333fb1}p&=\color{#333fb1}{2.75} -\color{#333fb1}{1.25}\\\dfrac{1}{2}\color{#333fb1}p&=1.5\\\color{#333fb1}p&=\color{ #333fb1}3\end{align}||
Next, determine |\vert b\vert.| ||\begin{align}\color{#333fb1}p&=\dfrac{2\pi}{\vert b\vert}\\\color{#333fb1}{3}&=\dfrac{2\pi}{\vert b\vert}\ \Leftrightarrow\ \vert b\vert=\dfrac{2\pi}{3}\end{align}|| -
Determine the signs of |a| and |b|
Since the function is decreasing from |(2,-1),| |a| and |b| have opposite signs. ||\begin{aligned}a&>0\\b&<0\end{aligned}\begin{aligned}\quad \text{or}\quad \end{aligned}\begin{aligned}a&<0\\b&>0\end{aligned}|| -
Write the rule of the function
The rule of the sine function is the following.|f(x)=-0.75\sin\left(\dfrac{2\pi}{3}(x-2)\right)-1|
or
|f(x)=0.75\sin\left(-\dfrac{2\pi}{3}(x-2)\right)-1|
When the maximum and minimum of the sinusoidal function are provided, it is best to search for the rule of the cosine function. That way, there are fewer calculations.
When asked to find the equation of a sinusoidal function, it’s possible to use the equation of a sine or a cosine function. The next example shows how the equation of a cosine function can be determined by using the trigonometric identities.
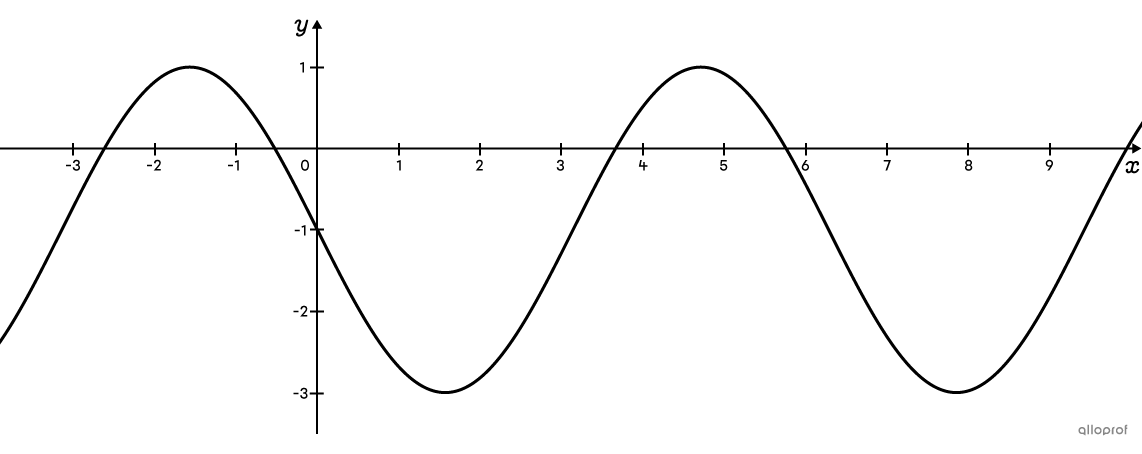
Above is a sinusoidal function where the rule, starting from the sine function, is |f(x)=-2\sin(x)-1.|
To transform the equation into a cosine function, apply the following trigonometric identity: |\sin x=\color{#3A9A38}{\cos}\left(x\color{#3A9A38}{-\dfrac{\pi} {2}}\right).|||\begin{align}f(x)&=-2\sin(x)-1\\f(x)&=-2\color{#3A9A38}{\cos }\left(x\color{#3A9A38}{-\dfrac{\pi}{2}}\right)-1\end{align}||
The 2 previous rules are equivalent.
Note: Although the rule changed from a sine function to a cosine function, |\vert a\vert| and |\vert b\vert| did not change, since the amplitude and the period have remained the same. Notice that |k| did not change either, since the axis of oscillation is also the same.
The only differences between the rules are the value of |h| and the signs of |a| and |b.|
An error was made in this video.
At 6 min 20 s, it should be written |(x+3)| instead of |(x-3).|