A sine equation or inequality contains a sine ratio, where the unknown |(x)| is found in the argument.
Since the sine function is periodic, this type of equation may have no solution, one solution, several solutions, or an infinite number of solutions.
Also, we need to use the angles in radians.
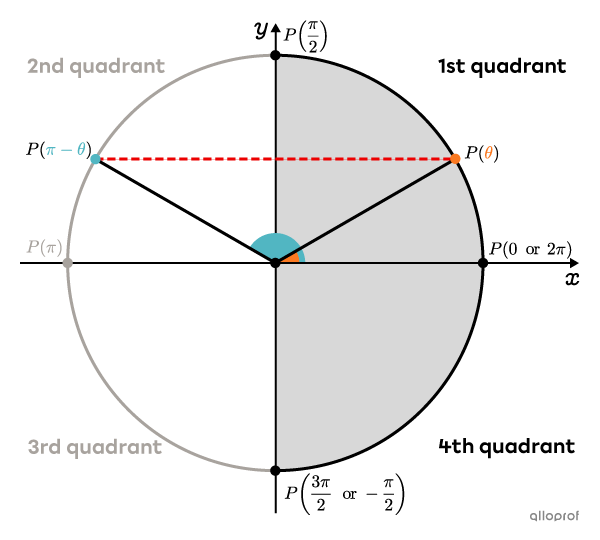
In the unit circle, the sine of an angle corresponds to the y-coordinate of the point on the circle. When solving a sine equation, we look for angles that have a certain y-coordinate. To do so, we can use the main points of the unit circle or the inverse function |\boldsymbol{\arcsin}.|
When we use the unit circle, we generally choose angles located between |0| and |2\pi.|
When using the inverse function |\arcsin,| the result obtained is always an angle in the 1st quadrant or the 4th quadrant of the unit circle. In other words, the angle is between |-\dfrac{\pi}{2}| and |\dfrac{\pi}{2}.|
However, there are always 2 different trigonometric angles with the same y-coordinate. This is why, from the angle obtained |\boldsymbol{\color{#fa7921}{(\theta)}},| we find the 2nd angle by calculating |\boldsymbol{\color{#51b6c2}{\pi-\theta}}.|
The inverse function |\arcsin| is sometimes denoted |\sin^{-1},| especially on calculators.
The procedure for solving a sine equation is as follows:
-
Isolate the sine ratio.
-
Find the trigonometric angles.
- If the sine ratio is equal to the y-coordinate of one of the main points, use the unit circle.
- If not, use the inverse function |\boldsymbol{\arcsin}.| -
Solve the equations obtained with the trigonometric angles.
-
Calculate the period of the sine function.
-
Give the solutions of the equation.
Here's an example using the main points of the unit circle to solve the equation.
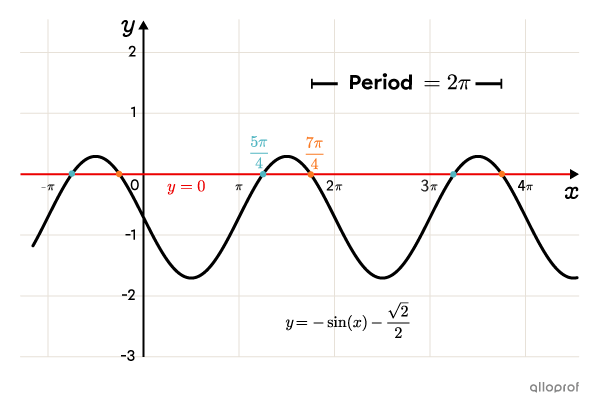
Solve the following equation:||-\sin(x)-\dfrac{\sqrt{2}}{2}=0||
Solve the following equation:||-\sin(x)-\dfrac{\sqrt{2}}{2}=0||
-
Isolate the sine ratio.
||\begin{align}-\sin(x)-\dfrac{\sqrt{2}}{2}&=0\\[3pt]-\sin(x)&=\dfrac{\sqrt{2}}{2}\\[3pt]\sin(x)&=-\dfrac{\sqrt{2}}{2}\end{align}|| -
Determine the trigonometric angles.
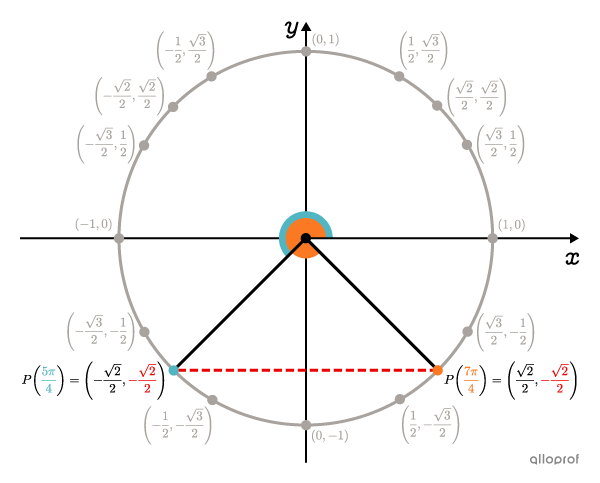
Since |\boldsymbol{\color{#ec0000}{-\dfrac{\sqrt{2}}{2}}}| is a y-coordinate of one of the main points, we can determine the angles sought directly from the unit circle.
We find that the angles with a y-coordinate of |-\dfrac{\sqrt{2}}{2}| are |\boldsymbol{\color{#51b6c2}{\dfrac{5\pi}{4}}}| and |\boldsymbol{\color{#fa7921}{\dfrac{7\pi}{4}}}.|
-
Solve the equations.
We get the following 2 equations that are created using the angles found in the last step.
||\begin{align}\sin(x)&=-\dfrac{\sqrt{2}}{2}\\ &\Downarrow\\\boldsymbol{\color{#51b6c2}{x_1}}&=\boldsymbol{\color{#51b6c2}{\dfrac{5\pi}{4}}}\end{align}||
||\begin{align}\sin(x)&=-\dfrac{\sqrt{2}}{2}\\ &\Downarrow\\\boldsymbol{\color{#fa7921}{x_2}}&=\boldsymbol{\color{#fa7921}{\dfrac{7\pi}{4}}}\end{align}||
-
Calculate the period of the sine function.
The sine function is periodic, so we need to calculate the period in order to determine all the solutions.||\begin{align}p&=\dfrac{2\pi}{\vert b\vert}\\[3pt]&=\dfrac{2\pi}{\vert1\vert}\\[3pt]&=2\pi\end{align}||
-
Give the solutions of the equation.
The solutions of the equation |-\sin(x)-\dfrac{\sqrt{2}}{2}=0| are therefore as follows:
||x=\begin{cases}\dfrac{5\pi}{4}+2\pi n\\[3pt]\dfrac{7\pi}{4}+2\pi n\end{cases}||where||n\in\mathbb{Z}||
Here's an example that uses the inverse function arcsine to solve the equation.
Solve the following equation for the interval |[0,2\pi].|||\sin\!\big(2(x-3)\big)-1=-\dfrac{1}{3}||
-
Isolate the sine ratio.
||\begin{align}\sin\!\big(2(x-3)\big)-1&=-\dfrac{1}{3}\\[3pt]\sin\!\big(2(x-3)\big)&=\dfrac{2}{3}\end{align}|| -
Determine the trigonometric angles.
Since |\boldsymbol{\color{#ec0000}{\dfrac{2}{3}}}| is not a y-coordinate of one of the main points, we determine the 1st angle sought using |\arcsin.|||\begin{align}\sin\!\big(2(x-3)\big)&=\dfrac{2}{3}\\&\Downarrow\\\boldsymbol{\color{#fa7921}{2(x-3)}}&=\arcsin\left(\dfrac{2}{3}\right)\\[3pt]&\approx\boldsymbol{\color{#fa7921}{0.73}}\end{align}||The 2nd angle is found as follows:||\begin{align}\boldsymbol{\color{#51b6c2}{2(x-3)}}&\approx\pi-0.73\\&\approx\boldsymbol{\color{#51b6c2}{2.41}}\end{align}||
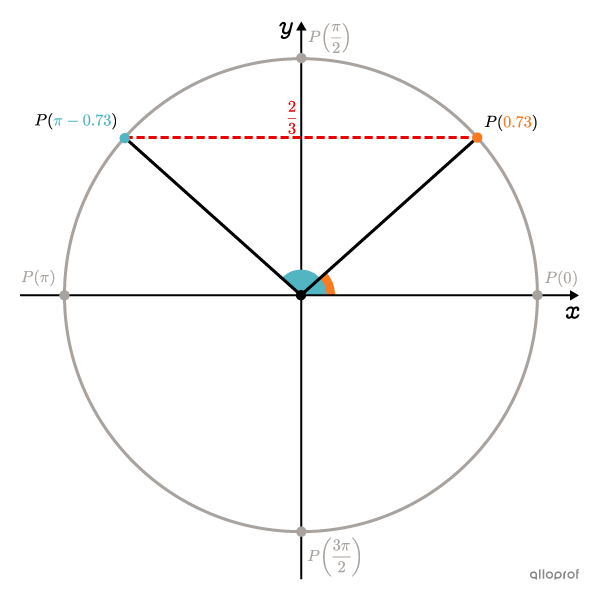
-
Solve the equations.
We get the following 2 equations that are formed from the angles found in the last step, and solve them.
||\begin{align}2(x-3)&\approx0.73\\x-3&\approx0.37\\\boldsymbol{\color{#fa7921}{x_1}}&\approx\boldsymbol{\color{#fa7921}{3.37}}\end{align}||
||\begin{align}2(x-3)&\approx2.41\\x-3&\approx1.21\\\boldsymbol{\color{#51b6c2}{x_2}}&\approx\boldsymbol{\color{#51b6c2}{4.21}}\end{align}||
-
Calculate the period of the sine function.
The sine function is periodic, so we need to calculate the period in order to determine all the solutions.||\begin{align}p&=\dfrac{2\pi}{\vert b\vert}\\[3pt]&=\dfrac{2\pi}{\vert2\vert}\\&=\pi\end{align}||
-
Give the solutions of the equation.
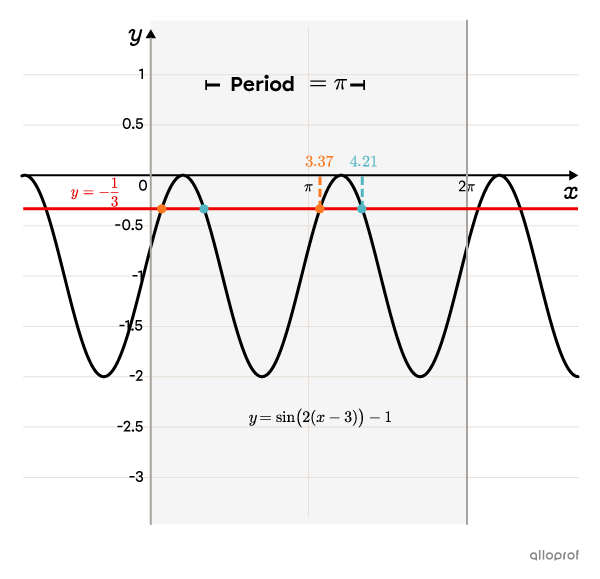
Since we're looking for solutions within the interval |[0,2\pi],| there is a finite number of solutions. The other solutions are calculated by adding or subtracting the period |(\pi)| to the 2 answers found in step 3, without exceeding the interval.
Solutions from |\boldsymbol{x_1}|
We keep |3.37,| since this value is found inside the interval |[0,2\pi].| ||\begin{align}x&\approx 3.37+\pi\\&\approx6.51\end{align}||We reject |6.51,| since this value is larger than |2\pi.| ||\begin{align}x&\approx3.37-\pi\\&\approx0.23\end{align}|| We keep |0.23,| since this value is found inside the interval |[0,2\pi].| ||\begin{align}x&\approx0.23-\pi\\&\approx-2.91\end{align}|| We reject |-2.91,| since this value is less than |0.|
Solutions from |\boldsymbol{x_2}|
We keep |4.21,| since this value is found inside the interval |[0,2\pi].| ||\begin{align}x&\approx 4.21+\pi\\&\approx7.35\end{align}|| We reject |7.35,| since this value is larger than |2\pi.| ||\begin{align}x&\approx4.21-\pi\\&\approx1.07\end{align}|| We keep |1.07,| since this value is found inside the interval |[0,2\pi].| ||\begin{align}x&\approx1.07-\pi\\&\approx-2.07\end{align}|| We reject |-2.07,| since this value is less than |0.|
The solutions of the equation |\sin\!\big(2(x-3)\big)-1=-\dfrac{1}{3}| for the interval |[0,2\pi]| are the following:||x\in\{0.23,\ 1.07,\ 3.37,\ 4.21\}||
Here's an example of solving a 2nd degree sine equation.
Solve the following equation:||2\sin^2\left(\dfrac{x+\pi}{3}\right)-\sin\left(\dfrac{x+\pi}{3}\right)-1=0||
A sine equation of this type can be solved using the same strategies we use to solve a 2nd degree polynomial equation. In other words, you can use factoring or the quadratic formula.
To do so, we need to change the variable by replacing |\sin\left(\dfrac{x+\pi}{3}\right)| with |z.| This way, we can temporarily set aside the sine ratios and concentrate on solving the 2nd degree polynomial.
The result is the following equation:||2\sin^2\left(\dfrac{x+\pi}{3}\right)-\sin\left(\dfrac{x+\pi}{3}\right)-1=0\\\Updownarrow\\2z^2-z-1=0|| Using the quadratic formula, we obtain the following solutions for |z|:||\begin{align}z_{1,2}&=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}\\[3pt]&=\dfrac{-(-1)\pm\sqrt{(-1)^2-4(2)(-1)}}{2(2)}\\[3pt]&=\dfrac{1\pm\sqrt{9}}{4}\\\\z_1&=1\quad\text{and}\quad z_2=-\dfrac{1}{2}\end{align}||The solutions of the equation |2z^2-z-1=0| are therefore |z_1=1| and |z_2=-\dfrac{1}{2}.| Since we changed variables, we can substitute |z| with |\sin\left(\dfrac{x+\pi}{3}\right).| We get the following 2 equations:
||\sin\left(\dfrac{x+\pi}{3}\right)=1||
||\sin\left(\dfrac{x+\pi}{3}\right)=-\dfrac{1}{2}||
We can now proceed as we would for a 1st degree sine equation.
-
Isolate the sine ratio.
The sine ratio is already isolated in both equations.
-
Determine the trigonometric angles.
Since |\boldsymbol{\color{#ec0000}{1}}| and |\boldsymbol{\color{#ec0000}{-\dfrac{1}{2}}}| are y-coordinates of main points, we can find the angles sought directly from the unit circle.
We find that the angle when the y-coordinate is |1| is |\boldsymbol{\color{#ff55c3}{\dfrac{\pi}{2}}},| and that the angles when the y-coordinate is |-\dfrac{1}{2}| are |\boldsymbol{\color{#51b6c2}{\dfrac{7\pi}{6}}}| and |\boldsymbol{\color{#fa7921}{\dfrac{11\pi}{6}}}.|
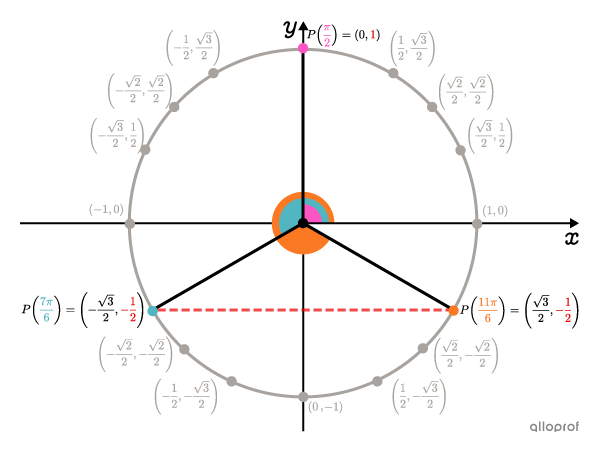
-
Solve the equations.
We get the following 3 equations, which are formed using the angles found in the last step, and solve them.
||\begin{align}\sin\left(\dfrac{x+\pi}{3}\right)&=1\\&\Downarrow\\\dfrac{x+\pi}{3}&=\dfrac{\pi}{2}\\[3pt]x+\pi&=\dfrac{3\pi}{2}\\[3pt]\boldsymbol{\color{#ff55c3}{x_1}}&=\boldsymbol{\color{#ff55c3}{\dfrac{\pi}{2}}}\end{align}||
||\begin{align}\sin\left(\dfrac{x+\pi}{3}\right)&=-\dfrac{1}{2}\\&\Downarrow\\\dfrac{x+\pi}{3}&=\dfrac{7\pi}{6}\\[3pt]x+\pi&=\dfrac{7\pi}{2}\\[3pt]\boldsymbol{\color{#51b6c2}{x_2}}&=\boldsymbol{\color{#51b6c2}{\dfrac{5\pi}{2}}}\end{align}||
||\begin{align}\sin\left(\dfrac{x+\pi}{3}\right)&=-\dfrac{1}{2}\\&\Downarrow\\\dfrac{x+\pi}{3}&=\dfrac{11\pi}{6}\\[3pt]x+\pi&=\dfrac{11\pi}{2}\\[3pt]\boldsymbol{\color{#fa7921}{x_3}}&=\boldsymbol{\color{#fa7921}{\dfrac{9\pi}{2}}}\end{align}||
-
Calculate the period of the sine function.
The sine function is periodic, so the period must be calculated to be able to give all the solutions.||\begin{align}p&=\dfrac{2\pi}{\vert b\vert}\\[3pt]&=\dfrac{2\pi}{\left\vert\frac{1}{3}\right\vert}\\[3pt]&=6\pi\end{align}||
-
Give the solutions of the equation.
The solutions of the equation |2\sin^2\left(\dfrac{x+\pi}{3}\right)-\sin\left(\dfrac{x+\pi}{3}\right)-1=0| are the following:
||x\in\left\{\dfrac{\pi}{2}+6\pi n,\ \dfrac{5\pi}{2}+6\pi n,\ \dfrac{9\pi}{2}+6\pi n\right\}||where||n\in\mathbb{Z}||
We can also write the solutions in the following form.
||x=\dfrac{\pi}{2}+2\pi n||where||n\in\mathbb{Z}||
We can use a technological tool to plot the solutions on the graph of the 2nd degree sine function. Sketching this sort of graph is not part of the high school curriculum.
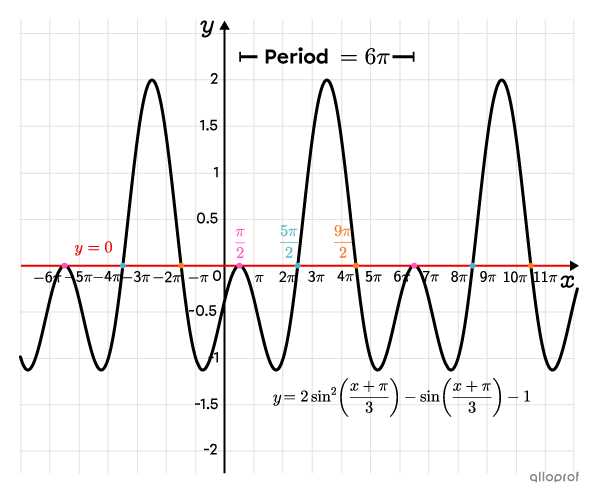
The procedure for solving a sine inequality is as follows:
-
Change the inequality symbol to an equal symbol.
-
Isolate the sine ratio.
-
Determine the trigonometric angles.
- If the sine ratio is equal to a y-coordinate of one of the main points, use the unit circle.
- If not, use the inverse function |\boldsymbol{\arcsin}.| -
Solve the equations obtained with the trigonometric angles.
-
Calculate the period of the sine function.
-
Give the solution set of the inequality.
Here's an example using the main points of the unit circle to solve the inequality.
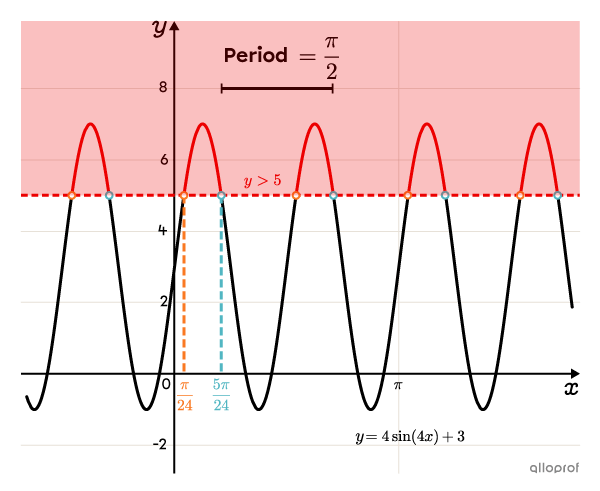
Solve the following inequality:||4\sin(4x)+3>5||
-
Change the inequality symbol to an equal symbol.
||\begin{align}4\sin(4x)+3&>5\\&\downarrow\\4\sin(4x)+3&=5\end{align}|| -
Isolate the sine ratio.
||\begin{align}4\sin(4x)+3&=5\\4\sin(4x)&=2\\[3pt]\sin(4x)&=\dfrac{1}{2}\end{align}|| -
Determine the trigonometric angles.
Since |\boldsymbol{\color{#ec0000}{\dfrac{1}{2}}}| is a y-coordinate of one of the main points, we can determine the angles sought directly from the unit circle.
We find that the angles with a y-coordinate of |\dfrac{1}{2}| are |\boldsymbol{\color{#fa7921}{\dfrac{\pi}{6}}}| and |\boldsymbol{\color{#51b6c2}{\dfrac{5\pi}{6}}}.|
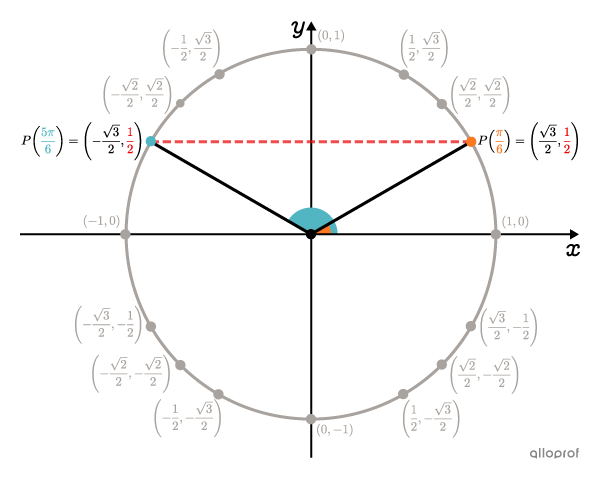
-
Solve the equations.
We get the following equations, formed using the angles found in the last step, and solve them.
||\begin{align}\sin(4x)&=\dfrac{1}{2}\\&\Downarrow\\4x&=\dfrac{\pi}{6}\\[3pt]\boldsymbol{\color{#fa7921}{x_1}}
&=\boldsymbol{\color{#fa7921}{\dfrac{\pi}{24}}}\end{align}||
||\begin{align}\sin(4x)&=\dfrac{1}{2}\\&\Downarrow\\4x&=\dfrac{5\pi}{6}\\[3pt]\boldsymbol{\color{#51b6c2}{x_2}}
&=\boldsymbol{\color{#51b6c2}{\dfrac{5\pi}{24}}}\end{align}||
-
Calculate the period of the sine function.
The sine function is periodic, so the period must be calculated to be able to give all the solutions.||\begin{align}p&=\dfrac{2\pi}{\vert b\vert}\\[3pt]&=\dfrac{2\pi}{\vert4\vert}\\[3pt]&=\dfrac{\pi}{2}\end{align}||
-
Give the solution set of the inequality.
There are 2 possible intervals: either between |\boldsymbol{\color{#fa7921}{x_1}}| and |\boldsymbol{\color{#51b6c2}{x_2}};| and between |\boldsymbol{\color{#51b6c2}{x_2}}| and the following |\boldsymbol{\color{#fa7921}{x}},| located one period farther than |\boldsymbol{\color{#fa7921}{x_1}}.| To determine which interval is part of the solution set, we can use the graph or test an |x| value in each interval.
Note: Since the inequality symbol is |>,| the boundaries of the interval are excluded from the solution set.
||\left]\boldsymbol{\color{#fa7921}{\dfrac{\pi}{24}}},\boldsymbol{\color{#51b6c2}{\dfrac{5\pi}{24}}}\right[||Let’s test |x=\dfrac{3\pi}{24}.| ||\begin{align}4\sin(4x)+3&>5\\[3pt]4\sin\left(4\times\dfrac{3\pi}{24}\right)+3&\overset{\text{?}}{>}5\\[3pt]4\sin\left(\dfrac{\pi}{2}\right)+3&\overset{\text{?}}{>}5\\4\times1+3&\overset{\text{?}}{>}5\\7&>5\end{align}|| This inequality is true, which means that the interval |\left]\boldsymbol{\color{#fa7921}{\dfrac{\pi}{24}}},\boldsymbol{\color{#51b6c2}{\dfrac{5\pi}{24}}}\right[| is part of the solution set.
||\begin{align}\left]\boldsymbol{\color{#51b6c2}{\dfrac{5\pi}{24}}},\boldsymbol{\color{#fa7921}{\dfrac{\pi}{24}}}+p\right[&=
\left]\boldsymbol{\color{#51b6c2}{\dfrac{5\pi}{24}}},\boldsymbol{\color{#fa7921}{\dfrac{\pi}{24}}}+\dfrac{\pi}{2}\right[\\[3pt]&=\left]\boldsymbol{\color{#51b6c2}{\dfrac{5\pi}{24}}},\boldsymbol{\color{#fa7921}{\dfrac{13\pi}{24}}}\right[\end{align}||Let’s test |x=\dfrac{12\pi}{24}.| ||\begin{align}4\sin(4x)+3&>5\\[3pt]4\sin\left(4\times\dfrac{12\pi}{24}\right)+3&\overset{\text{?}}{>}5\\4\sin(2\pi)+3&\overset{\text{?}}{>}5\\4\times0+3&\overset{\text{?}}{>}5\\3&\color{#ec0000}{\not>}5\end{align}|| This inequality is false, which means that the interval |\left]\boldsymbol{\color{#51b6c2}{\dfrac{5\pi}{24}}},\boldsymbol{\color{#fa7921}{\dfrac{13\pi}{24}}}\right[| is not part of the solution set.
Since the boundaries of the interval repeat themselves in every period, the solution set of the inequality |4\sin(4x)+3>5| is as follows:
||x\in\left]\dfrac{\pi}{24}+\dfrac{\pi}{2}n,\ \dfrac{5\pi}{24}+\dfrac{\pi}{2}n\right[|| where ||n\in\mathbb{Z}||
Here's an example of how to use the inverse function arcsine to solve the inequality.
Solve the following inequality:||-10\sin\left(\dfrac{2(x-1)}{3}\right)+4\ge12||
Solve the following inequality:||-10\sin\left(\dfrac{2(x-1)}{3}\right)+4\ge12||
-
Change the inequality symbol to an equal symbol.
||\begin{align}-10\sin\left(\dfrac{2(x-1)}{3}\right)+4&\ge12\\&\downarrow\\-10\sin\left(\dfrac{2(x-1)}{3}\right)+4&=12\end{align}|| -
Isolate the sine ratio.
||\begin{align}-10\sin\left(\dfrac{2(x-1)}{3}\right)+4&=12\\[3pt]-10\sin\left(\dfrac{2(x-1)}{3}\right)&=8\\[3pt]\sin\left(\dfrac{2(x-1)}{3}\right)&=-\dfrac{4}{5}\end{align}|| -
Determine the trigonometric angles.
Since |\boldsymbol{\color{#ec0000}{-\dfrac{4}{5}}}| is not a y-coordinate of one of the main points, we determine the 1st angle sought using |\arcsin.| ||\begin{align}\sin\left(\dfrac{2(x-1)}{3}\right)&=-\dfrac{4}{5}\\&\Downarrow\\\boldsymbol{\color{#fa7921}{\dfrac{2(x-1)}{3}}}&=\arcsin\left(-\dfrac{4}{5}\right)\\[3pt]&\approx\boldsymbol{\color{#fa7921}{-0.93}}\end{align}||The 2nd angle is found as follows:||\begin{align}\boldsymbol{\color{#51b6c2}{\dfrac{2(x-1)}{3}}}&\approx\pi--0.93\\[3pt]&\approx\boldsymbol{\color{#51b6c2}{4.07}}\end{align}||
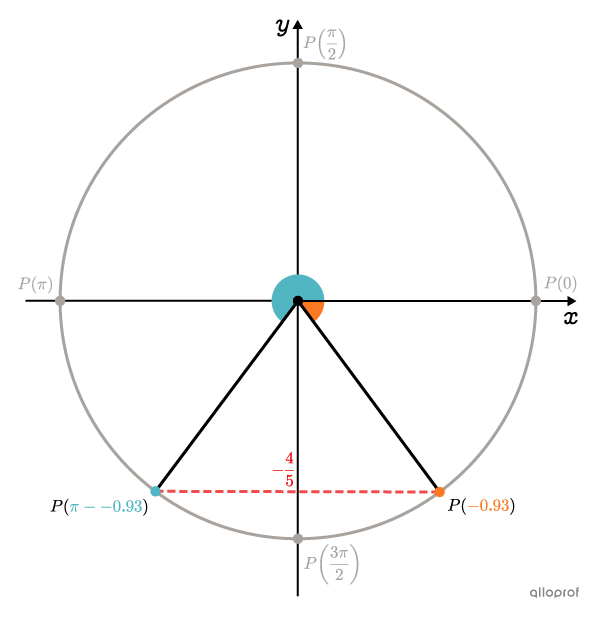
-
Solve the equations.
We get the following equations, formed using the angles found in the last step, and solve them.
||\begin{align}\dfrac{2(x-1)}{3}&\approx-0.93\\[3pt]x-1&\approx-1.4\\\boldsymbol{\color{#fa7921}{x_1}}&\approx\boldsymbol{\color{#fa7921}{-0.4}}\end{align}||
||\begin{align}\dfrac{2(x-1)}{3}&\approx4.07\\[3pt]x-1&\approx6.11\\\boldsymbol{\color{#51b6c2}{x_2}}&\approx\boldsymbol{\color{#51b6c2}{7.11}}\end{align}||
-
Calculate the period of the sine function.
The sine function is periodic, so the period must be calculated to be able to give all the solutions.||\begin{align}p&=\dfrac{2\pi}{\vert b\vert}\\[3pt]&=\dfrac{2\pi}{\left\vert\frac{2}{3}\right\vert}\\[3pt]&=3\pi\end{align}||
-
Give the solution set of the inequality.
There are 2 possible intervals: either between |\boldsymbol{\color{#fa7921}{x_1}}| and |\boldsymbol{\color{#51b6c2}{x_2}};| and between |\boldsymbol{\color{#51b6c2}{x_2}}| and the following |\boldsymbol{\color{#fa7921}{x}},| located one period farther than |\boldsymbol{\color{#fa7921}{x_1}}.| To determine which interval is part of the solution set, we can use the graph or test an |x| value in each interval.
Note: Since the inequality symbol is |\ge,| the boundaries of the interval are included in the solution set.
||\left[\boldsymbol{\color{#fa7921}{-0.4}},\ \boldsymbol{\color{#51b6c2}{7.11}}\right]|| Let’s test |x=0.| ||\begin{align}-10\sin\left(\dfrac{2(x-1)}{3}\right)+4&\ge12\\[3pt]-10\sin\left(\dfrac{2(0-1)}{3}\right)+4&\overset{\text{?}}{\ge}12\\[3pt]-10\sin\left(-\dfrac{2}{3}\right)+4&\overset{\text{?}}{\ge}12\\[3pt]10.18&\color{#ec0000}{\not\ge}12\end{align}|| This inequality is false, which means that the interval |\left[\boldsymbol{\color{#fa7921}{-0.4}},\boldsymbol{\color{#51b6c2}{7.11}}\right]| is not part of the solution set.
||\begin{align}\left[\boldsymbol{\color{#51b6c2}{7.11}},\,\boldsymbol{\color{#fa7921}{-0.4}}+p\right]&= \left[\boldsymbol{\color{#51b6c2}{7.11}},\,\boldsymbol{\color{#fa7921}{-0.4}}+3\pi\right]\\&=\left[\boldsymbol{\color{#51b6c2}{7.11}},\ \boldsymbol{\color{#fa7921}{9.02}}\right]\end{align}|| Let’s test |x=8.| ||\begin{align}-10\sin\left(\dfrac{2(x-1)}{3}\right)+4&\ge12\\[3pt]-10\sin\left(\dfrac{2(8-1)}{3}\right)+4&\overset{\text{?}}{\ge}12\\[3pt]-10\sin\left(\dfrac{14}{3}\right)+4&\overset{\text{?}}{\ge}12\\[3pt]13.99&\ge12\end{align}|| This inequality is true, which means that the interval |\left[\boldsymbol{\color{#51b6c2}{7.11}},\ \boldsymbol{\color{#fa7921}{9.02}}\right]| is part of the solution set.
Since the boundaries of the interval repeat themselves in every period, the solution set of the inequality |-10\sin\left(\dfrac{2(x-1)}{3}\right)+4\ge12| is as follows:
||x\in[7.11+3\pi n,\ 9.02+3\pi n]|| where ||n\in\mathbb{Z}||
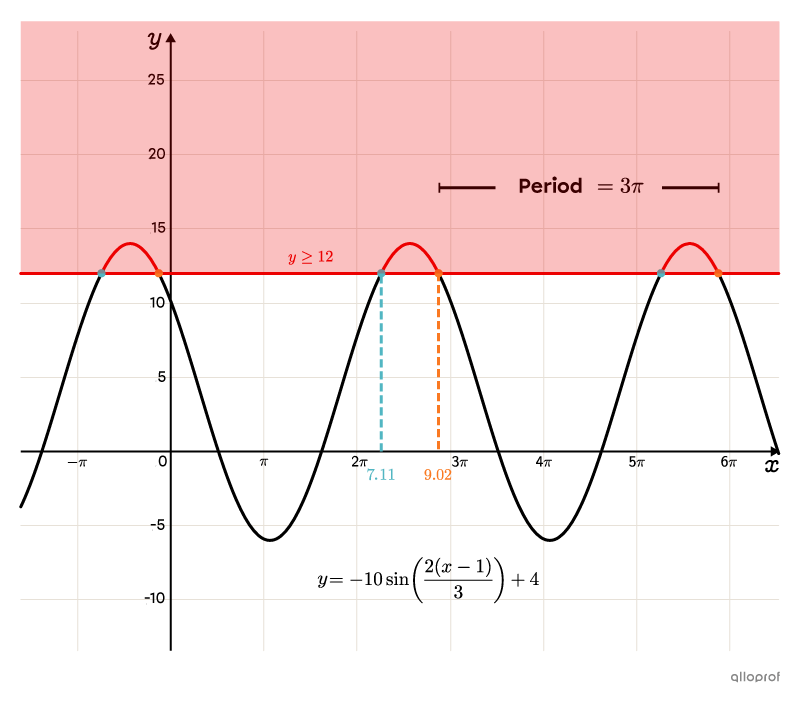
Here's an example of solving a 2nd degree sine inequality.
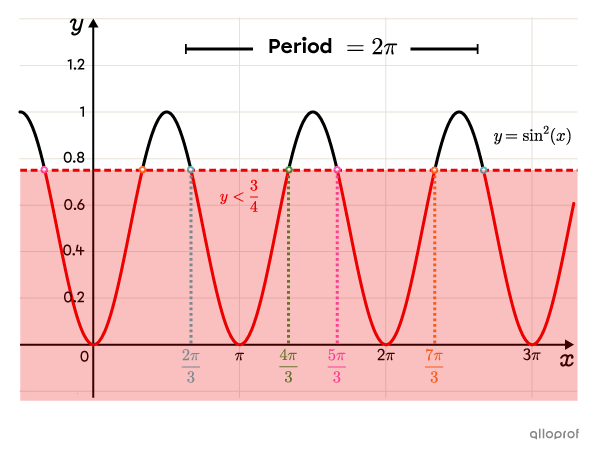
Solve the following inequality:||\sin^2(x)<\dfrac{3}{4}||
-
Change the inequality symbol to an equal symbol.
||\begin{align}\sin^2(x)&<\dfrac{3}{4}\\&\downarrow\\\sin^2(x)&=\dfrac{3}{4}\end{align}|| -
Isolate the sine ratio.
||\begin{align}\sin^2(x)&=\dfrac{3}{4}\\[3pt]\sin(x)&=\pm\sqrt{\dfrac{3}{4}}\\[3pt]\sin(x)&=\pm\dfrac{\sqrt{3}}{2}\end{align}|| -
Determine the trigonometric angles.
Since |\boldsymbol{\color{#ec0000}{\dfrac{\sqrt{3}}{2}}}| and |\boldsymbol{\color{#ec0000}{-\dfrac{\sqrt{3}}{2}}}| are y-coordinates of main points, we can find the angles sought directly from the unit circle.
We find that the angles when the y-coordinate is |\dfrac{\sqrt{3}}{2}| are |\boldsymbol{\color{#fa7921}{\dfrac{\pi}{3}}}| and |\boldsymbol{\color{#51b6c2}{\dfrac{2\pi}{3}}},| and the angles when the y-coordinate is |-\dfrac{\sqrt{3}}{2}| are |\boldsymbol{\color{#3a9a38}{\dfrac{4\pi}{3}}}| and |\boldsymbol{\color{#ff55c3}{\dfrac{5\pi}{3}}}.|
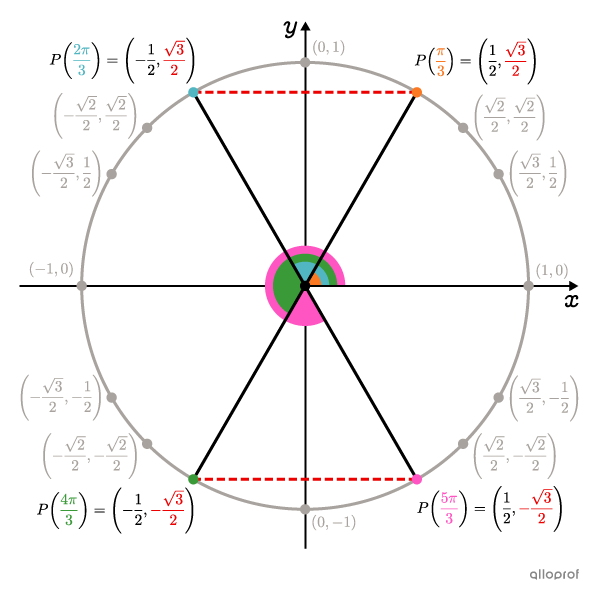
-
Solve the equations.
We get the following equations, formed using the angles found in the last step, and solve them.
||\begin{align}\sin(x)&=\dfrac{\sqrt{3}}{2}\\&\Downarrow\\\boldsymbol{\color{#fa7921}{x_1}}&=\boldsymbol{\color{#fa7921}{\dfrac{\pi}{3}}}\end{align}||
||\begin{align}\sin(x)&=\dfrac{\sqrt{3}}{2}\\&\Downarrow\\\boldsymbol{\color{#51b6c2}{x_2}}&=\boldsymbol{\color{#51b6c2}{\dfrac{2\pi}{3}}}\end{align}||
||\begin{align}\sin(x)&=-\dfrac{\sqrt{3}}{2}\\&\Downarrow\\\boldsymbol{\color{#3a9a38}{x_3}}&=\boldsymbol{\color{#3a9a38}{\dfrac{4\pi}{3}}}\end{align}||
||\begin{align}\sin(x)&=-\dfrac{\sqrt{3}}{2}\\&\Downarrow\\\boldsymbol{\color{#ff55c3}{x_4}}&=\boldsymbol{\color{#ff55c3}{\dfrac{5\pi}{3}}}\end{align}||
-
Calculate the period of the sine function.
The sine function is periodic, so the period must be calculated to be able to give all the solutions.||\begin{align}p&=\dfrac{2\pi}{\vert b\vert}\\[3pt]&=\dfrac{2\pi}{\vert1\vert}\\[3pt]&=2\pi\end{align}||
-
Give the solution set of the inequality.
There are 4 possible intervals: between |\boldsymbol{\color{#fa7921}{x_1}}| and |\boldsymbol{\color{#51b6c2}{x_2}};| between |\boldsymbol{\color{#51b6c2}{x_2}}| and |\boldsymbol{\color{#3a9a38}{x_3}};| between |\boldsymbol{\color{#3a9a38}{x_3}}| and |\boldsymbol{\color{#ff55c3}{x_4}};| and between |\boldsymbol{\color{#ff55c3}{x_4}}| and the following |\boldsymbol{\color{#fa7921}{x}},| located one period farther than |\boldsymbol{\color{#fa7921}{x_1}}.| To determine which interval is part of the solution set, we can use the graph or test an |x| value in each interval.
Note: Since the inequality symbol is |<,| the boundaries of the interval are excluded from the solution set.
||\left]\boldsymbol{\color{#fa7921}{\dfrac{\pi}{3}},\color{#51b6c2}{\dfrac{2\pi}{3}}}\right[|| Let’s test |x=\dfrac{\pi}{2}.| ||\begin{align}\sin^2(x)&<\dfrac{3}{4}\\[3pt]\sin^2\left(\dfrac{\pi}{2}\right)&\overset{\text{?}}{<}\dfrac{3}{4}\\[3pt](1)^2&\overset{\text{?}}{<}\dfrac{3}{4}\\[3pt]1&\color{#ec0000}{\not<}\dfrac{3}{4}\end{align}|| This inequality is false, which means that the interval |\left]\boldsymbol{\color{#fa7921}{\dfrac{\pi}{3}},\color{#51b6c2}{\dfrac{2\pi}{3}}}\right[| is not part of the solution set.
||\left]\boldsymbol{\color{#fa7921}{\dfrac{\pi}{3}},\color{#51b6c2}{\dfrac{2\pi}{3}}}\right[|| Let’s test |x=\pi.| ||\begin{align}\sin^2(x)&<\dfrac{3}{4}\\[3pt]\sin^2(\pi)&\overset{\text{?}}{<}\dfrac{3}{4}\\[3pt](0)^2&\overset{\text{?}}{<}\dfrac{3}{4}\\[3pt]0&<\dfrac{3}{4}\end{align}|| This inequality is true, which means that the interval |\left]\boldsymbol{\color{#51b6c2}{\dfrac{2\pi}{3}},\color{#3a9a38}{\dfrac{4\pi}{3}}}\right[| is part of the solution set.
||\left]\boldsymbol{\color{#3a9a38}{\dfrac{4\pi}{3}},\color{#ff55c3}{\dfrac{5\pi}{3}}}\right[|| Let’s test |x=\dfrac{3\pi}{2}.| ||\begin{align}\sin^2(x)&<\dfrac{3}{4}\\[3pt]\sin^2\left(\dfrac{3\pi}{2}\right)&\overset{\text{?}}{<}\dfrac{3}{4}\\[3pt](-1)^2&\overset{\text{?}}{<}\dfrac{3}{4}\\[3pt]1&\color{#ec0000}{\not<}\dfrac{3}{4}\end{align}|| This inequality is false, which means that the interval |\left]\boldsymbol{\color{#3a9a38}{\dfrac{4\pi}{3}},\color{#ff55c3}{\dfrac{5\pi}{3}}}\right[| is not part of the solution set.
||\begin{align}\left]\boldsymbol{\color{#ff55c3}{\dfrac{5\pi}{3}},\color{#fa7921}{\dfrac{\pi}{3}}}+p\right[&=\left]\boldsymbol{\color{#ff55c3}{\dfrac{5\pi}{3}},{\color{#fa7921}{\dfrac{\pi}{3}}}}+2\pi\right[\\[3pt]&=\left]\boldsymbol{\color{#ff55c3}{\dfrac{5\pi}{3}},{\color{#fa7921}{\dfrac{7\pi}{3}}}}\right[\end{align}|| Let’s test |x=2\pi.| ||\begin{align}\sin^2(x)&<\dfrac{3}{4}\\[3pt]\sin^2(2\pi)&\overset{\text{?}}{<}\dfrac{3}{4}\\[3pt](0)^2&\overset{\text{?}}{<}\dfrac{3}{4}\\[3pt]0&<\dfrac{3}{4}\end{align}|| This inequality is true, which means that the interval |\left]\boldsymbol{\color{#ff55c3}{\dfrac{5\pi}{3}},{\color{#fa7921}{\dfrac{7\pi}{3}}}}\right[| is part of the solution set.
Since the boundaries of the interval repeat themselves in every period, the solution set of the inequality |\sin^2(x)<\dfrac{3}{4}| is as follows:
||x\in\left]\dfrac{2\pi}{3}+2\pi n,\ \dfrac{4\pi}{3}+2\pi n\right[\ \cup\ \left]\dfrac{5\pi}{3}+2\pi n,\ \dfrac{7\pi}{3}+2\pi n\right[|| where ||n\in\mathbb{Z}||
We can also write the solution set as follows:
||x\in\left]\dfrac{2\pi}{3}+\pi n,\ \dfrac{4\pi}{3}+\pi n\right[|| where ||n\in\mathbb{Z}||
We can use a technology tool to graph the 2nd degree sine function. Drawing such a graph is not part of the high school curriculum.