A sine function is a periodic function defined by the |y|-coordinates of the points on the unit circle in relation to the measure of the circle’s angles (in radians).
Some terms need to be defined when working with the sine function. In addition, other related concepts can be reviewed.
The rule of the basic sine function is |f(x)= \sin x.|
The following example demonstrates the relationship between the unit circle and the basic sine function. Each value of |\color{#333FB1}\theta| (in radians) is associated with a point on the circle. Inspecting the |\color{#3A9A38}y|-coordinate of the points, it is possible to sketch the graph.
In the example, move the cursor or the point on the curve to study the connection between them.
-
The basic sine function always passes through the origin.
-
Since the the circle can be rotated an infinite number of times, the domain of the function corresponds to the |\mathbb{R}| set.
-
The sine function has a zero when the angle |\theta| makes half a rotation. Since the circle can be rotated an infinite number of times, the function has an infinite number of zeroes.
||\theta \in\{\dots,\pi,\, 2\pi,\, 3\pi, \dots\}|| -
The maximum value is |1| and the minimum value is |-1,| because the radius of the unit circle is |1| unit.
Analyzing the next example, we notice that the basic cosine function is obtained by a horizontal displacement of |\dfrac{\pi}{2}| units of the basic sine function. In other words, move the |\cos x| function |\dfrac{\pi}{2}| units to the right to obtain the |\sin x| function.
Therefore, we determine the following equality.
||\begin{align}\sin x&=\cos\left(x-\color{#C58AE1}h\right)\\\sin x&=\cos\left(x-\color{#C58AE1}{\dfrac{\pi}{2}}\right)\end{align}||
The same equality is used when working with trigonometric identities.
In the example, move the cursor to observe the phase shift between the sine and cosine functions.
The rule of the transformed sine function is |f(x)=a \sin\big(b(x-h)\big)+k.|
Parameter |a| is related to the amplitude.
Parameter |b| is related to the period.
Parameter |h| is related to the phase shift.
Parameter |k| is related to the axis of oscillation.
The axis of oscillation (also called the midline) corresponds to the horizontal line intersecting the middle of the function.
The axis of oscillation of a sine function is determined by parameter |k.|
||\color{#3a9a38}{\text{Axis of oscillation}}: \color{#3a9a38}{y=k}||
The axis of oscillation can also be found using the extrema.
||k=\dfrac{\max+\min}{2}||

The axis of oscillation is needed to properly define the amplitude of a sine function.
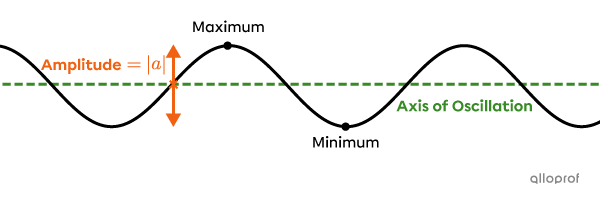
The amplitude |\color{#fa7921}{(A)}| of a sine function is the vertical distance between the axis of oscillation and the maximum or minimum.
The amplitude is determined using parameter |a.|
||\color{#fa7921}{A=\vert a\vert}||
The amplitude can also be found using the extrema.
||\color{#fa7921}A=\dfrac{\max-\min}{2}||
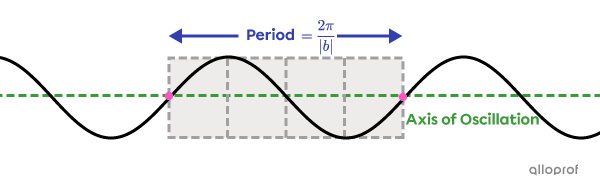
To define the period, identify a cycle. In the sine function, we generally choose a cycle which begins and ends on points located on the axis of oscillation. It helps to graph the sine function and find its rule.
The period |\color{#333fb1}{(p)}| corresponds to the difference between the |x|-values at both ends of a cycle.
The period is determined using parameter |b.|
||\color{#333fb1}{p=\dfrac{2\pi}{\vert b\vert}}||
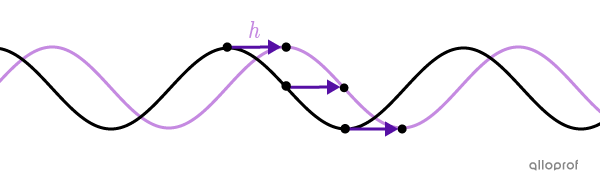
The phase shift corresponds to the horizontal displacement of the transformed sine function relative to the basic function.
The phase shift of a sine function can be determined using parameter |h.|
||\color{#C58AE1}{\text{Phase shift}=h}||
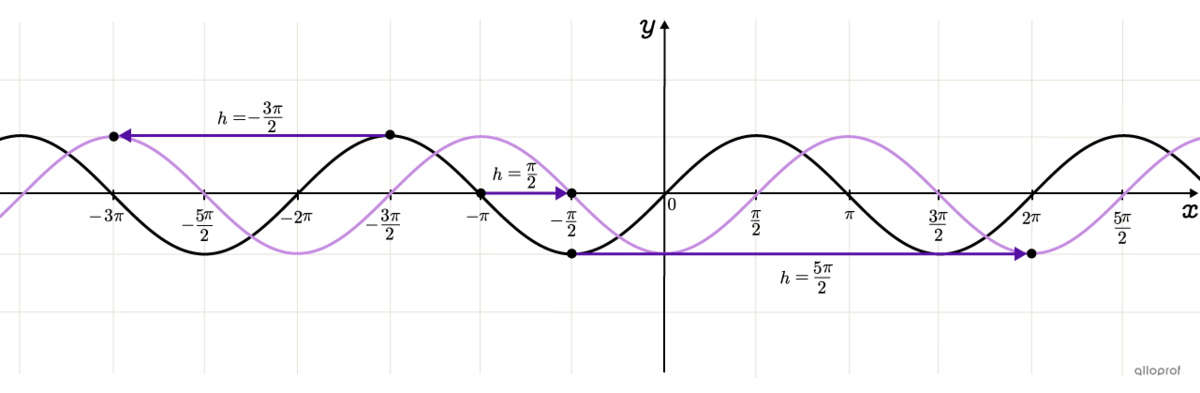
The sine function is periodic, so several possible phase shifts are possible for the same transformed function.
The basic sine function is graphed in black in the image below. The transformed sine function in purple may have undergone a phase shift of |\dfrac{\pi}{2},| or a displacement of |\dfrac{\pi}{2}| units to the right relative to the base function.
It could also have undergone a phase shift of |-\dfrac{3\pi}{2}| units or a displacement of |\dfrac{3\pi}{2}| units to the left, or even |\dfrac{5\pi}{2}| units to the right. These options, and more, are possible and yield the same transformed sine function.