When studying probability, we often do so in the context of a draw with or without replacement from a deck of cards, rolling a die, etc. It is also possible to study probability using different ratios in geometry. This is called geometric probability.
Geometric probability involves a ratio of lengths, areas or volumes between a part of a geometric figure and the whole figure.
To calculate geometric probability, the formulas for perimeter, area and volume are needed.
Note: In all the examples on this page, the probability of hitting a particular place on the figure is considered to be equal to the probability of hitting any other location on the same figure.
When we want to calculate the probability that a portion of a 1-dimensional object (a line, perimeter, etc.) will be affected or selected, we use a ratio of lengths. The probability of Event |(A)| is calculated in the following way:
|P(A)=\dfrac{\text{Length that is hit or chosen}}{\text{Total length}}|
A soccer player chooses a spot on one edge of the field at random. He then kicks a ball straight across the other side of the field as shown below. The ball remains at ground level at all times.
What is the probability of scoring the goal?
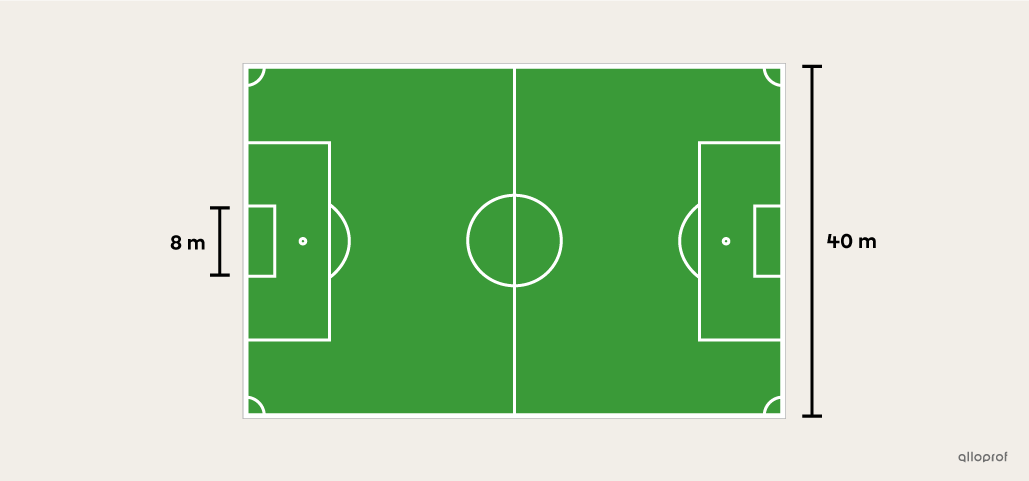
||\begin{align}P(\text{Goal})&=\dfrac{\text{Length to Hit}}{\text{Total Length}}\\&=\dfrac{8\ \text{m}}{40\ \text{m}}\\&=0.2\end{align}||
Answer: The probability of scoring the goal is |0.2,| or |20\ \%.|
A motorist wants to park his car on a street that has 2 fire hydrants situated as shown in the diagram below. He wants to park his car on the same side of the street as the hydrants, but he knows that it is illegal to park within 5 metres of either one of them. If the driver randomly chooses a spot, what is the probability that the front end of his car will be on a part of the street where parking is prohibited?
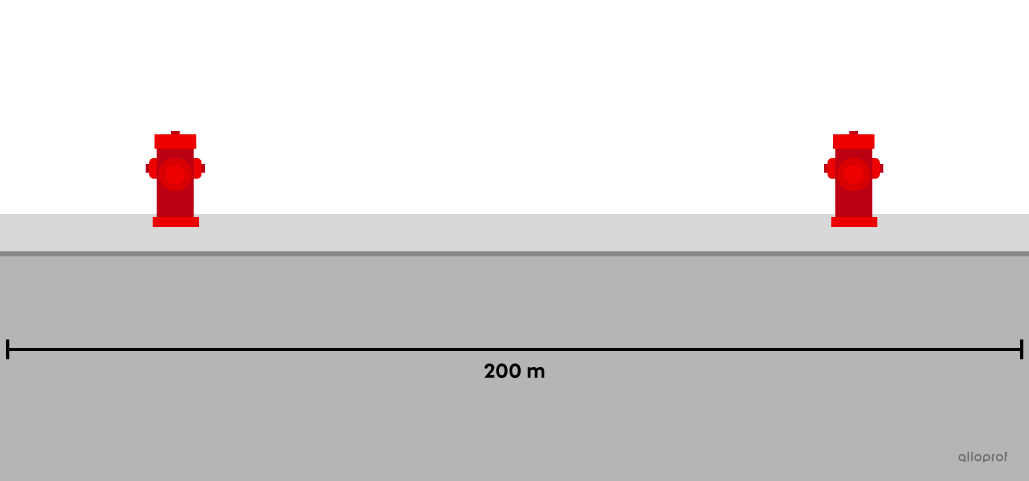
We know that the total distance (the length of the road) is |200\ \text{m}.| It is prohibited to park within |5\ \text{m}| of each fire hydrant. This means that there is a prohibited length of |10\ \text{m}| per hydrant, so |20\ \text{m}| in total.
||\begin{align}P(\text{Prohibited Zone})&=\dfrac{\text{Prohibited Distance}}{\text{Total Distance}}\\&=\dfrac{20\ \text{m}}{200\ \text{m}}\\&=0.1\end{align}||
Answer: The probability that the front end of his car will be parked on a prohibited part of the street is |0.1,| or |10\ \%.|
It is also possible to calculate probability using a ratio of perimeters.
Identically shaped pieces that form the outline of 2 puzzles were mixed together. When completed, the first puzzle has the following dimensions: |50\ \text{cm}| length by |30\ \text{cm}| width. The 2nd puzzle measures |70\ \text{cm}| by |60\ \text{cm}.| What is the probability that a piece chosen at random will belong to the 1st puzzle?
|P(\text{piece is from}\ 1^{\text{st}}\ \text{puzzle})=\dfrac{\text{P}_{1^{\text{st}}\ \text{puzzle}}}{\text{P}_{\text{Total of both puzzles}}}|
The perimeter of the 1st puzzle is calculated as follows:
||\begin{align}\text{P}&=2\times 50+ 2\times 30\\&= 160\ \text{cm}\end{align}||
We can find the perimeter of the 2nd puzzle as follows:
||\begin{align}\text{P}&=2\times 70+ 2\times 60\\&= 260\ \text{cm}\end{align}||
Now we can find the probability that a randomly chosen piece belongs to the 1st puzzle.
||\begin{align}P(\text{Piece is from}\ 1^{\text{st}}\ \text{puzzle})&=\dfrac{\text{P}_{1^{\text{st}}\ \text{puzzle}}}{\text{P}_{\text{Total of both puzzles}}}\\&=\dfrac{160\ \text{cm}}{160\ \text{cm}+260\ \text{cm}}\\&=\dfrac{160\ \text{cm}}{420\ \text{cm}}\\&=\dfrac{8}{21}\end{align}||
Answer: The probability that the randomly selected piece belongs to the 1st puzzle is |\dfrac{8}{21},| or approximately |38\ \%.|
When we want to calculate the probability of a part of a 2-dimensional object being affected or selected, we can use the ratio of areas. The probability of event |A| is calculated as follows:
|P(A)=\dfrac{\text{Area that is hit or chosen}}{\text{Total Area}}|
A dart is thrown at the following square. What is the probability of hitting the circle?

First, we need to calculate the area of the square.
||\begin{align}A_{\text{square}}&=s^2\\&=5^2\\&=25\ \text{cm}^2\end{align}||
Next, we calculate the area of the circle.
||\begin{align}A_{\text{circle}}&=\pi r^2\\&=\pi \left(\dfrac{5}{2}\right)^2\\&\approx19.63\ \text{cm}^2\end{align}||
We can finally calculate the probability of hitting the circle with the dart.
||\begin{align}P(\text{circle})&=\dfrac{A_{\text{circle}}}{A_{\text{square}}}\\&=\dfrac{19.63\ \text{cm}^2}{25\ \text{cm}^2}\\&\approx 0.79\end{align}||
Answer: The probability of hitting the circle is approximately |0.79,| or |79\ \%.|
A dart is thrown at the following figure.

What is the probability of hitting a blue or yellow section?
First, we calculate the total area of the figure, which is a rectangle.
||\begin{align}A_{\text{total}}&=b\times h\\&=15 \times 6\\&= 90\ \text{cm}^2\end{align}||
Next, we calculate the area of the yellow and blue sections.
Area of the yellow sections
||\begin{align}A_{\text{yellow}}&=5 \times (6-4)+8 \times 4\\&= 5\times2+8\times4\\&=10+32\\&=42\ \text{cm}^2\end{align}||
Area of the blue sections
||\begin{align}A_{\text{blue}}&=8 \times (6-4)+(15-8-5) \times 4\\&= 8\times2+2\times4\\&=16+8\\&=24\ \text{cm}^2\end{align}||
We can now calculate the desired probability. Since we are looking for the probability of hitting a blue or a yellow section, we have to add these 2 probabilities.
||\begin{align}P(\text{yellow or blue})&=\dfrac{A_{\text{yellow}}+A_{\text{blue}}}{A_\text{total}}\\&=\dfrac{42+24}{90}\\&=\dfrac{66}{90}\\&=\dfrac{11}{15}\end{align}||
Answer: The probability of hitting a yellow or blue section is |\dfrac{11}{15},| or approximately |73\ \%.|
To calculate the probability that a part of a 3-dimensional object will be affected or selected, we can use a ratio of volumes. The probability of event |A| is calculated as follows:
|P(A)=\dfrac{\text{Volume that is hit or chosen}}{\text{Total volume}}|
A cherry is placed at the bottom of a pitcher that contains |1\ \text{L}| of orange juice. A person pours a cylindrical glass of juice filled to the brim. The glass is |10\ \text{cm}| high and its radius is |3\ \text{cm}.| What is the probability that the cherry will be in the person's glass of juice?

||P(\text{cherry})=\dfrac{V_\text{glass}}{V_\text{total pitcher}}||
It is important to note that a capacity of |1\ \text{L}| equals |1\ \text{dm}^3.| The volume of juice in the pitcher is therefore equal to |1\ \text{dm}^3,| or |1\ 000\ \text{cm}^3.|
We calculate the volume of glass.
||\begin{align}V_{\text{glass}}&=\pi r^2\times h\\&=\pi(3)^2\times 10\\&=90\pi\\&\approx282.74\ \text{cm}^3\end{align}||
Next, we calculate the probability.
||\begin{align}P(\text{cherry})&=\dfrac{V_{\text{glass}}}{V_\text{total of pitcher}}\\&=\dfrac{282.74\ \text{cm}^3}{1\ 000\ \text{cm}^3}\\&\approx 0.28\end{align}||
Answer: The probability that the glass of juice contains the cherry is about |28\ \%.|
When we want to calculate the probability that a part of an object will be affected or selected and we know at least one angle, we can use the ratios of angle measurements. The probability of event |A| is calculated as follows:
|P(A)= \dfrac{\text{Angle bounding the chosen part}}{\text{Angle bounding the entire object}}|
We are making a pizza. There is only one olive left, but we decide to put it on the pizza anyway. Once the meal is done, we cut 2 slices, each bounded by a central angle of |60^\circ.|
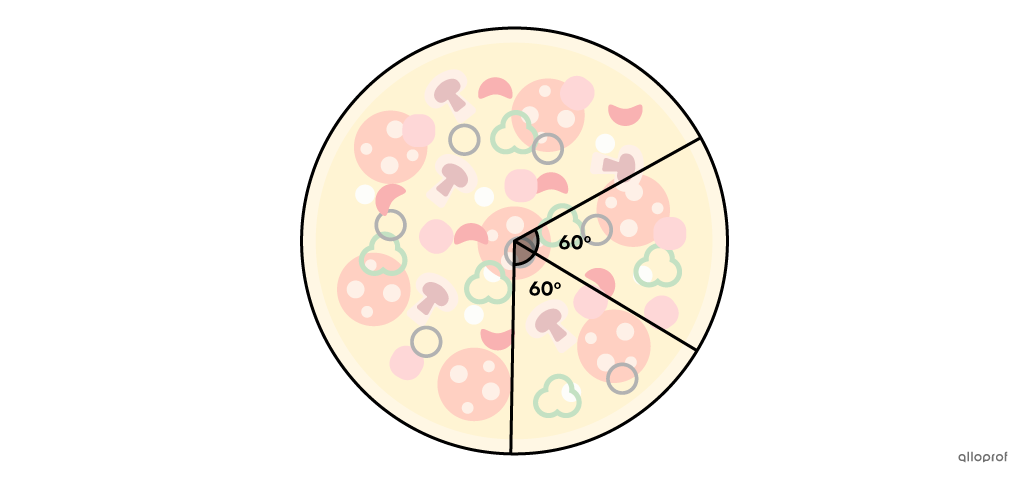
What is the probability that the olive is on one of the 2 slices?
The angle formed by the whole pizza is |360^\circ,| since it forms a complete circle. When the 1st slice is cut, it is cut with a central angle of |60^\circ.| The 2nd slice is also cut at |60^\circ.| So the slices we cut are bounded by a total angle of |120^\circ.|
||\begin{align}P(\text{Olive})&=\dfrac{\text{Total angle of both slices}}{\text{Angle formed by the whole pizza}}\\&=\dfrac{120^\circ}{360^\circ}\\&=\dfrac{1}{3}\end{align}||
Answer: The probability that the olive is on one of the two slices is |\dfrac{1}{3},| or approximately |33\ \%.|
When you want to calculate a probability using data from a Cartesian plane, you have to be careful when you read the question. Sometimes it involves a ratio of lengths or a ratio of areas.
In a Cartesian plane, we notice a segment that starts at the point |(0,6)| and ends at the point |(10,0).| This segment passes through the centre of a circle located at the point |(5,3).| The point |(7,4)| is a point on the circle. We randomly choose a point on the line. What is the probability that it is inside the circle?
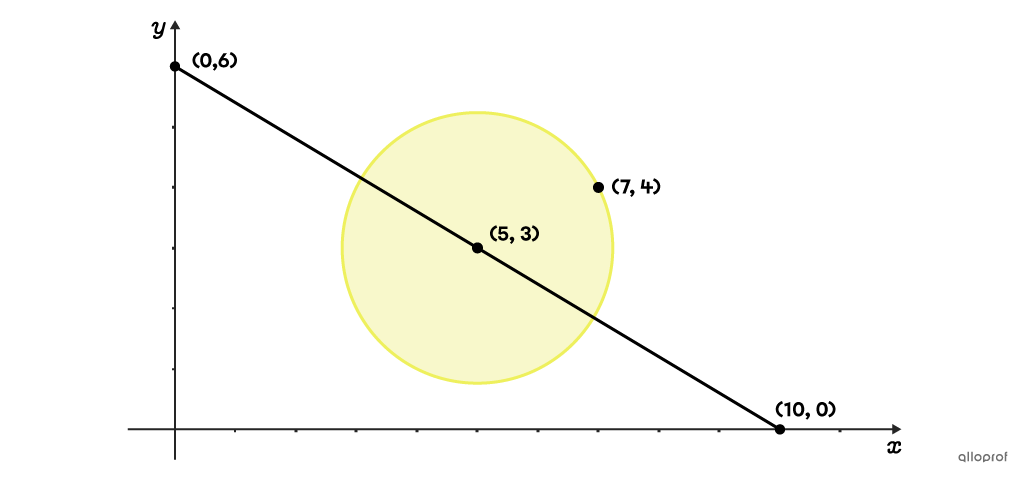
The desired probability involves a ratio of lengths.
||P(\text{circle}) = \dfrac{\text{Diameter of Circle}}{\text{Length of Segment}}||
First, we calculate the length of the segment using the formula for the distance between 2 points using the points |(0,6)| and |(10,0).|
||\begin{align}d&=\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\\&=\sqrt{(10 - 0)^2 + (0 - 6)^2}\\&=\sqrt{100+36}\\&=\sqrt{136}\\&\approx11.66\end{align}||
The total length of the segment is about |11.66| units.
Next we need to find the length of the circle's diameter. This can be done by finding the measure of its radius using the points |(5,3)| and |(7,4).|
||\begin{align}d&=\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\\&=\sqrt{(7 - 5)^2 + (4 - 3)^2}\\&=\sqrt{2^2 + 1^2}\\&=\sqrt{5}\\&\approx2.24\end{align}||
Since the radius measures approximately |2.24| units, the diameter measures |2.24 \times 2 = 4.48| units.
We can now calculate the probability.
||\begin{align}P(\text{circle})&= \dfrac{\text{Diameter of the Circle}}{\text{Length of Segment}}\\ &=\dfrac{4.48}{11.66}\\&\approx0.38\end{align}||
The probability that a randomly chosen point on the segment is also inside the circle is approximately |0.38,| or |38\%.|