Conditional probability is the probability that an event |B| occurs given that an event |A| has already occurred. It is denoted by |P(B \vert A).|
There are several ways to determine such a probability depending on the mode of representation used.
It is possible to calculate conditional probability using a tree diagram. To do so, simply find the correct probability in the tree.
We place |7| marbles in a container. There are |4| green marbles |(G)| and |3| orange marbles |(O).| We randomly pick |2| marbles without replacement. What is the probability of drawing an orange marble, given that a green marble was drawn on the 1st pick?
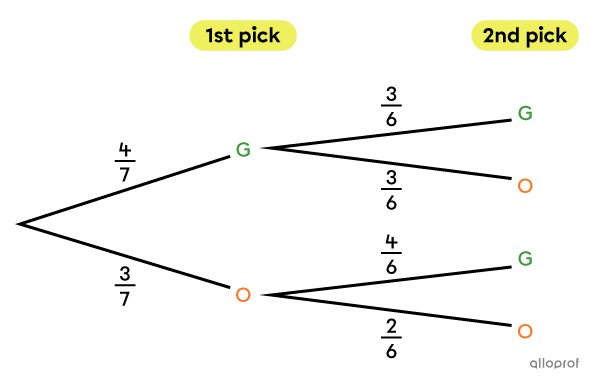
Since we know that a green marble was drawn on the 1st pick, the probability we are interested in is situated in the upper part of the diagram. We are therefore only interested in the 2 branches of the 2nd pick to answer the question. The probability of obtaining an orange marble on the 2nd pick is |\dfrac{3}{6},| or |\dfrac{1}{2}.|
Answer: The probability of drawing an orange marble given that a green marble was drawn on the 1st pick is |P(G\vert O)=\dfrac{1}{2}=50\ \%.|
It is also possible to calculate conditional probability using a table (double entry table).
Here is a study conducted at a movie theatre. It focuses on the types of movies preferred by men and women. The choices are divided into 2 categories: comedy movies and horror movies.
|
|
Comedy |
Horror |
Total |
|---|---|---|---|
|
Men |
23 |
67 |
90 |
|
Women |
75 |
24 |
99 |
|
Total |
98 |
91 |
189 |
Given that the person chosen is a man, what is the probability they prefer a comedy movie? To find the probability we need only look at the Men’s row in the table, since we know that the person is a man. There are |23| men who prefer comedy movies out of a total of |90| men.
Answer: The probability that a person's favourite movie type is comedy, given that the person is a man, is |P(\text{Comedy}\vert \text{Man})=\dfrac{23}{90}\approx 26\ \%.|
When the data is presented in a Venn diagram or without a mode of representation, it is less intuitive to find conditional probability. Instead, a formula is used to calculate the probability of an event |B| given that event |A| has already occurred.
|P(B \vert A)=\dfrac{P(B \cap A)}{P(A)}|
where
|P(B \cap A):| Intersection of events |B| and |A|
|P(A)>0|
We are interested in the probability of drawing a red card from a 52-card deck given that the card drawn is a diamond. The events are as follows:
|A:| getting a diamond card
|B:| getting a red face card
So, we want to find |P(B \vert A).|
We will represent this situation using a Venn Diagram.
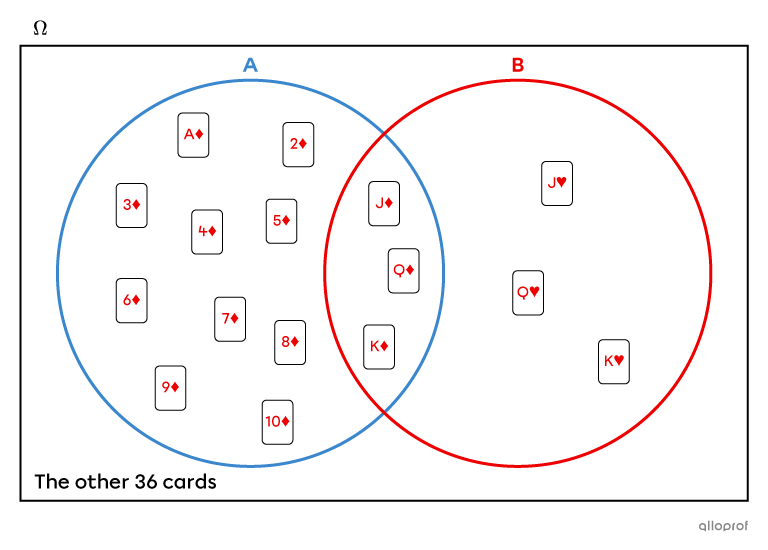
The formula |P(B \vert A) = \dfrac{P(B \cap A)}{P (A)}| is used.
The probability of being in the intersection |(B \cap A)| is |\dfrac{3}{52},| because there are only |3| cards out of |52| that are in both sets at the same time: the king, queen and jack of diamonds.
The probability of belonging to set |A| is |\dfrac{13}{52}|, because there are |13| diamond cards in the deck.
||\begin{align}P(B \vert A)&=\dfrac{P(B \cap A)}{P (A)}\\&=\dfrac{\ \ \dfrac{3}{52}\ \ }{\dfrac{13}{52}}\\&=\dfrac{3}{52} \times \dfrac{52}{13}\\&=\dfrac{3}{13}\end{align}||
Answer: Given that the card drawn was a diamond, the probability of drawing a red face card is |\dfrac{3}{13},| or about |23\ \%.|
Here is a Venn diagram that shows the number of students who must retake an exam in any of the following subjects: math, French, and/or English.
The events are as follows:
|M:| retake their math exam
|F:| retake their French exam
|E:| retake their English exam
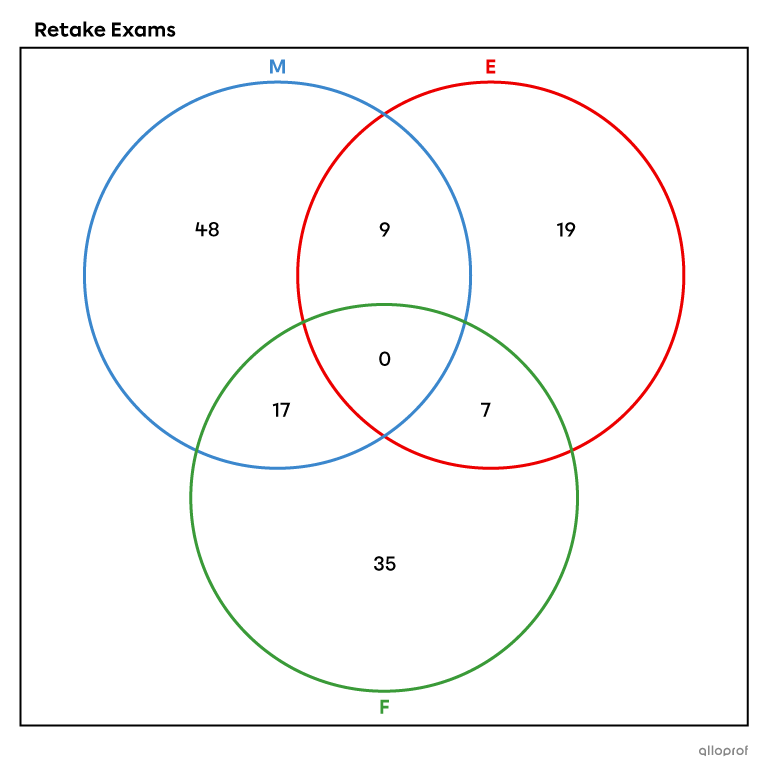
We want to know what the probability is that a student will retake their math exam given that they are retaking their French exam.
We are looking for the probability of |M| given |F,| or |P(M \vert F).|
We need to know |P(M \cap F)| and |P(F).| We’ll begin by finding the total number of students.
||48+9+19+17+7+35=135||
The probability of a student retaking the math exam and the French exam is |P(M \cap F).| This probability is |\dfrac{17}{135},| since there are |17| students in the intersection out of a total of |135| students.
We also need to find |P(F).| The probability is |\dfrac{59}{135},| because the set |F| has |59| students out of the |135| students total. We can now calculate the conditional probability.
||\begin{align}P(M \vert F)&=\dfrac{P(M \cap F)}{P(F)}\\ &= \dfrac{\ \ \dfrac{17}{135}\ \ }{\ \ \dfrac{59}{135}\ \ }\\ &= \dfrac{17}{135} \times \dfrac{135}{59}\\ &=\dfrac{17}{59}\end{align}||
Answer: The probability that a student retakes their math exam given that they are retaking their French exam is |\dfrac{17}{59},| or approximately |29\ \%.|
Consider a random experiment with events |A| and |B.| We know that |P(A)=0.4,| |P(B)=0.7| and |P(A \cap B)=0.2.| Calculate |P(A \vert B)| and |P(B \vert A).|
To calculate the 1st conditional probability, we use the formula.
||\begin{align}P(A \vert B) &= \dfrac{P(A \cap B)}{P(B)}\\ &=\dfrac{0.2}{0.7}\\ &\approx 0.29\end{align}||
To calculate the 2nd conditional probability, we use the same formula. It is important to note that the intersection is commutative, so |P(A \cap B) = P(B \cap A).|
||\begin{align}P(B \vert A) &= \dfrac{P(B \cap A)}{P(A)}\\ &=\dfrac{0.2}{0.4}\\ &= 0.5\end{align}||
Answer: ||\begin{align}P(A \vert B) &\approx 0.29 \\\\ P(B \vert A) &= 0.50\end{align}||
It is also possible to answer other questions related to the information in the previous question.
To answer this question, remember that 2 events are independent if |P(A \cap B) = P(A) \times P(B).|
It is sufficient to check whether this condition is met.
||\begin{align}P(A \cap B) &\overset{?}{=} P(A) \times P(B)\\0.2 &\overset{?}{=} 0.4 \times 0.7\\0.2 &\neq0.28 \end{align}||
Since the condition is not met, we conclude that events |A| and |B| are dependent.
To answer this question, remember that 2 events |(A| and |B)| are mutually exclusive if |P(A \cap B)=0.| This implies that |P(B \vert A)=0.| However, this is not the case therefore we conclude that events |A| and |B| are non-mutually exclusive.
Consider a random experiment with events |A| and |B.| We know that |P(B \vert A)=0.25| and |P(B \cap A)=0.2.| Calculate |P(A).|
We use the formula and isolate |P(A).|
||\begin{align}P(B \vert A) &= \dfrac{P(B \cap A)}{P(A)}\\ 0.25&=\dfrac{0.2}{P(A)}\\ P(A)&= \dfrac{0.2}{0.25}\\P(A)&=0.8\end{align}||
Answer: The probability of event |A| is |0.8.|