Sometimes the question refers to the probability of 2 possible choices in a random experiment. Depending on the wording of the question, there are 2 possible calculations.
-
If the probability of one choice or another is sought, the probabilities of each possible choice are added together.
-
If the probability of one choice and another choice is sought, the probabilities of each possible choice are multiplied.
In a one-step or multi-step random experiment, the probabilities must be added together when looking at one choice or another. In a tree diagram, this is represented by two branches at the same step.
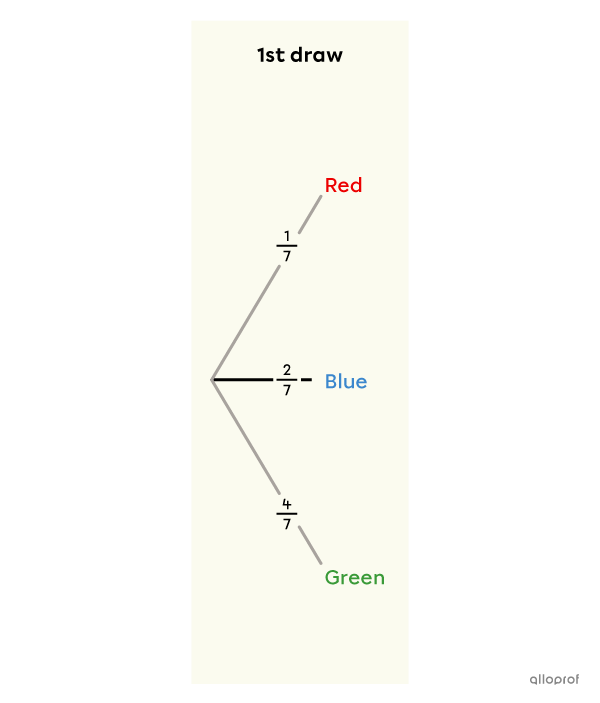
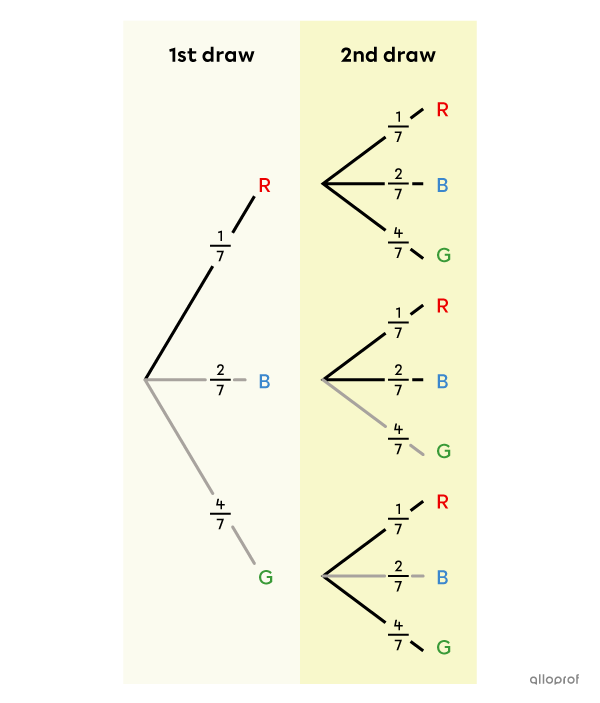
A marble is drawn from a bag containing |1| red marble, |2| blue marbles and |4| green marbles. What is the probability of the event "drawing a red marble or a green marble"?
A tree diagram is constructed.
In this one-step random experiment, the event involves 2 possible choices. To find the probability of the event, the probabilities of these two choices must be added together.
||\begin{align}P(\text{Red or Green})&=P(\text{Red})+P(\text{Green})\\&= \dfrac{1}{7} + \dfrac{4}{7}\\&= \dfrac{5}{7}\end{align}||
Answer: The probability of drawing a red marble or a green marble is |\dfrac{5}{7},| or about |71\ \%.|
Sometimes the word "or" is not included in the statement of an event, but you still need to add the probabilities to find the probability you are looking for.
A |6|-sided die is rolled. What is the probability of the event "getting a prime number"?
The prime numbers on a 6-sided die are |2,| |3| and |5.| So, this amounts to finding the probability of the event "getting a |2| or a |3| or a |5|."
||\begin{align}P(\text{Prime Number})&=P(\text{Getting a}\ 2)+P(\text{Getting a}\ 3)+P(\text{Getting a}\ 5)\\&= \dfrac{1}{6} + \dfrac{1}{6} +\dfrac{1}{6}\\&= \dfrac{3}{6}\\&=\dfrac{1}{2}\end{align}||
Answer: The probability of getting a prime number is |\dfrac{1}{2},| or |50\ \%.|
In a Venn diagram, the notion of "or" is associated with the union of sets. To determine which elements are part of either |A| or |B,| we must look at |A \cup B.| The elements that are only part of |A,| the elements that are only part of |B,| and the elements that are part of the intersection of |A| and |B| |(A \cap B)| must all be counted.
In a class of |32| students, |12| play only hockey, |7| play only baseball, and |4| play both hockey and baseball. The other students in the class play other sports. If a student is chosen at random, what is the probability that they play hockey or baseball?
The Venn diagram associated with this situation is constructed.
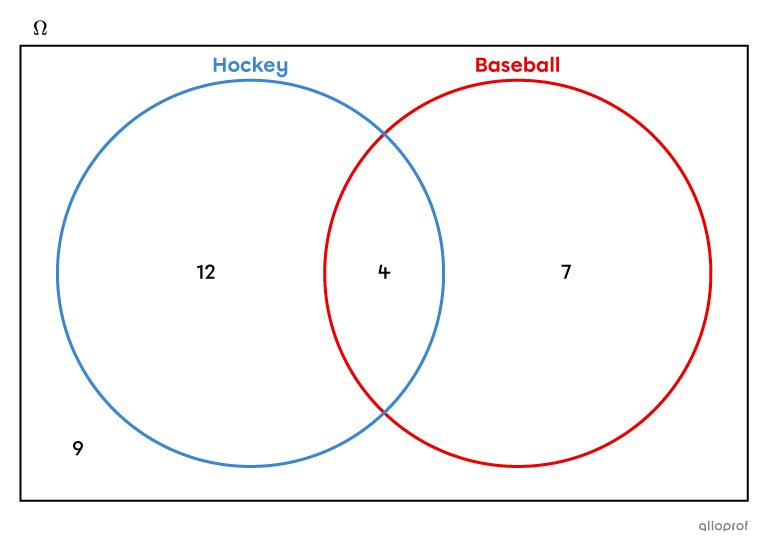
To find the probability of randomly selecting a student who plays hockey or baseball, the number of students who play only hockey, who play only baseball and who play both sports must be added together.
||\begin{align}P(\text{Hockey or Baseball})&=\dfrac{12+4+7}{32}\\&=\dfrac{23}{32}\\&\approx 0.72\end{align}||
Answer: The probability of randomly selecting a student who plays hockey or baseball is |\dfrac{23}{32},| or about |72\ \%.|
In a multi-step random experiment, the probabilities must be multiplied when we are interested in one choice followed by another. In a tree diagram, this situation is represented by 2 branches end to end.
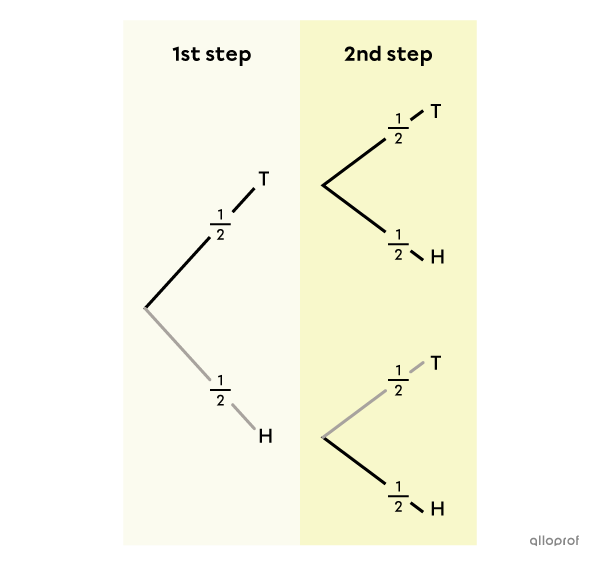
A coin is flipped twice. What is the probability of getting "heads" (H) and "tails" (T), if the order matters?
The tree diagram is constructed.
This is a 2-step experiment. We are looking for |P(\text{H},\text{T}).| The probability of getting "heads" on the first roll is multiplied by the probability of getting "tails" on the second.
||\begin{align}P(\text{H},\text{T})&=\dfrac{1}{2} \times \dfrac{1}{2}\\ &= \dfrac{1}{4}\end{align}||
Answer: The probability of getting "heads" on the 1st roll and "tails" on the 2nd is |\dfrac{1}{4},| or |25\ \%.|
The use of the word "and" can have several meanings, depending on whether or not the order matters in the random experiment. It is therefore important to analyze the question carefully in order to answer it properly.
In the previous example, if we were interested in the same event, but the order did not matter, the answer would have been different. Instead, both |(\text{F},\text{P})| and |(\text{P},\text{F})| would have been favourable outcomes for that event. We would then have to find the probability of these |2| outcomes, and add them together.
A bag contains |1| red marble |(R),| |2| blue marbles |(B)| and |4| green marbles |(G).|
|1| marble is drawn from this bag and then replaced. A second marble is then drawn.
What is the probability of the event "drawing one blue and one green marble " if the order does not matter?
The tree diagram is constructed.
To find the probability of this event, we start by finding the probability of drawing a blue marble followed by a green marble and the probability of drawing a green marble followed by a blue marble.
||\begin{align}P(B,G)&=P(B) \times P(G)\\&= \dfrac{2}{7} \times \dfrac{4}{7}\\&= \dfrac{8}{49}\\\\P(G,B)&=P(G) \times P(B)\\&= \dfrac{4}{7} \times \dfrac{2}{7}\\&= \dfrac{8}{49}\end{align}||
These 2 probabilities are then added together.
||\begin{align}P(B\text{ and }G)&=P(B,G)+P(G,B)\\&=\dfrac{8}{49}+\dfrac{8}{49}\\&=\dfrac{16}{49}\end{align}||
Answer: The probability of drawing a blue marble and a green marble is |\dfrac{16}{49},| or about |33\ \%.|
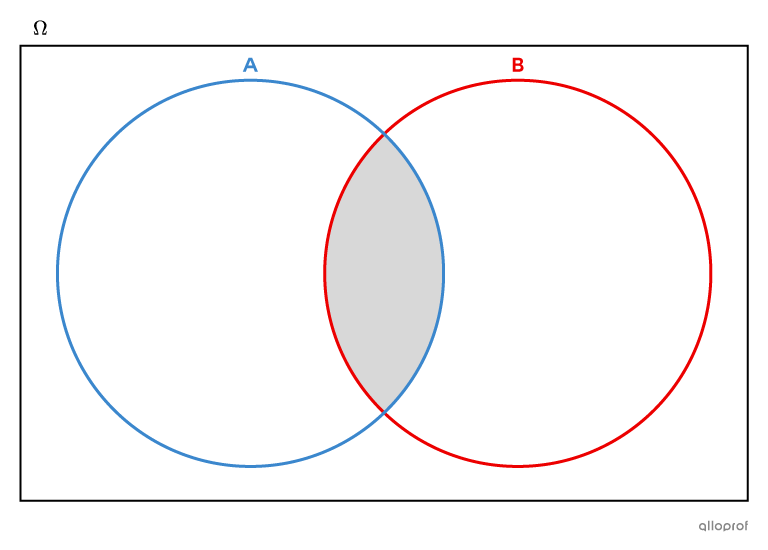
In a Venn diagram, the notion of "and" is associated with the intersection. Specifically, to determine which elements are part of |A| and |B,| we must look at |A \cap B.|
In a class of |32| students, |12| play only hockey, |7| play only baseball and |4| play both hockey and baseball. The other students in the class play other sports. If a student is chosen at random, what is the probability that they play hockey and baseball?
The Venn diagram associated with this situation is constructed.
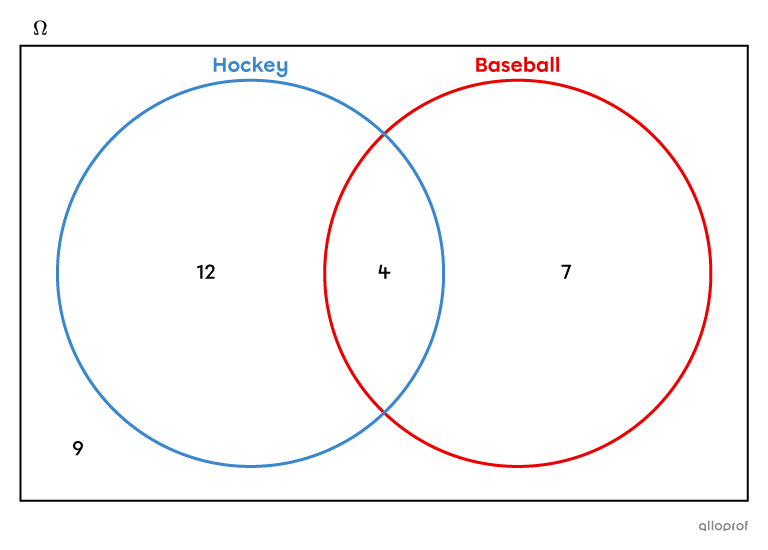
To find the probability of randomly selecting a student who plays hockey and baseball, the intersection of the sets must be taken into account, i.e. only those students who play both sports.
||\begin{align}P(\text{Hockey and Baseball})&=\dfrac{4}{32}\\&=\dfrac{1}{8}\end{align}||
Answer: The probability of randomly choosing a student who plays hockey and baseball is |\dfrac{1}{8},| or |125\%.|
To answer a question, one may need to use the concepts of both "and" and "or." When this occurs, we would first use multiplication to calculate the probability of a specific outcome of a multi-step random experiment, and then use addition to add the probabilities of certain outcomes together.
Two roulette wheels are spun. The 1st wheel is separated into |3| parts, identified by the numbers |1| to |3.| The 2nd wheel is separated into |4| parts, identified by the letters |A,| |B,| |C| and |D.|
On the 1st roulette wheel, section |1| and section |2| each occupy a quarter of the wheel, while section |3| occupies half. On the second roulette wheel, sections |A| and |C| each occupy a quarter of the wheel, section |B| occupies an eighth and section |D| occupies |3| eighths of the wheel.

What is the probability of getting |1| and |A| or getting |3| and |D|?
-
Construct the tree diagram that represents the situation
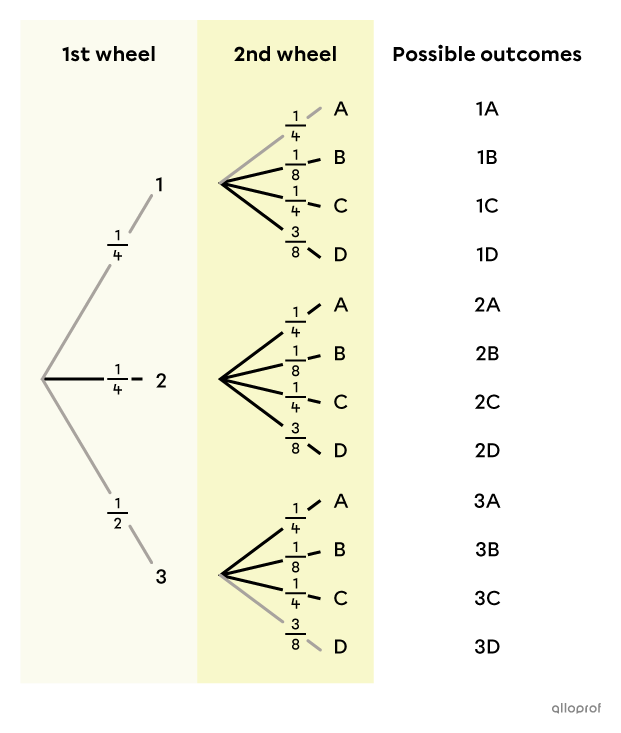
-
Calculate the probability of each outcome of interest
Multiplication is used for this.||\begin{align}P(1,A)&=\dfrac{1}{4}\times \dfrac{1}{4}=\dfrac{1}{16}\\P(3,D)&=\dfrac{1}{2}\times \dfrac{3}{8}=\dfrac{3}{16}\end{align}|| -
Add the probabilities
Since we are looking for the probability of getting |(1,A)| or getting |(3,D),| we add the two previously calculated probabilities.||\begin{align}P\big((1,A)\text{ or }(3,D)\big)&=P(1,A)+P(3,D)\\&=\dfrac{1}{16}+\dfrac{3}{16}\\&=\dfrac{4}{16}\\&=\dfrac{1}{4}\end{align}||
Answer: The probability of getting |(1,A)| or |(3,D)| is |\dfrac{1}{4},| or |25\ \%.|