Vectors are used to model the physical world around us. Examples for applying vectors in this concept sheet are situations sometimes seen in math textbooks for Secondary V SN and TS, but in reality, they are concepts applied to physics. The following situations will be covered in this concept sheet:
When several forces act upon the same object, all of them can be replaced with the resultant force (|F_R|).
The resultant force is calculated by using vector addition on all of the forces present. The object will react in the same way when we apply all the forces as when we apply the resultant force.
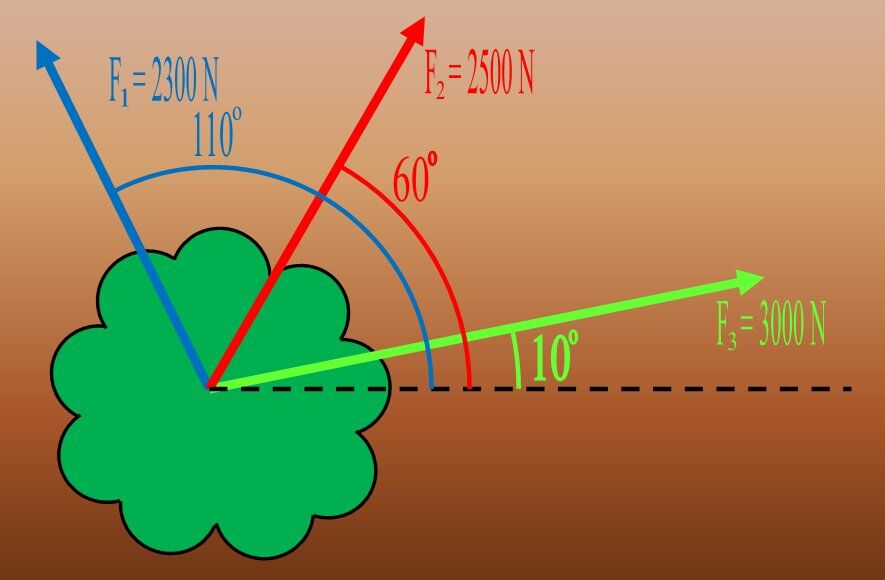
Three horses pull on a tree as shown below. Each horse is represented by a force: |F_1,F_2| and |F_3| . To avoid an accident, in which direction should the tree fall?
-
Find the components of each of the vectors
Using the trigonometric ratios for right triangles, the following components can be determined: ||\begin{align} \color{blue}{F_1 (x,y)} & \\
\Rightarrow \color{blue}{x} &= 2 \ 300 \cos 110^\circ \\
&= - 787\ \text{N} \\
\Rightarrow \color{blue}{y} &= 2 \ 300 \sin 110^\circ \\
&= 2 \ 161\ \text{N}\\
\color{red}{F_2 (x,y)} &\\
\Rightarrow \color{red}{x} &= 2 \ 500 \cos 60^\circ \\
&= 1 \ 250\ \text{N}\\
\Rightarrow \color{red}{y} &= 2 \ 500\sin 60^\circ \\
&= 2 \ 165\ \text{N}\\
\color{green}{F_3 (x,y)} &\\
\Rightarrow \color{green}{x} &= 3 \ 000 \cos 10^\circ \\
&= 2 \ 954\ \text{N}\\
\Rightarrow \color{gree}{y} &= 3 \ 000\sin 10^\circ \\
&= 521\ \text{N}\end{align}|| -
Add the components to obtain those of the |F_R|
|x| |y| |\color{blue}{F_1}| |- 787\ \text{N}| |2 \ 161\ \text{N}| |\color{red}{F_2}| |1 \ 250\ \text{N}| |2 \ 165\ \text{N}| |\color{green}{F_3}| |2 \ 954\ \text{N}| |521\ \text{N}| |F_R| | 3 \ 417\ \text{N}| |4 \ 847\ \text{N}| -
Calculate |\mid \mid F_R \mid \mid|
||\begin{align}\mid \mid F_R \mid \mid &= \sqrt{3 \ 417^2 + 4 \ 847^2} \\
&\approx 5 \ 930\ \text{N} \end{align}|| -
Determine the orientation of |F_R|
A right triangle is formed by representing the components of |F_R| in a Cartesian plane. It enables the use of trigonometric ratios.
||\begin{align}\tan \theta &= \displaystyle \frac{4 \ 847}{3 \ 417}\\
&\approx 55^\circ \end{align}|| -
Interpret the answer
Thus, the tree should fall at an angle of |55^\circ| with a positive |x|-axis.
In this example, it was not essential to find the norm (magnitude) of |F_R|. If necessary, this part of the example can be used as a reference.
The balanced force, sometimes written (|F_É|), is the force that must be added to a sum of forces so that they (including the balancing force) are equal to zero. Therefore, we can say the balanced force is equal to the resultant force with an opposite direction.
Depending on the information available, two different methods can be used to change the direction of the resultant force.
-
If the vector is given with its norm and its orientation, it will be necessary to add |180^\circ| to (or subtract |180^\circ| if the orientation is |180^\circ| or more) and the norm remains the same.
-
If the vector is given with its components, change the sign of each of the components.
To simplify this concept sheet, we will use the previous example.
To prevent the tree from falling immediately, we must apply a sufficient counterbalance. What should be the components of the balanced force?
-
Find the components of the resultant force.
As calculated in the example above,
||F_R = (3 \ 417, 4 \ 847)|| -
Determine the components of the balanced force.
||\begin{align} F_R &= (3 \ 417 , 4 \ 847) \\
\Rightarrow F_É &= (-3 \ 417, -4 \ 847)\end{align}||
Using an example referring to the norm and orientation of |F_R|, simply add or subtract |180^\circ| while ensuring the orientation of |F_É| is positive.
For more details and explanations about the concept of forces, see the following concept sheet in Physics: Forces.
The displacement vector is the difference between two position vectors, as follows: |\overrightarrow{r_f}| is the final position and |\overrightarrow{r_i}| is the initial position.
Note |\Delta \overrightarrow{r}| is the displacement vector.
In other words, we can associate the concept with the resultant vector.
Consider the following diagram:

The displacement vector corresponds to
||\Delta \overrightarrow{r} = \overrightarrow{r_f}-\overrightarrow{r_i}||
To determine the components of |\color{red}{\Delta \overrightarrow {r}}|, refer to Vector Subtraction.
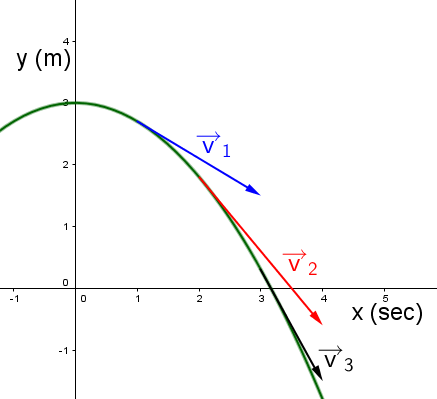
The velocity vector is the ratio between the displacement vector and the elapsed time. Such a vector has a horizontal component (horizontal velocity) and a vertical component (vertical velocity).
In the following diagram, the vectors |\color{blue}{\overrightarrow{v_1}}, \color{red}{\overrightarrow{v_2}}| and |\overrightarrow{v_3}| are velocity vectors.
||W= F \times \Delta x||
where |W| is the work done (in J), |F| is the applied force (in N) and |\Delta x| is the magnitude of the displacement (in m).
In this context, the application of vectors is rather banal since the work done by the person is directly applied to the load. Thus, it is more interesting to analyze the work done when the force exerted on the load is not parallel to the displacement.
||W = F \cos \theta \times \Delta x||
where |W| is the work done (in J), |F \cos \theta| is the component of the force parallel to the displacement (in N), |\theta| is the angle between the force vector and the displacement vector and |\Delta x| is the displacement (in m).
Thus, take the time to properly analyze the situation and draw a diagram to associate each of the measures with the situation’s different components.
The fateful date of July 1st is approaching, and Bill has to move his furniture into his new apartment. His washer is too heavy to lift, so he decides to tie a rope to it and pull it.
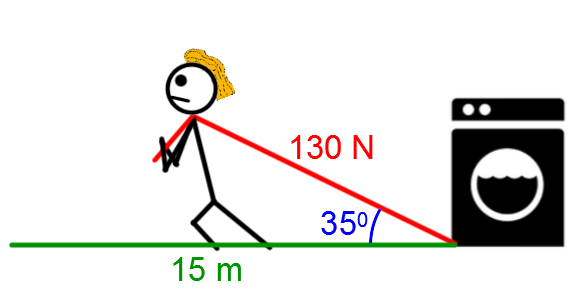
What work will Bill have to expend to move the washer a distance of 15 m, if he applies a force of |130 \ N| and the rope he is using is at a |35^\circ| angle relative to the horizontal, while overlooking the amount of friction?
-
Analyze the situation
In this case, the work done is not parallel to the displacement vector. So, use the formula
||W = F \cos \theta \times \Delta x|| -
Apply the appropriate formula
The angle measurement is composed by the force vector and the displacement vector, thus, use the following formula:
||\begin{align} W &= \color{red}{F} \cos \color{blue}{\theta} \times \color{green}{\Delta x}\\
&= \color{red}{130} \cos \color{blue}{35^\circ} \times \color{green}{15}\\
&\approx 1\ 597 \ \text{J} \end{align}|| -
Interpret the answer
Bill will have to exert |1\ 597| joules to move his washer.
On the other hand, the angle formed by the force vector and the displacement vector is not always provided.
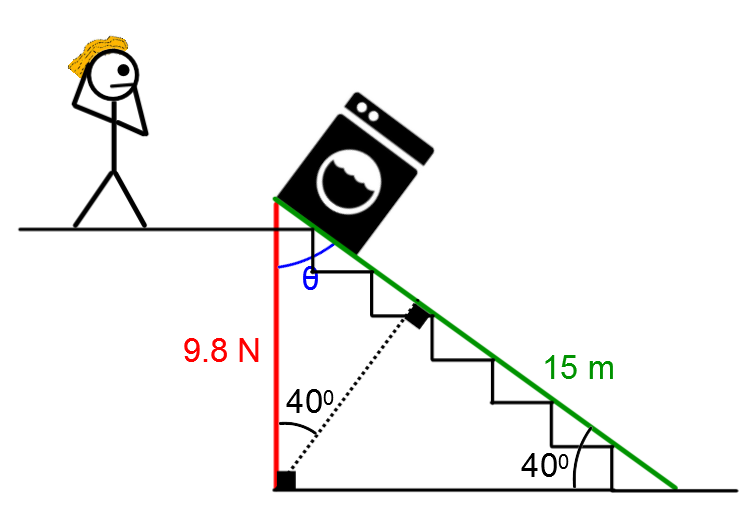
When he reaches the stairs, Bill decides to put down a board with a length of 15 m to create an incline. Thus, the force of gravity (approximately |9{.}8\ \text{N}|) will enable the washer to slide safely to the bottom of the stairs. Ignoring the frictional force, what will be the real work performed by gravitational force if the incline on the stairs is |40^\circ|?
-
Analyze the situation
Due to the presence of similar triangles, we can determine the measure of the angle of |40^\circ| in two places. To apply the formula, obtain the value of |\color{blue}{\theta}|. Since the sum of the interior angles of a triangle is equal to |180^\circ|, we determine the following:||\begin{align} \color{blue}{\theta} &= 180^\circ - 40^\circ - 90^\circ \\
&= 50^\circ \end{align}|| -
Apply the appropriate formula
||\begin{align}W &= \color{red}{F} \cos \color{blue}{\theta} \times \color{green}{\Delta x}\\
&= \color{red}{9{,}8} \cos \color{blue}{50^\circ} \times \color{green}{15}\\
& \approx 104\ J \end{align}|| -
Interpret the answer
Gravitational force will do about 104 joules of work to slide Bill's washer down.
Note: There are several different ways to resolve this kind of problem. In this case, the aim was to show how to use the formula presented at the beginning of the section. However, one can arrive at the same answer by using concepts in the concept sheet Work and Power, which is located in the Physics section of the virtual library.
To Validate your understanding of vectors, consult the following interactive CrashLesson:
