The Inverse of the Exponential Function

1. Interchange |x| and |y.|

2. Isolate the |y| variable to get the inverse function.

3. Give the rule of the inverse.

The exponential function has a horizontal asymptote at |y=k,| limiting its range. Therefore, its inverse, the logarithmic function, has a vertical asymptote at |x=h,| limiting its domain.

Determine the rule of the inverse of the function |f(x)=2(3)^{3x}.|

1. Interchange |x| and |y|
   ||\begin{align}\color{#ff55c3}y&=2(3)^{3\color{#3a9a38}x}\\\color{#3a9a38}x&=2(3)^{3\color{ #ff55c3}y}\end{align}||

2. Isolate the |y| variable
   Start by isolating the power:
   ||\dfrac{x}{2}=3^{3\color{#ff55c3}y}||
   We switch to the logarithmic form.||\color{#EC0000}{\dfrac {x}{2}}=\color{#51B6C2}3^{\color{#7CCA51}{3y}}\\\Updownarrow\\\color{#7CCA51}{3y}=\log_{\color{# 51B6C2}3}\left(\color{#EC0000}{\dfrac{x}{2}}\right)||
   Isolate |y|:
   ||\begin{align}3\color{#ff55c3}y&= \log_3\!{\left(\dfrac{x}{2}\right)}\\\color{#ff55c3}y&=\dfrac{1}{3}\log_3\!{\left(\dfrac{x }{2}\right)}\end{align}||

3. Give the rule of the inverse
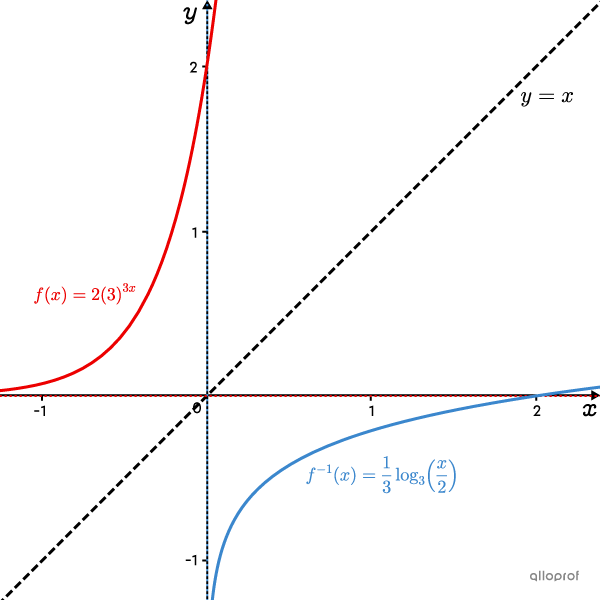
   The inverse of the function |f(x)=2(3)^{3x}| is |f^{-1}(x)=\dfrac{1}{3}\log_3{\left(\dfrac{x}{2}\right)}|

The following graph that shows the function |\color{#ec0000}{f(x)}| and its inverse, |\color{#3b87cd}{f^{-1}(x)}.|

Determine the rule of the inverse of the function |f(x)=-2(4)^{-\frac{1}{3}(x+5)}-7|

1. Interchange |x| and |y|
   ||\begin{align}\color{#ff55c3}y&=-2(4)^{-\frac{1}{3}(\color{#3a9a38}x+5)}-7\\ \color{#3a9a38}x&=-2(4)^{-\frac{1}{3}(\color{#ff55c3}y+5)}-7\end{align}||

2. Isolate the |y| variable
   
   Start by isolating the power:
   ||\begin{align}x&=-2(4)^{-\frac{1}{3}(\color{#ff55c3}y+5)}-7\\ x+7&=-2(4)^{-\frac{1}{3}(\color{#ff55c3}y+5)}\\-\dfrac{1}{2}(x+7)&=4^{-\frac{1}{3}(\color{#ff55c3}y+5)}\end{align}||
   Switch to logarithmic form:
   ||\color{#EC0000}{-\dfrac{1}{2}(x+7)} = \color{#51B6C2}4^{\color{#7CCA51}{-\frac{1}{3}(y+5)}}\\ \Updownarrow\\ \color{#3A9A38}{\color{#7CCA51}{-\frac{1}{3}(y+5)}} = \log_{\color{#51B6C2}4}\left(\!\color{#EC0000}{-\dfrac{1}{2}(x+7)}\!\right)||

Isolate |y.| ||\begin{align}-\dfrac{1}{3}(\color{#ff55c3}y+5)&=\log_ {4}\left(-\dfrac{1}{2}(x+7)\right)\\\color{#ff55c3}y+5&=-3\log_ {4}\left(-\dfrac{1}{2}(x+7)\right)\\\color{#ff55c3}y&=-3\log_ {4}\left(-\dfrac{1}{2}(x+7)\right)-5\end{align}||

3. Give the rule of the inverse
   
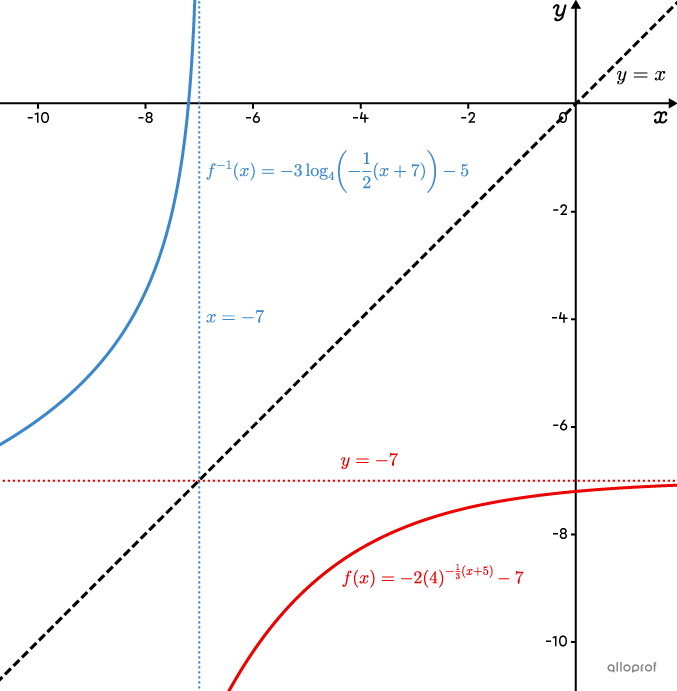
   The inverse of the function |f(x)=-2(4)^{-\frac{1}{3}(x+5)}-7| is |f^{-1}(x)=-3\log_{4}\left(\!-\dfrac{1}{2}(x+7)\!\right)-5|
   
   The following is the graph that shows the function |\color{#ec0000}{f(x)}| and its inverse, |\color{#3b87cd}{f^{-1}(x)}|

​It is possible to sketch the inverse of a function by interchanging the coordinates |x| and |y| of certain points.

For example, in the following figure, we can study the function |\color{#EC0000}{f(x)=\dfrac{3}{2}(2)^{x-5}-2}| and its inverse, |\color{#3B87CD}{f^{-1}(x)=\log_2\left(\dfrac{2}{3}(x+2)\right)+5}.|

• The y-intercept of |\color{#EC0000}{f(x)}| becomes the x-intercept of |\color{#3B87CD}{f^{-1}(x)}.|||\color{#EC0000}{(0,-1{.}95)}\ \rightarrow\ \color{#3B87CD}{(-1{.}95,0)}||

• The x-intercept of |\color{#EC0000}{f(x)}| becomes the y- intercept of |\color{#3B87CD}{f^{-1}(x)}|||\color{#EC0000}{(5{.}42,0)}\ \rightarrow\ \color{#3B87CD}{(0,5{.}42)}||

• Point |\color{#EC0000}{(7,4)}| becomes the point |\color{#3B87CD}{(4,7)}.|

The same is true for the asymptote. The horizontal asymptote of |\color{#EC0000}{f(x)}| becomes the vertical asymptote of |\color{#3B87CD}{f^{-1}(x)}.|
||\color{#EC0000}{y=-2}\ \rightarrow\ \color{#3B87CD}{x=-2}||

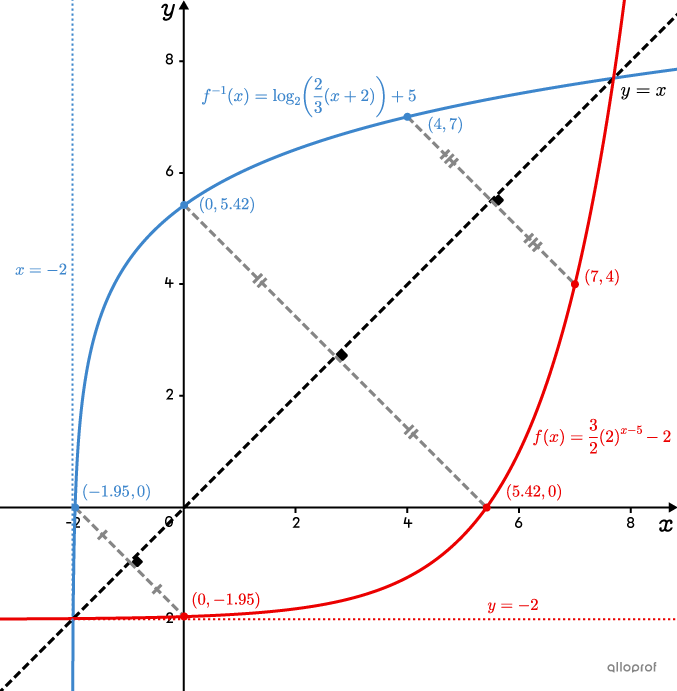
We can also say that |\color{#3B87CD}{f^{-1}(x)}| corresponds to the reflection of |\color{#EC0000}{f(x)}| with respect to the line |y=x.| It is therefore possible to graph the inverse by reflection, if the scale of the |x| and |y| axes have a ratio of |1:1.|