La réciproque d’une fonction exponentielle est une fonction logarithmique.
Voici les étapes à suivre pour trouver la règle de la réciproque d’une fonction exponentielle dont on connait la règle.
-
Interchanger |x| et |y.|
-
Isoler la variable dépendante |y| pour obtenir la fonction réciproque.
-
Donner la règle de la réciproque.
La fonction exponentielle a une asymptote horizontale à |y=k| qui limite son image. Ainsi, sa réciproque, la fonction logarithmique, a une asymptote verticale à |x=h| qui limite son domaine.
L'exemple suivant montre comment trouver la réciproque d'une fonction exponentielle sous la forme |f(x) = ac^{bx}.|
Détermine la règle de la réciproque de la fonction |f(x)=2(3)^{3x}.|
-
Interchanger |x| et |y|
||\begin{align}\color{#ff55c3}y&=2(3)^{3\color{#3a9a38}x}\\ \color{#3a9a38}x&=2(3)^{3\color{#ff55c3}y}\end{align}|| -
Isoler |y|
On commence par isoler la puissance.||\dfrac{x}{2}=3^{3\color{#ff55c3}y}||On passe à la forme logarithmique.||\color{#EC0000}{\dfrac{x}{2}}=\color{#51B6C2}3^{\color{#7CCA51}{3y}}\\\Updownarrow\\\color{#7CCA51}{3y}=\log_{\color{#51B6C2}3}\left(\color{#EC0000}{\dfrac{x}{2}}\right)||On isole |y.|||\begin{align}3\color{#ff55c3}y&=\log_3\!{\left(\dfrac{x}{2}\right)}\\\color{#ff55c3}y&=\dfrac{1}{3}\log_3\!{\left(\dfrac{x}{2}\right)}\end{align}|| -
Donner la règle de la réciproque
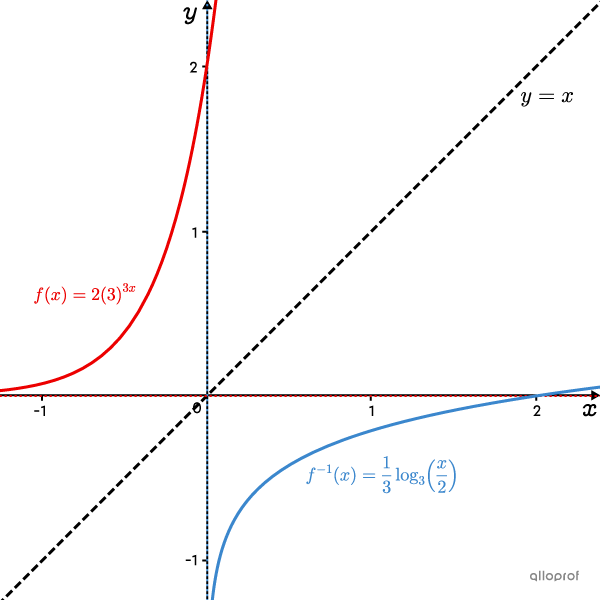
La réciproque de la fonction |f(x)=2(3)^{3x}| est |f^{-1}(x)=\dfrac{1}{3}\log_3{\left(\dfrac{x}{2}\right)}.|
Voici le graphique qui montre la fonction |\color{#ec0000}{f(x)}| et sa réciproque, |\color{#3b87cd}{f^{-1}(x)}.|
L'exemple suivant montre comment trouver la réciproque d'une fonction exponentielle sous la forme |f(x)=a(c)^{b(x-h)}+k.|
Détermine la règle de la réciproque de la fonction |f(x)=-2(4)^{-\frac{1}{3}(x+5)}-7.|
-
Interchanger |x| et |y|
||\begin{align}\color{#ff55c3}y&=-2(4)^{-\frac{1}{3}(\color{#3a9a38}x+5)}-7\\ \color{#3a9a38}x&=-2(4)^{-\frac{1}{3}(\color{#ff55c3}y+5)}-7\end{align}|| -
Isoler |y|
On commence par isoler la puissance.||\begin{align}x&=-2(4)^{-\frac{1}{3}(\color{#ff55c3}y+5)}-7\\ x+7&=-2(4)^{-\frac{1}{3}(\color{#ff55c3}y+5)}\\-\dfrac{1}{2}(x+7)&=4^{-\frac{1}{3}(\color{#ff55c3}y+5)}\end{align}||On passe à la forme logarithmique.||\color{#EC0000}{-\dfrac{1}{2}(x+7)} = \color{#51B6C2}4^{\color{#7CCA51}{-\frac{1}{3}(y+5)}}\\ \Updownarrow\\ \color{#3A9A38}{\color{#7CCA51}{-\frac{1}{3}(y+5)}} = \log_{\color{#51B6C2}4}\left(\!\color{#EC0000}{-\dfrac{1}{2}(x+7)}\!\right)||
On isole |y.| ||\begin{align}-\dfrac{1}{3}(\color{#ff55c3}y+5)&=\log_ {4}\left(-\dfrac{1}{2}(x+7)\right)\\\color{#ff55c3}y+5&=-3\log_ {4}\left(-\dfrac{1}{2}(x+7)\right)\\\color{#ff55c3}y&=-3\log_ {4}\left(-\dfrac{1}{2}(x+7)\right)-5\end{align}||
-
Donner la règle de la réciproque
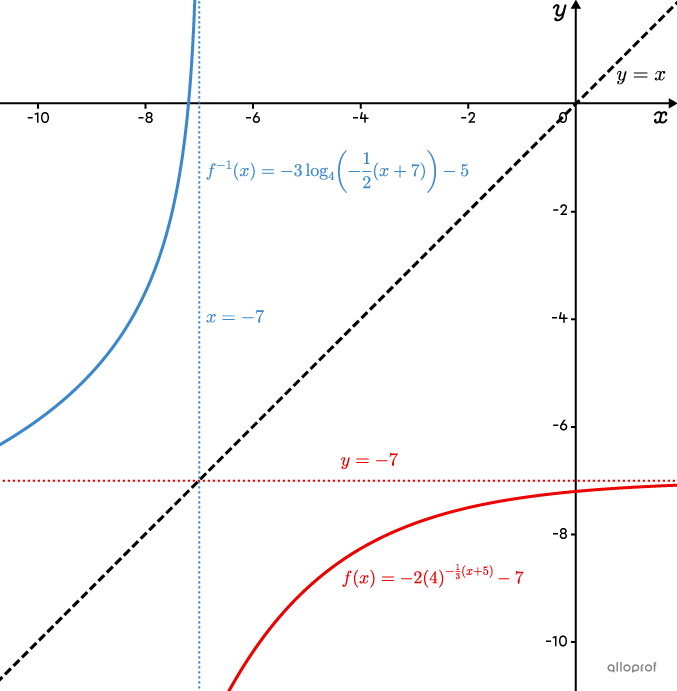
La réciproque de la fonction |f(x)=-2(4)^{-\frac{1}{3}(x+5)}-7| est |f^{-1}(x)=-3\log_{4}\left(\!-\dfrac{1}{2}(x+7)\!\right)-5.|
Voici le graphique qui montre la fonction |\color{#ec0000}{f(x)}| et sa réciproque, |\color{#3b87cd}{f^{-1}(x)}.|
Il est possible de tracer la réciproque d’une fonction en interchangeant les coordonnées |x| et |y| de certains points.
Par exemple, dans la figure ci-dessous, on peut observer la fonction |\color{#EC0000}{f(x)=\dfrac{3}{2}(2)^{x-5}-2}| et sa réciproque, |\color{#3B87CD}{f^{-1}(x)=\log_2\left(\dfrac{2}{3}(x+2)\right)+5}.|
-
L’ordonnée à l’origine de |\color{#EC0000}{f(x)}| devient l’abscisse à l’origine de |\color{#3B87CD}{f^{-1}(x)}.|||\color{#EC0000}{(0;-1{,}95)}\ \rightarrow\ \color{#3B87CD}{(-1{,}95;0)}||
-
L’abscisse à l’origine de |\color{#EC0000}{f(x)}| devient l’ordonnée à l’origine de |\color{#3B87CD}{f^{-1}(x)}.|||\color{#EC0000}{(5{,}42;0)}\ \rightarrow\ \color{#3B87CD}{(0;5{,}42)}||
-
Le point |\color{#EC0000}{(7,4)}| devient le point |\color{#3B87CD}{(4,7)}.|
Il en est de même pour l’asymptote. L’asymptote horizontale de |\color{#EC0000}{f(x)}| devient l’asymptote verticale de |\color{#3B87CD}{f^{-1}(x)}.| ||\color{#EC0000}{y=-2}\ \rightarrow\ \color{#3B87CD}{x=-2}||
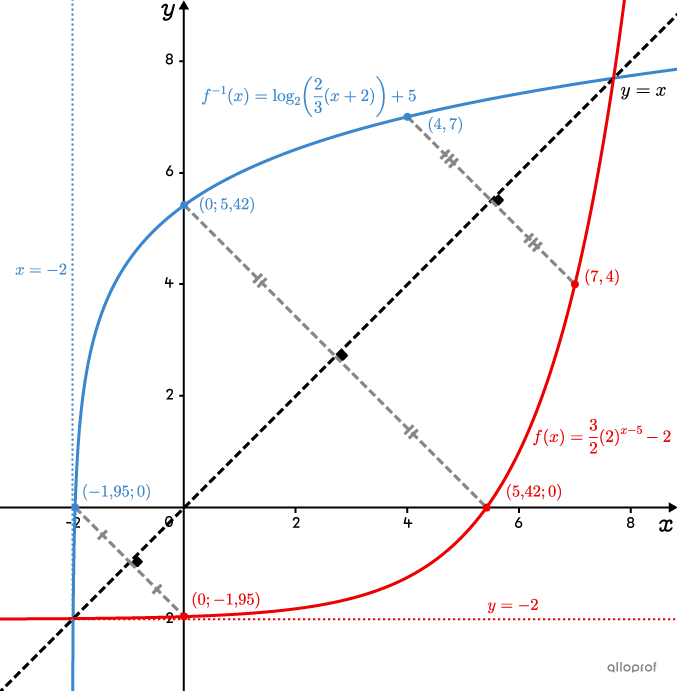
On peut aussi dire que |\color{#3B87CD}{f^{-1}(x)}| correspond à la réflexion de |\color{#EC0000}{f(x)}| par rapport à l’axe d’équation |y=x.| Il est donc possible de tracer la réciproque par réflexion à condition que la graduation des axes |x| et |y| soit dans un rapport |1:1.|