The inverse of a function |f| is obtained by inverting the values of |x| and |y,| then isolating |y.| The notation is |f^{-1}.|
The graph of an inverse is obtained by subjecting the function to a reflection with respect to the axis |y=x.|
Note: Often, |f^{-1}| is not written and |y=| is used instead.
Consider a function |f| that passes through the points |(-2,-4),(-1,-2),(0,0),(1,2),(2,4).|
Therefore, the inverse |f^{-1}| will go through the points |(-4,-2),(-2,-1),(0,0),(2,1),(4,2).|
The inverse of a function is not always a function.
The inverse of |f,| denoted as |f^{-1},| is a function if and only if no horizontal line (parallel to the |x|-axis) intersects the graph of the function |f| at more than one point.
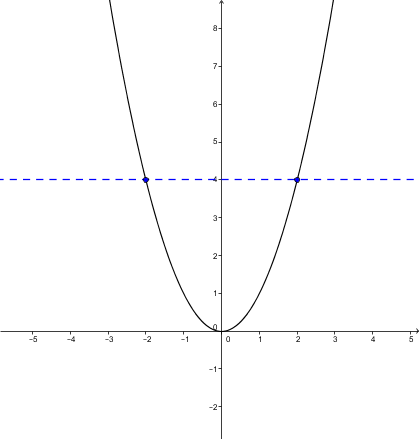
The inverse of this function is not a function.
Since |f^{-1}| is composed of the points obtained by inverting in |f| the variables |x| and |y,| we have |\text{dom}(f^{-1})=\text{ran}(f)| and |\text{ran}(f^{-1})= \text{dom}(f).| Therefore, the domain of |f| becomes the range of |f^{-1}| and vice versa.
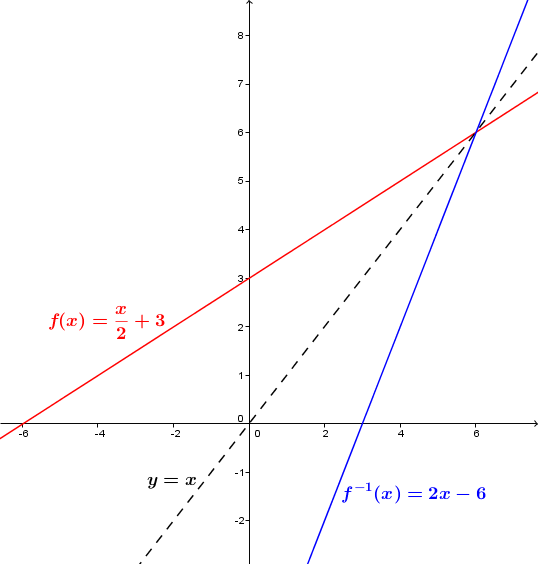
Consider the function |f(x)=\dfrac{x}{2}+3,| which can be written as |y=\dfrac{x}{2}+3.|
The inverse is determined by inverting |x| and |y.|
||y=\dfrac{x}{2}+3\rightarrow x=\dfrac{y}{2}+3||
Isolate |y.|
||x-3=\dfrac{y}{2}\rightarrow 2(x-3)=y\rightarrow 2x-6=y||
Therefore, the inverse is the equation |f^{-1}(x)= 2x-6.|
The following graph represents the function, its inverse, and the axis of reflection.