The Least Common Multiple (LCM) of two or more numbers is the smallest non-zero positive integer that is a multiple of all the numbers.
If you are looking for the least common multiple of some numbers, and one of them is zero, the LCM of these numbers is zero.
There are several ways of finding the LCM of two or more numbers. This concept sheet provides methods for doing so and presents the main types of situations that require you to find the LCM.
The methods presented below only apply to the LCM. To find out how to calculate the LCM and GCF of two or more numbers simultaneously, consult the following concept sheet.
Since we're looking for the least common multiple, we can simply list the multiples of each of the numbers under consideration and identify the smallest common multiple. This simple method is particularly effective with small numbers.
-
List the first multiples of each number.
-
Identify the common multiples.
-
Choose the smallest of the common multiples.
Determine the LCM of |6| and |8.|
-
List the first multiples of each number.
||\begin{align}6&:\left\{6,12,18,24,30,36,...\right\}\\
8&:\left\{8,16,24,32,...\right\}\end{align}|| -
Identify the common multiples.||\begin{align}6&:\{6,12,18,\boldsymbol{\color{#3a9a38}{24}},30,36,\ldots\}\\8&:\{8,16,\boldsymbol{\color{#3a9a38}{24}},32,\ldots\}\end{align}||
-
Choose the smallest of the common multiples.
We see that |\boldsymbol{\color{#3a9a38}{24}}| is the least common multiple.
Answer: |LCM(6,8)=24|
Determine the LCM of |2|, |3| and |4.|
-
List the first multiples of each number.
||\begin{align}2&:\{2,4,6,8,10,12,14,16,18,20,22,24,\ldots\}\\3&:\{3,6,9,12,15,18,21,24,27,30,\ldots\}\\4&:\{4,8,12,16,20,24,28,32,\ldots\}\end{align}|| -
Identify the common multiples. ||\begin{align}2&:\{2,4,6,8,10,\boldsymbol{\color{#3a9a38}{12}},14,16,18,20,22,\boldsymbol{\color{#3a9a38}{24}},\ldots\}\\3&:\{3,6,9,\boldsymbol{\color{#3a9a38}{12}},15,18,21,\boldsymbol{\color{#3a9a38}{24}},27,30,\ldots\}\\4&:\{4,8,\boldsymbol{\color{#3a9a38}{12}},16,20,\boldsymbol{\color{#3a9a38}{24}},28,32,\ldots\}\end{align}||
-
Choose the smallest of the common multiples.
We see that |\boldsymbol{\color{#3a9a38}{12}}| is the least common multiple.
Answer: |LCM(2,3,4)=12|
This method involves finding the LCM of some numbers by simultaneously dividing the numbers by prime factors. The LCM is the product of these prime divisors. Note that this method is slightly different from that used for the GCF. This method is useful when looking for the LCM of two large numbers.
-
Draw a table with Prime factors as the heading of the first column. The headings of the other columns will be the numbers you are interested in.
-
Attempt to divide the numbers in question evenly by prime factors. Start with 2, then 3, 5, 7, and so on. If any of the numbers cannot be evenly divided by the prime factor used, place a hyphen (dash) in the appropriate box. Continue dividing until there is a |1| in each column.
-
Calculate the LCM by multiplying the prime factors in the first column.
Calculate the LCM of |45| and |50.|
-
Draw a table with Prime factors as the heading of the first column. The headings of the other columns will be the numbers you are interested in.
| Prime factors | |45| | |50| |
|---|---|---|
| |\dots| | |\dots| | |\dots| |
-
Attempt to divide the numbers in question evenly by prime factors. Start with 2, then 3, 5, 7, and so on. If any of the numbers cannot be evenly divided by the prime factor used, place a hyphen (dash) in the appropriate box. Continue dividing until there is a |1| in each column.
| Prime Factors | |45| | |50| |
|---|---|---|
| |\color{#3b87cd}{2}| | |-| | |25| |
| |\color{#3b87cd}{3}| | |15| | |-| |
| |\color{#3b87cd}{3}| | |5| | |-| |
| |\color{#3b87cd}{5}| | |1| | |5| |
| |\color{#3b87cd}{5}| | |-| | |1| |
-
Calculate the LCM by multiplying the prime factors in the first column. ||\begin{align}LCM(45,50)&=\boldsymbol{\color{#3b87cd}{2}}\times\boldsymbol{\color{#3b87cd}{3}}\times\boldsymbol{\color{#3b87cd}{3}}\times\boldsymbol{\color{#3b87cd}{5}}\times\boldsymbol{\color{#3b87cd}{5}}\\&=450\end{align}||
This method entails the prime factorization of all the numbers whose LCM is sought. The LCM will be composed of common and non-common factors. This method is very versatile.
-
Decompose each number into a product of prime factors.
-
Identify the prime factors that are common to all numbers, the prime factors that are common to only some numbers and the prime factors that are unique.
-
Write the LCM as a product of all 3 types of prime factors.
Determine the LCM of |27| and |63.|
-
Decompose each number into a product of prime factors.
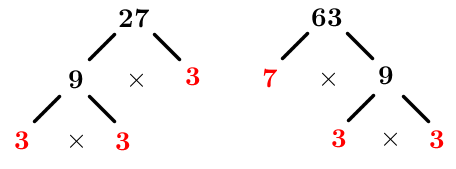
We get this: ||\begin{align}27&=3\times 3\times 3\\ 63&=3\times 3\times 7\end{align}||
-
Identify the prime factors that are common to all numbers, the prime factors that are common to only some numbers and the prime factors that are unique.
Since we're looking for the LCM between two numbers, we only have prime factors that are common to all numbers and unique prime factors.
||\begin{align}27&=\boldsymbol{\color{#333fb1}{3}}\times\boldsymbol{\color{#333fb1}{3}}\times\boldsymbol{\color{#3a9a38}{3}}\\63&=\boldsymbol{\color{#333fb1}{3}}\times\boldsymbol{\color{#333fb1}{3}}\times\boldsymbol{\color{#3a9a38}{7}}\end{align}|| -
Write the LCM as a product of all 3 types of prime factors. ||\begin{align}LCM(27,63)&=\boldsymbol{\color{#333fb1}{3}}\times\boldsymbol{\color{#333fb1}{3}}\times\boldsymbol{\color{#3a9a38}{3}}\times\boldsymbol{\color{#3a9a38}{7}}\\&=189\end{align}||
Determine the LCM of |15,| |55| and |330.|
-
Decompose each number into a product of prime factors.
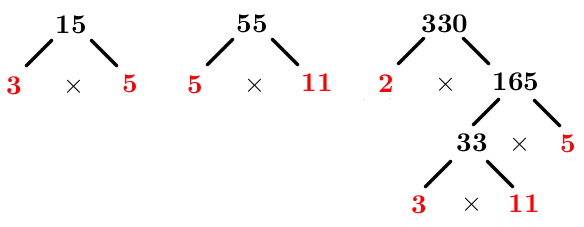
We get this: ||\begin{align}15&=3\times 5\\55&=5\times11\\330&=2\times 3\times 5\times 11\end{align}||
-
Identify the prime factors that are common to all numbers, the prime factors that are common to only some numbers and the prime factors that are unique.
||\begin{align}15&=\boldsymbol{\color{#560fa5}{3}}\times\boldsymbol{\color{#3b87cd}{5}}\\55&=\boldsymbol{\color{#3b87cd}{5}}\times\boldsymbol{\color{#560fa5}{11}}\\330&=\boldsymbol{\color{#3a9a38}{2}}\times\boldsymbol{\color{#560fa5}{3}}\times\boldsymbol{\color{#3b87cd}{5}}\times\boldsymbol{\color{#560fa5}{11}}\end{align}|| -
Write the LCM as a product of all 3 types of prime factors. ||\begin{align}LCM(15,55,330)&=\boldsymbol{\color{#3a9a38}{2}}\times\boldsymbol{\color{#560fa5}{3}}\times\boldsymbol{\color{#3b87cd}{5}}\times\boldsymbol{\color{#560fa5}{11}}\\&=330\end{align}||
In some situations, we may need to use the LCM without being explicitly asked to do so. Here are some examples of situations in which you need to look for the LCM to find the answer.
-
Finding how long it will be before two people meet again, knowing how often they visit a certain place.
-
Finding how long it will take for two events to occur simultaneously again, given the frequency with which the events occur.
-
Finding the smallest square that can be created with rectangles having particular dimensions.
Here's how to successfully solve these situations.
-
Read the problem carefully and decide if you need to find the LCM.
-
Identify the different numbers for which the LCM is sought.
-
Calculate the LCM of these numbers.
-
Interpret the answer.
Two runners circle a track several times. The first takes 30 minutes to complete a lap, while the second takes 45 minutes. If they set off at the same time, after how many minutes will they both be simultaneously back at the starting point?
-
Read the problem carefully and decide if you need to find the LCM.
The question being asked is how long it will take the runners to return to the starting point simultaneously, knowing how often they each pass through it. We'll have to find the LCM. -
Identify the different numbers for which the LCM is sought.
We need to find the least common multiple between |30| and |45.| -
Calculate the LCM of these numbers.
For this step, you can use the method of your choice. Here, we'll use the multiples method.
The 1st runner returns to the starting point after |30,60,\boldsymbol{\color{#3a9a38}{90}},120,\ldots| minutes.
The 2nd runner returns to the starting point after |45,\boldsymbol{\color{#3a9a38}{90}},135,\ldots| minutes.We can see that the |LCM(30,45)=\boldsymbol{\color{#3a9a38}{90}}.|
-
Interpret the answer.
The 2 runners will simultaneously return to the starting point after |90| minutes.