Le Plus Petit Commun Multiple (PPCM) de deux ou plusieurs nombres est le plus petit entier naturel différent de zéro qui est à la fois multiple de tous ces nombres.
Si l'un des nombres dont on cherche le plus petit commun multiple est nul, alors le PPCM de ces nombres est égal à zéro.
Il existe plusieurs façons de déterminer le PPCM entre deux nombres ou plus. Cette fiche proposera des méthodes permettant d'y arriver en plus de présenter les principaux types de mises en situation impliquant la recherche d'un PPCM.
Les méthodes présentées ci-dessous ne concernent que le PPCM. Pour savoir comment calculer le PPCM et le PGCD de deux ou plusieurs nombres simultanément, visite la fiche suivante.
Comme nous cherchons le plus petit commun multiple, on peut simplement dresser la liste des multiples des nombres étudiés et repérer le multiple commun à ces nombres qui est le plus petit. Cette méthode simple convient surtout lorsqu'on a de petits nombres.
-
Dresser une liste des premiers multiples de chacun des nombres.
-
Repérer les multiples communs.
-
Choisir le plus plus petit parmi les multiples communs.
Détermine le PPCM de |6| et |8.|
-
Dresser une liste des premiers multiples de chacun des nombres ||\begin{align}6&:\left\{6,12,18,24,30,36,...\right\}\\
8&:\left\{8,16,24,32,...\right\}\end{align}|| -
Repérer les multiples communs ||\begin{align}6&:\left\{6,12,18,\color{#3a9a38}{24},30,36,...\right\}\\
8&:\left\{8,16,\color{#3a9a38}{24},32,...\right\}\end{align}|| -
Choisir le plus plus petit parmi les multiples communs
On remarque que |\color{#3a9a38}{24}| est le plus petit commun multiple.
Réponse : |PPCM(6,8)=24|
Détermine le PPCM de |2|, |3| et |4.|
- Dresser une liste des premiers multiples de chacun des nombres
||\begin{align}2&:\left\{2,4,6,8,10,12,14,16,18,20,22,24,...\right\}\\3&:\left\{3,6,9,12,15,18,21,24,27,30,...\right\}\\4&:\left\{4,8,12,16,20,24,28,32,...\right\}\end{align}||
- Repérer les multiples communs
||\begin{align}2&:\left\{2,4,6,8,10,\color{#3a9a38}{12},14,16,18,20,22,\color{#3a9a38}{24},...\right\}\\3&:\left\{3,6,9,\color{#3a9a38}{12},15,18,21,\color{#3a9a38}{24},27,30,...\right\}\\4&:\left\{4,8,\color{#3a9a38}{12},16,20,\color{#3a9a38}{24},28,32,...\right\}\end{align}||
- Choisir le plus plus petit parmi les multiples communs
On remarque que |\color{#3a9a38}{12}| est le plus petit commun multiple.
Réponse : |PPCM(2,3,4)=12|
Cette méthode consiste à diviser simultanément les nombres dont on cherche le PPCM par des diviseurs premiers. Le PPCM sera alors le produit de ces diviseurs premiers. Attention, la méthode est légèrement différente de celle présentée pour le PGCD. Cette méthode s'avère pratique lorsque l'on cherche le PPCM entre deux grands nombres.
-
Tracer un tableau dont le titre de la première colonne sera Diviseurs premiers. Les titres des autres colonnes seront les nombres étudiés.
-
Tenter de diviser les nombres étudiés par des diviseurs premiers. On peut commencer par 2, puis par 3, 5, 7 et ainsi de suite. Si un des nombres ne se divise pas par le diviseur premier utilisé, on inscrit un trait dans la case appropriée. On poursuit la division jusqu'à ce qu'on obtienne |1| dans chaque colonne.
-
Calculer le PPCM en multipliant les diviseurs premiers de la première colonne.
Calcule le PPCM de |45| et |50.|
- Tracer un tableau dont le titre de la première colonne sera Diviseurs premiers. Les titres des autres colonnes seront les nombres étudiés.
| Diviseurs premiers | |45| | |50| |
|---|---|---|
| |\dots| | |\dots| | |\dots| |
- Tenter de diviser les nombres étudiés par des diviseurs premiers. On peut commencer par 2, puis par 3, 5, 7 et ainsi de suite. Si un des nombres ne se divise pas par le diviseur premier utilisé, on inscrit un trait dans la case appropriée. On poursuit la division jusqu'à ce qu'on obtienne 1 dans chaque colonne.
| Diviseurs premiers | |45| | |50| |
|---|---|---|
| |\color{#3b87cd}{2}| | |-| | |25| |
| |\color{#3b87cd}{3}| | |15| | |-| |
| |\color{#3b87cd}{3}| | |5| | |-| |
| |\color{#3b87cd}{5}| | |1| | |5| |
| |\color{#3b87cd}{5}| | |-| | |1| |
- Calculer le PPCM en multipliant les diviseurs premiers de la première colonne.
||\begin{align} PPCM(45,50)&=\color{#3b87cd}{2}\times\color{#3b87cd}{3}\times \color{#3b87cd}{3}\times\color{#3b87cd}{5}\times \color{#3b87cd}{5}\\&=450\end{align}||
Cette méthode consiste à faire la factorisation première de tous les nombres dont on cherche le PPCM. Le PPCM sera constitué des facteurs communs et des facteurs qui ne sont pas communs. Cette méthode est très polyvalente.
-
Décomposer chaque nombre en produit de facteurs premiers.
-
Repérer les facteurs premiers communs à tous les nombres, les facteurs premiers qui sont communs à certains nombres seulement et les facteurs premiers qui sont uniques.
-
Écrire le PPCM comme un produit de ces 3 types de facteurs premiers.
Détermine le PPCM de |27| et |63.|
-
Décomposer chaque nombre en produit de facteurs premiers
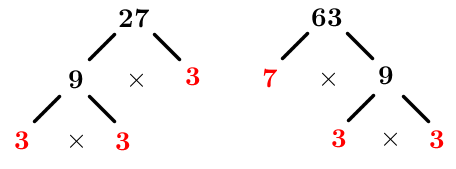
On obtient ceci.||\begin{align}27&=3\times 3\times 3\\ 63&=3\times 3\times 7\end{align}||
-
Repérer les facteurs premiers communs à tous les nombres, les facteurs premiers qui sont communs à certains nombres seulement et les facteurs premiers qui sont uniques
Comme nous cherchons le PPCM entre deux nombres, on aura seulement des facteurs premiers communs à tous les nombres et des facteurs premiers uniques. ||\begin{align}27&=\color{#333fb1}{3}\times \color{#333fb1}{3}\times \color{#3a9a38}{3}\\ 63&=\color{#333fb1}{3}\times \color{#333fb1}{3}\times \color{#3a9a38}{7}\end{align}|| -
Écrire le PPCM comme un produit de ces 3 types de facteurs premiers ||\begin{align}PPCM(27,63)&=\color{#333fb1}{3}\times \color{#333fb1}{3}\times \color{#3a9a38}{3}\times\color{#3a9a38}{7}\\ &=189\end{align}||
Détermine le PPCM entre |15,| |55| et |330.|
- Décomposer chaque nombre en produit de facteurs premiers
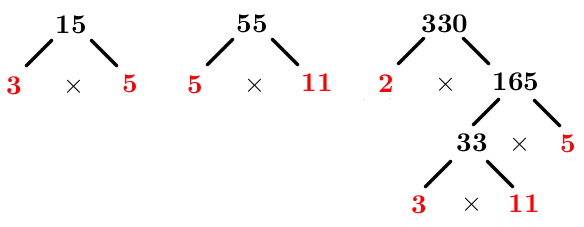
On obtient ceci. ||\begin{align}15&=3\times 5\\55&=5\times11\\330&=2\times 3\times 5\times 11\end{align}||
- Repérer les facteurs premiers communs à tous les nombres, les facteurs premiers qui sont communs à certains nombres seulement et les facteurs premiers qui sont uniques
||\begin{align}15&=\color{#560fa5}{3}\times \color{#3b87cd}{5}\\ 55&=\color{#3b87cd}{5}\times\color{#560fa5}{11}\\ 330&=\color{#3a9a38}{2}\times \color{#560fa5}{3}\times \color{#3b87cd}{5}\times \color{#560fa5}{11}\end{align}|| - Écrire le PPCM comme un produit de ces 3 types de facteurs premiers
||\begin{align}PPCM(15,55,330)&=\color{#3a9a38}{2}\times \color{#560fa5}{3}\times \color{#3b87cd}{5}\times \color{#560fa5}{11}\\ &=330\end{align}||
Dans certaines situations, on devra utiliser le PPCM sans que ce soit demandé explicitement. Voici quelques types de situations où l'on doit chercher le PPCM pour trouver la réponse.
- Trouver dans combien de temps deux individus vont se rencontrer de nouveau sachant à quelle fréquence ils visitent un certain endroit.
- Trouver dans combien de temps deux évènements se produiront simultanément de nouveau sachant la fréquence à laquelle les évènements se produisent.
- Trouver le plus petit carré pouvant être créé avec des rectangles de dimensions données.
Pour résoudre ces situations avec succès, voici comment procéder.
-
Lire attentivement le problème et déceler si on doit utiliser la recherche d'un PPCM.
-
Repérer les différents nombres dont on cherche le PPCM.
-
Calculer le PPCM de ces nombres.
-
Interpréter le résultat.
Deux coureurs font plusieurs fois le tour d'une piste. Le premier prend |30| minutes pour réaliser un tour, alors que le second prend |45| minutes. S'ils sont partis en même temps, après combien de minutes vont-ils se retrouver de nouveau au point de départ simultanément?
-
Lire attentivement le problème et déceler si on doit utiliser la recherche d'un PPCM
Comme nous pouvons le voir, on demande de trouver après combien de temps les coureurs vont se retrouver au point de départ simultanément sachant la fréquence à laquelle il repasse par ce point. On devra utiliser la recherche d'un PPCM. -
Repérer les différents nombres dont on cherche le PPCM
On devra trouver le plus petit commun multiple entre |30| et |45.| -
Calculer le PPCM de ces nombres
Pour cette étape, on peut utiliser la méthode de son choix. Utilisons la méthode des multiples.
Le 1er coureur revient au point de départ après |30,60,\color{#3a9a38}{90},120,...| minutes.
Le 2e coureur revient au point de départ après |45,\color{#3a9a38}{90},135,...| minutes.
On remarque que |PPCM(30,45)=\color{#3a9a38}{90}.| -
Interpréter le résultat
Les 2 coureurs se retrouveront de nouveau au point de départ simultanément après |90| minutes.