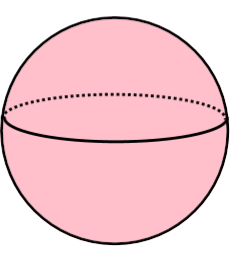
À cause de sa surface entièrement courbe, la sphère est une forme géométrique dont il est impossible de décomposer parfaitement en deux dimensions.
Une sphère est la surface (aire) du lieu des points qui sont situés à une même distance d'un point appelé centre.
Par contre, une boule fait référence à l'espace (volume) occupé par la sphère.
Malgré tout, on peut tenter d'approximer son développement en se basant sur la formule de sa superficie.
Comme expliqué précédemment, il est impossible de décomposer parfaitement une sphère en deux dimensions. Cependant, on peut associer son développement avec celui de plusieurs cercles.

Cette estimation peut être comprise en comparant les formules de l'aire d'un disque et d'une sphère.
||\begin{align} Aire_{disque}&=\pi r^{2}\\
Aire_{sph\grave{e}re}&=4\pi r^{2}\end{align}||
On peut donc remarquer que :
||\begin{align}Aire_{sph\grave{e}re}&=4\times(\pi r^{2})\\
&=4\times Aire_{disque}\end{align}||
d'où l'approximation du développement de la sphère en 4 cercles.
Pour ce faire, on se base sur son allure circulaire pour ensuite y ajouter quelques détails pour dénoter son aspect en trois dimensions.
1. Dessiner un cercle à l'aide d'un compas.

2. Ajouter l'effet de profondeur en dessinant une demi-ellipse pointillée courbée vers l'arrière de la boule.
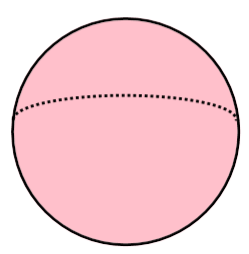
3. Terminer l'effet de profondeur en dessinant la même demi-ellipse, mais courbée vers l'avant et avec un trait plein.