A free-body diagram is a graphic representation of all the forces acting on an object.
A free-body diagram is a simple and effective way of visualizing a problem by representing the forces to be considered. To make a free-body diagram that complies with standards, a few steps need to be followed:
- Determine the object to be analyzed and represent it by a point.
- Represent all forces by vectors whose origin coincides with the object and oriented at the appropriate angles. The size of the arrows should be proportional to the intensity of each force.
- Determine a reference system and position it to simplify problem solving.
- Solve the problem using the component method to find the resultant force.
Once the resultant force has been determined, other information can be deduced from the problem, such as the acceleration of an object using Newton's second law, or the force of friction (if any).
A parachutist launches himself from an airplane. What is the air resistance given that the parachutist has a mass of |\small 70 \: \text {kg}| and falling at constant speed?
First, draw the free-body diagram. The object to be analyzed will be the skydiver.
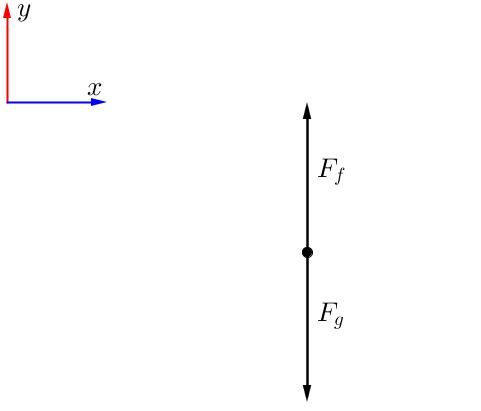
In the free-body diagram, two forces have been represented: the gravitational force (which pulls the skydiver towards the center of the Earth) and the frictional force due to air resistance in the parachute. If the skydiver descends at a constant speed, this means that no acceleration is present during the fall: uniform rectilinear motion (URM) is therefore present. This means that the resultant force is zero: the two forces are of equal magnitude. This is why both arrows have the same dimension.
In this case, the reference system is positioned so that the gravitational force is negative, as it is directed towards the ground (towards the center of the Earth).
To solve the problem mathematically:
||\begin{align} F_{R} = m \times a
\quad \Rightarrow \quad
F_{R} &= m \times 0 \: \text {m/s}^2 \\
F_{R} &= 0 \: \text {N} \\
F_f - F_g &= 0 \: \text {N} \\
F_f &= F_g \\
F_f &= m \times g \\
&= 70 \: \text {kg} \times 9,8 \: \text {N/kg} \\
&= 686 \: \text {N} \end{align}||
Air resistance is therefore |686 \: \text {N}|.
An object is placed on an inclined plane at |\small 15^{\circ}|. What is the acceleration of this object if a friction force of |\small 12 \: \text {N}| ralentit the descent of this |\small 8 \: \text {kg}| ?
Draw the free-body diagram. The object will be represented by a point.
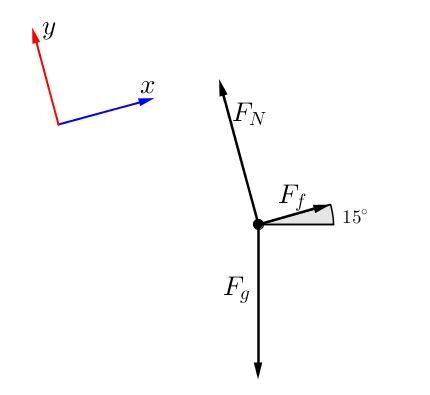
In the free-body diagram, three forces have been represented: the gravitational force (which causes the object to be drawn towards the center of the Earth), the normal force, which is perpendicular to the surface, and the frictional force.
In this case, the reference system is positioned so that the friction force is parallel to the abscissa axis. This also allows the normal force to be placed parallel to the ordinate axis: there is only one force to decompose, namely the gravitational force. This greatly simplifies solving a problem with an inclined plane.
To determine the object's acceleration, only forces parallel to the abscissa axis need be taken into account. The component of the gravitational force parallel to the displacement must therefore be determined.
||\begin{align} F_{R} =F_{f} - F_{g_{x}}
\quad \Rightarrow \quad
F_{R} &= F_{f} - m \times g \times \sin \Theta \\
F_{R} &= 12 \: \text {N} - 8 \: \text {kg} \times 9,8 \: \text {N/kg} \times \sin 15^{\circ} \\
F_{R} &= 12 \: \text {N} - 20,3 \: \text {N} \\
F_{R} &= - 8,3 \: \text {N}\\
m \times a &= - 8,3 \: \text {N}\\
8 \: \text {kg} \times a &= - 8,3 \: \text {N}\\
a&= -1,04 \: \text {N/kg} \end{align}||
Since the value obtained is negative, the object is heading down the inclined plane, with an acceleration of |-1,04 \: \text {N/kg}|.