Un diagramme de corps libre est une représentation graphique de toutes les forces agissant sur un objet.
Un diagramme de corps libre est une façon simple et efficace de visualiser un problème en y représentant les forces à considérer. Pour faire un diagramme de corps libre respectant les normes, quelques étapes doivent être suivies:
- Déterminer l'objet à analyser et le représenter par un point.
- Représenter toutes les forces par des vecteurs dont l'origine coïncide avec l'objet et orientés selon les angles appropriés. La grandeur des flèches devrait être proportionnelle à l'intensité de chacune des forces.
- Déterminer un système de référence et le positionner de manière à simplifier la résolution du problème.
- Résoudre le problème en utilisant la méthode des composantes afin de trouver la force résultante.
Dès que la force résultante est déterminée, d'autres informations peuvent être déduites du problème, comme l'accélération d'un objet grâce à la deuxième loi de Newton ou la force de frottement (si elle existe).
Un parachutiste se lance du haut d'un avion. Quelle est la résistance de l'air sachant que le parachutiste a une masse de |\small 70 \: \text {kg}| et qu'il chute à vitesse constante?
Tout d'abord, il faut dessiner le diagramme de corps libre. L'objet analysé sera le parachutiste.
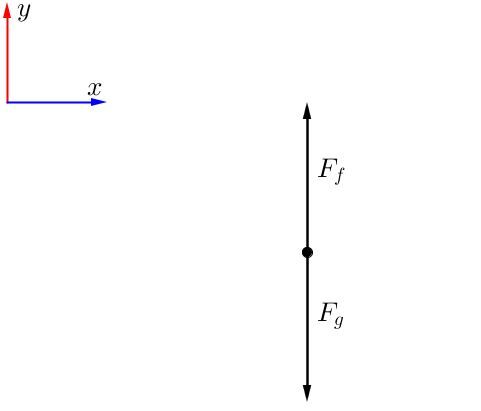
Dans le diagramme de corps libre, deux forces ont été représentées, soit la force gravitationnelle (qui amène le parachutiste vers le centre de la Terre) et la force de frottement due à la résistance de l'air dans le parachute. Si le parachutiste descend à vitesse constante, ceci signifie qu'aucune accélération n'est présente durant la chute: il y a donc présence d'un mouvement rectiligne uniforme (MRU). Ceci signifie que la force résultante est nulle: les deux forces sont de même grandeur. C'est pourquoi les deux flèches ont la même dimension.
Dans ce cas, le système de référence est positionné de façon à ce que la force gravitationnelle soit négative, car elle est orientée vers le sol (vers le centre de la Terre).
Pour résoudre le problème mathématiquement:
||\begin{align} F_{R} = m \times a
\quad \Rightarrow \quad
F_{R} &= m \times 0 \: \text {m/s}^2 \\
F_{R} &= 0 \: \text {N} \\
F_f - F_g &= 0 \: \text {N} \\
F_f &= F_g \\
F_f &= m \times g \\
&= 70 \: \text {kg} \times 9,8 \: \text {N/kg} \\
&= 686 \: \text {N} \end{align}||
La résistance de l'air est donc |686 \: \text {N}|.
Un objet est placé sur un plan incliné à |\small 15^{\circ}|. Quelle est l'accélération de cet objet si une force de frottement de |\small 12 \: \text {N}| ralentit la descente de cet objet de |\small 8 \: \text {kg}| ?
Il faut dessiner le diagramme de corps libre. L'objet sera représenté par un point.
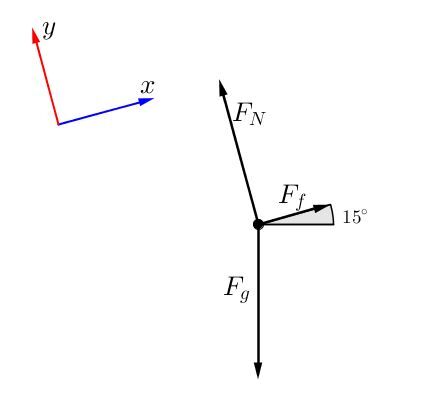
Dans le diagramme de corps libre, trois forces ont été représentées, soit la force gravitationnelle (qui fait en sorte que l'objet est attiré vers le centre de la Terre), la force normale, qui est perpendiculaire à la surface, et la force de frottement.
Dans ce cas, le système de référence est positionné de façon à ce que la force de frottement soit parallèle à l'axe des abscisses. Ceci permet également de placer la force normale parallèle à l'axe des ordonnées: il n'y a qu'une seule force à décomposer, soit la force gravitationnelle. Ceci simplifie beaucoup la résolution d'un problème avec un plan incliné.
Pour déterminer l'accélération de l'objet, il faut tenir compte uniquement des forces parallèles à l'axe des abscisses. Il faudra donc déterminer la composante de la force gravitationnelle parallèle au déplacement.
||\begin{align} F_{R} =F_{f} - F_{g_{x}}
\quad \Rightarrow \quad
F_{R} &= F_{f} - m \times g \times \sin \Theta \\
F_{R} &= 12 \: \text {N} - 8 \: \text {kg} \times 9,8 \: \text {N/kg} \times \sin 15^{\circ} \\
F_{R} &= 12 \: \text {N} - 20,3 \: \text {N} \\
F_{R} &= - 8,3 \: \text {N}\\
m \times a &= - 8,3 \: \text {N}\\
8 \: \text {kg} \times a &= - 8,3 \: \text {N}\\
a&= -1,04 \: \text {N/kg} \end{align}||
Puisque la valeur obtenue est négative, l'objet se dirige vers le bas du plan incliné, avec une accélération de |-1,04 \: \text {N/kg}|.