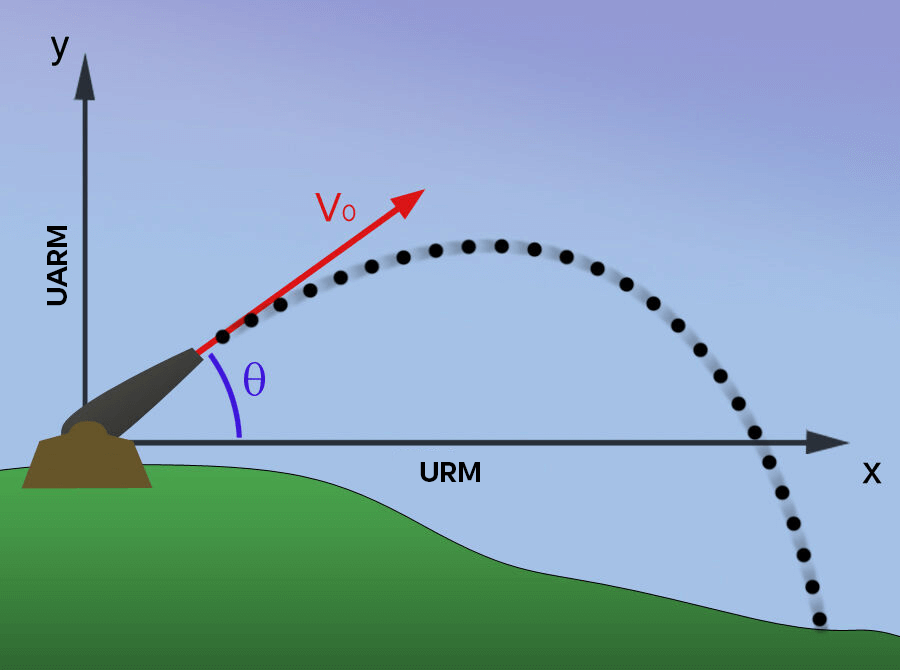
Projectile motion, or ballistic motion, is the motion of an object launched with a velocity that has a horizontal component.
Projectiles are thrown objects that undergo the effect of gravity, meaning that the object moves horizontally and vertically at the same time. A golf ball hit by a player follows the projectile movement: the ball moves horizontally in order to reach the hole, while moving upwards and then downwards due to the action of gravity.
The projectile movement is divided into two parts. The two motions (horizontal and vertical) performed by the projectile are completely independent of each other. Horizontally, the projectile moves at a constant velocity, as in uniform rectilinear motion (URM), whereas vertically, the object moves as a function of gravitational acceleration: it thus acts like a body in free fall. So, whatever the object's horizontal velocity, its vertical motion will vary only as a function of gravitational acceleration (assuming we neglect air resistance).
Another important feature concerns velocity. Initially, velocity must be broken down into its horizontal and vertical components, using trigonometric relations. This is similar to the conversion from polar to Cartesian coordinates when calculating distance and displacement.
Determine the horizontal and vertical velocities of the initial velocity vector below, knowing that its initial velocity is |\small 30,0 \: \text {m/s}| at |\small 30^{\circ}|.
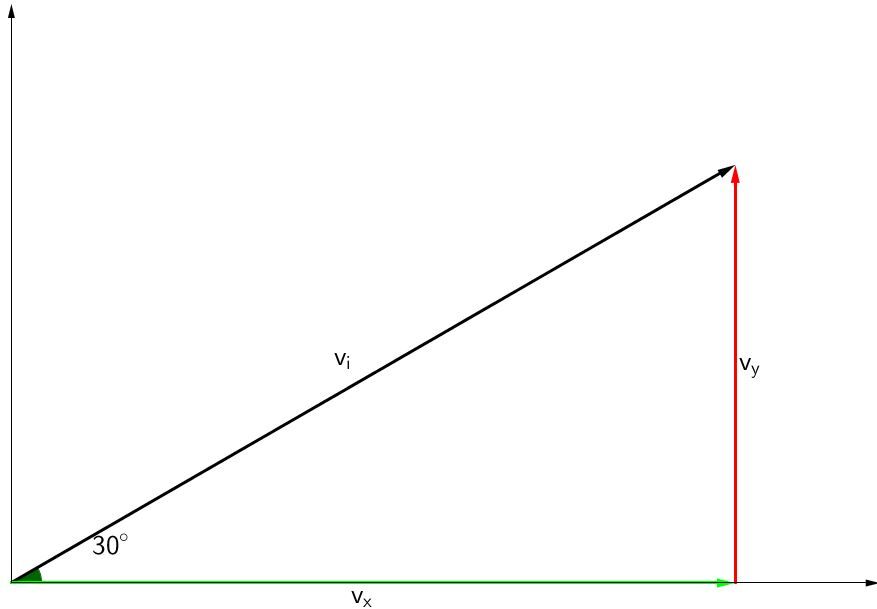
Using trigonometric relations, we can determine the velocity components.
\begin{align}v_{i,x} &= v_{i} \times \cos \theta \quad \Rightarrow \quad v_{i,x} = 30.0 \: \text{m/s} \times \cos 30^{\circ} \nonumber \\&= 26.0 \: \text{m/s}\end{align} \begin{align}v_{i,y} &= v_{i} \times \sin \theta \quad \Rightarrow \quad v_{i,y} = 30.0 \: \text{m/s} \times \sin 30^{\circ} \nonumber \\&= 15.0 \: \text{m/s}\end{align}
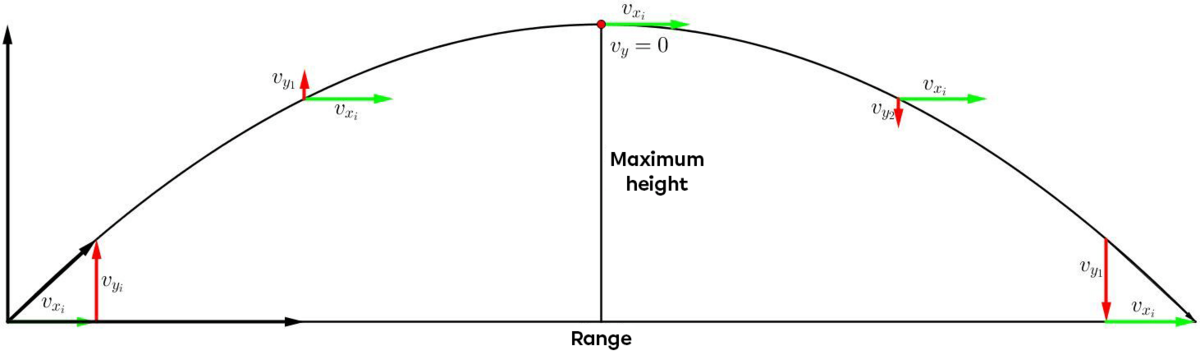
A projectile launched from the ground always falls back to the ground, at the end of its movement, with velocities identical to those it had at the start (assuming that the ground at the end of the movement is neither higher nor lower than the ground at the start), because projectile movement is symmetrical at its mid-point. However, we need to be careful with the signs of vertical motion: at the start, the velocity is positive, because the motion is upward, but at the end, the velocity is negative, because the motion is downward.
Similarly, the time it takes for the projectile to reach the highest point is equal to the time it takes for the same projectile to return to the ground from its maximum height.
When the projectile reaches its maximum height, its vertical velocity is zero. It only has a horizontal velocity, which is constant throughout the projectile's movement, as the horizontal movement is an URM.
In summary, the important characteristics of projectile motion are as follows.
- Horizontal motion is analyzed as URM.
- Vertically, the motion is analyzed as a free-falling object.
- The initial velocity is broken down into its components: the velocity values obtained at the start are the same as those present before the projectile hits the ground.
- Projectile motion is symmetrical: the point of symmetry is at the moment when the projectile reaches its highest point.
- At the highest point, the vertical velocity is zero: the object has only a horizontal velocity component.
There are two types of projectile movement.
An obliquely launched projectile has a horizontal velocity and a vertical velocity.
When the projectile is launched obliquely, it is first necessary to decompose the velocity with which the projectile is launched to determine the horizontal initial velocity and the vertical initial velocity. Subsequently, the problem is solved according to the two distinct motions, i.e. horizontal motion (in URM) and vertical motion (in free fall).
A golfer hits a ball at a velocity of |\small 40,0 \: \text {m/s}| which is propelled at an angle of |\small 15^{\circ}|.
a) How long will it take for the ball to return to the ground?
b) What is the maximum height reached by the ball?
c) What is the horizontal distance (range) covered by the ball?
a) To determine the flight time, first determine the ball's vertical velocity only.
\begin{align}v_{i,y} &= v_{i} \times \sin \theta \quad \Rightarrow \quad v_{i,y} = 40.0 \: \text{m/s} \times \sin 15^{\circ} \nonumber \\&= 10.4 \: \text{m/s}\end{align}
In a projectile movement, the velocity at the beginning of the movement is identical to the velocity at the end of the movement. The known information is therefore as follows.
\begin{align}v_{f,y} &= v_{i,y} + a \cdot \triangle t \quad \Rightarrow \quad \triangle t = \frac {v_{f,y} - v_{i,y}}{a} \\\triangle t &= \frac {(-10.4 \: \text{m/s} - 10.4 \: \text{m/s})}{-9.8 \: \text{m/s}^{2}} \\&\approx 2.1 \: \text{s}\end{align}
The ball will take |2.1 \: \text{s}| before touching the ground again.
b) To determine the maximum height of the ball, it's important to remember that at its highest point, the vertical velocity will be zero. To calculate the height, we need to set the end point at the highest point. In this context, the known variables are as follows.
\begin{align}v_{i,y} &= 10.4 \: \text{m/s} & v_{f,y} &= 0 \: \text{m/s} \\a = g &= -9.8 \: \text{m/s}^2 & \triangle y &= ?\end{align}
In the formula below, |\triangle x| has been replaced by |\triangle y| to reflect the ball's vertical movement.
\begin{align}{v_{f,y}}^2 &= {v_{i,y}}^2 + 2 \cdot g \cdot \triangle y \quad \Rightarrow \quad \nonumber \\triangle y &= \frac{{v_{f,y}}^2 - {v_{i,y}}^2}{2 \cdot g} \nonumber \\ &= \frac{(0 \: \text{m/s})^2 - (10.4 \: \text{m/s})^2}{2 \cdot -9.8 \: \text{m/s}^{2}} \nonumber \\&\approx 5.5 \: \text{m}\end{align} The highest point reached by the ball will be |5.5 \: \text{m}|. It will be reached halfway along the ball's parabolic trajectory.
c) To calculate the distance covered horizontally, or range, we need to determine the projectile's horizontal velocity only.
\begin{align}v_{i,x} &= v_{i} \times \cos \theta \quad \Rightarrow \quad \nonumber \\v_{i,x} &= 40.0 \: \text{m/s} \times \cos 15^{\circ} \nonumber \\&= 38.6 \: \text{m/s} \end{align} Assuming that the time required for horizontal movement is the same as for vertical movement, the information needed to calculate the horizontal distance is given below.
\begin{align} v_{i,x} = v_{f,x} = v_{x} &= 38.6 \: \text{m/s} & \triangle t &= 2.1 \: \text{s} \nonumber \\\triangle x &= ? \end{align}
Since horizontal motion is an URM, only one formula can be used. ||\begin{align}v_{moy} = \frac {\triangle x}{\triangle t} \quad \Rightarrow \quad
\triangle x &= v_{moy} \times \triangle t\\
&= 38.6 \: \text{m/s} \times 2.1 \: \text{s} \\
&\approx 81.1 \: \text{m} \end{align}||
The ball will therefore fall to |81.1 \: \text{m}| from the golfer, then continues its course by rolling on the ground.
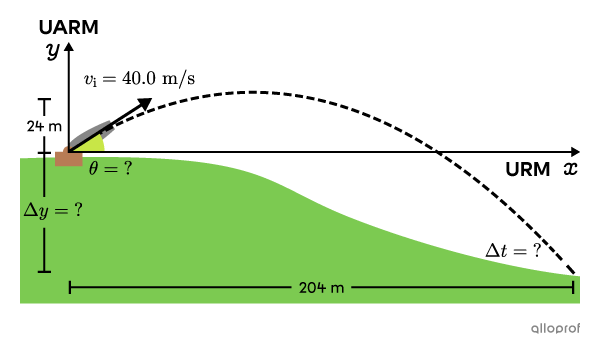
A cannonball is launched obliquely from a hill with a velocity of |40.0\ \text{m/s}.|
The cannonball rises |24\ \text{m}| above the hill then crashes down the hill, |204\ \text{m}| away.
a) What is the barrel tilt angle |(\theta)?|
b) How much time will it take for the cannonball to hit the ground? |(\Delta t)?|
c) What is the height of the hill |(\Delta y)?|
a) Find |\theta|
We can calculate the angle |(\theta)| by analyzing the vertical motion of the cannonball between the launch and the moment it reaches its maximum height.
Using trigonometric relations, we can determine the vertical component of the initial velocity |(v_{\text{i,}y}).|
When the cannonball reaches its maximum height, the vertical component of the final velocity |(v_{\text{f,}y})| is zero.
|\begin{align}
v_{i}&=40.0\ \text{m/s}\\
v_{\text{i,}y}&=v_{\text{i}}\times\sin\theta\\
v_{\text{f,}y}&=0\ \text{m/s}\\
\Delta y&=24\ \text{m (maximum height)}\\
a=g&=-9.8\ \text{m/s}^{2}\\
\theta&=\ ?
\end{align}|
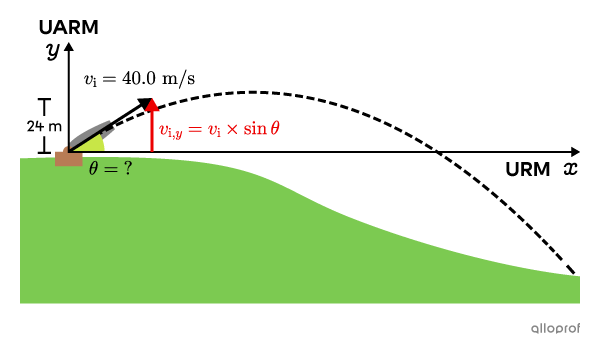
We choose the formula |{v_{\text{f}}}^2={v_{\text{i}}}^2+2\cdot a\cdot \Delta y.|
||{v_{\text{f}}}^2={v_{\text{i}}}^2+2\cdot a\cdot \Delta y\Rightarrow
{v_{\text{f,}y}}^2=(v_{\text{i}}\times \sin \theta)^2+2\cdot a\cdot \Delta y||
We plug in the given values in the formula and isolate |\theta.|
||\begin{align}
(0\ \text{m/s})^2&=(40.0\ \text{m/s}\times\sin\theta)^2+2\cdot -9.8\ \text{m/s}^2\cdot 24\ \text{m}\\
-(2\cdot -9.8\ \text{m/s}^2\cdot 24\ \text{m})&=(40.0\ \text{m/s}\times\sin\theta)^2\\
470.4\ \text{m}^2\text{/s}^2&=(40.0\ \text{m/s}\times\sin\theta)^2\\
\sqrt{470.4\ \text{m}^2\text{/s}^2}&=\sqrt{(40.0\ \text{m/s}\times\sin\theta)^2}\\
21.69\ \text{m/s}&\approx40.0\ \text{m/s}\times\sin\theta\\\\
\dfrac{21.69\ \text{m/s}}{40.0\ \text{m/s}}&\approx\dfrac{40.0\ \text{m/s}\times\sin\theta}{40.0\ \text{m/s}}\\\\
0.5423&\approx\sin\theta\\
32.8^\circ&\approx\theta
\end{align}||
The tilt angle of the barrel is approximately |32.8^\circ.|
b) Find |\Delta t|
We can calculate the time |(\Delta t)| by analyzing the horizontal motion of the cannonball.
With the angle |(\theta)| found from a) and trigonometric relations, we can calculate the horizontal component of the initial velocity |(v_x).|
|\begin{align}
v_{i}&=40.0\ \text{m/s}\\
\theta&=32.8^\circ\\
v_{x}&=v_{\text{i}}\times\cos\theta\\
\Delta x&=204\ \text{m (range)}\\
\Delta t&=\ ?
\end{align}|
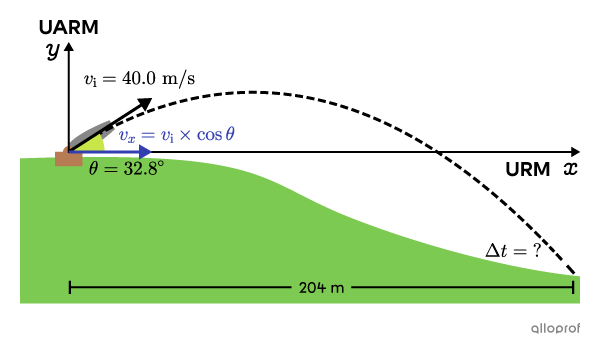
We choose the formula |v=\dfrac{\Delta x}{\Delta t},| we plug in the given values and isolate |\Delta t.|
||\begin{align}v=\dfrac{\Delta x}{\Delta t}\Rightarrow v_x=\dfrac{\Delta x}{\Delta t}\Rightarrow v_{\text{i}}\times\cos\theta&=\dfrac{\Delta x}{\Delta t}\\\\
40.0\ \text{m/s}\times\cos32.8^\circ&=\dfrac{204\ \text{m}}{\Delta t}\\\\
33.6\ \text{m/s}&\approx\dfrac{204\ \text{m}}{\Delta t}\\\\
\Delta t&\approx\dfrac{204\ \text{m}}{33.6\ \text{m/s}}\\\\
\Delta t&\approx6.07\ \text{s}
\end{align}||
The cannonball will take approximately |6.07\ \text{s}| to hit the ground.
c) Find |\Delta y|
With the time |(\Delta t)| found from b) we can deduce the height of the hill by analyzing the vertical movement of the cannonball.
With the angle |(\theta)| found from a) and trigonometric relations, we can calculate the vertical component of the initial velocity |(v_{\text{i,}y}).|
|\begin{align}
\Delta t&=6.07\ \text{s}\\
v_{i}&=40.0\ \text{m/s}\\
\theta&=32.8^\circ\\
v_{\text{i,}y}&=v_{\text{i}}\times\sin\theta\\
a=g&=-9.8\ \text{m/s}^2\\
\Delta y&=\ ?
\end{align}|
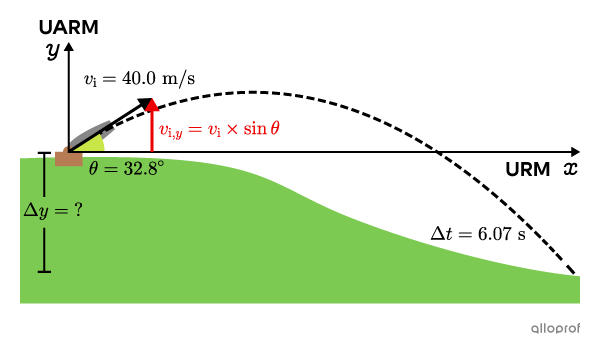
We choose the formula |\Delta y=v_{\text{i,}y}\cdot\Delta t+\dfrac{1}{2}\cdot a\cdot\Delta t^2| and plug in the given values.
||\begin{align}
\Delta y=v_{\text{i,}y}\cdot\Delta t+\dfrac{1}{2}\cdot a\cdot\Delta t^2\Rightarrow\Delta y&=(v_{\text{i}}\times\sin\theta)\times\Delta t+\dfrac{1}{2}\times a\times\Delta t^2\\\\
\Delta y&=(40.0\ \text{m/s}\times\sin32.8^\circ)\times6.07\ \text{s}+\left(\dfrac{1}{2}\times -9.8\ \text{m/s}^2\times(6.07\ \text{s})^2\right)\\\\
\Delta y&\approx-49\ \text{m (under the x-axis)}\
\end{align}||
The height of the hill is approximately |49\ \text{m}.|
A horizontally launched projectile has a horizontal velocity, but no vertical velocity.
In the case of a horizontally-launched projectile, the object starts at the highest point of its movement, then begins its parabolic motion. From a graphical point of view, this movement is similar to a half-parabola.
An archer shoots an arrow horizontally at a velocity of |60{.}0\ \text {m/s}.| He aims at a target located |\small 15 \: \text {m}| from him.
a) How long will it take for the arrow to reach the target?
b) If the arrow is shot from a height of |\small 1.2 \: \text {m}| from the ground, at what height will it hit the target?
c) What will be the arrow's horizontal and vertical velocities after |\small 0.1 \: \text {s}|?
a) To calculate the time needed to reach the target, we can use the horizontal components. The initial velocity is a horizontal velocity only. In addition, the distance between the target and the archer is known.
||\begin{align}v_{i} = v_{f} = v_{x} &= 60.0 \: \text{m/s} &\triangle x &= 15 \: \text{m}\\
\triangle t &= ? \\ \end{align}||
||\begin{align}v_{moy} = \frac {\triangle x}{\triangle t} \quad \Rightarrow \quad
\triangle t &= \frac {\triangle x}{v_{moy}} \\
&= \frac {15 \: \text{m}}{60.0 \: \text{m/s}} \\
&= 0.25 \: \text{s} \end{align}||
b) To calculate the final position of the arrow, work with the vertical components. Remember that in the case of a horizontally launched projectile, the initial velocity is only horizontal: the vertical initial velocity is therefore zero.
||\begin{align}v_{i,y} &= 0 \: \text{m/s} &y_{i} &= 1.2 \: \text{m}\\
a = g &= -9.8 \: \text{m/s}^{2} &\triangle t &= 0.25 \: \text{s} \\ \end{align}||
Using the UARM equations, we find the height at which the arrow will hit the target.
||\begin{align}\triangle y = v_{i,y} \cdot \triangle t + \frac {1}{2} \cdot a \cdot \triangle t^{2} \quad \Rightarrow \quad
\triangle y &= 0 \: \text{m/s} \cdot (0.25 \: \text{s}) + \frac {1}{2} \cdot (-9.8 \: \text{m/s}^2) \cdot (0.25 \: \text{s})^{2}\\
y_f-y_i &= -0.31 \: \text{m}\\
y_{f} - 1.2 \: \text{m} &= -0.31 \: \text{m} \\
y_{f} &= 0.89 \: \text{m}
\end{align}||
The arrow will therefore hit the target at |0.89: \text{m}| from the ground.
c) To determine the vertical velocity, the following information will be useful:
||\begin{align}v_{i,y} &= 0 \: \text{m/s} &v_{f,y} &= \: ?\\
a = g &= -9.8 \: \text{m/s}^{2} &\triangle t &= 0.1 \: \text{s} \\ \end{align}||
Using the free-fall equations, we find the final vertical velocity.
||\begin{align}v_{f,y} = v_{i,y} + a \times \triangle t \quad \Rightarrow \quad
v_{f,y} &= 0 \: \text{m/s} + (-9.8 \: \text{m/s}^{2}) \times (0.1 \: \text{s}) \\
&= -0.98 \: \text{m/s} \end{align}||
As for horizontal velocity, since the projectile is moving in URM, horizontal velocity will always be the same. After |0.1 \: \text{s}|, will therefore be |60 \: \text{m/s}| horizontally and |-0.98 \: \text{m/s}| vertically.