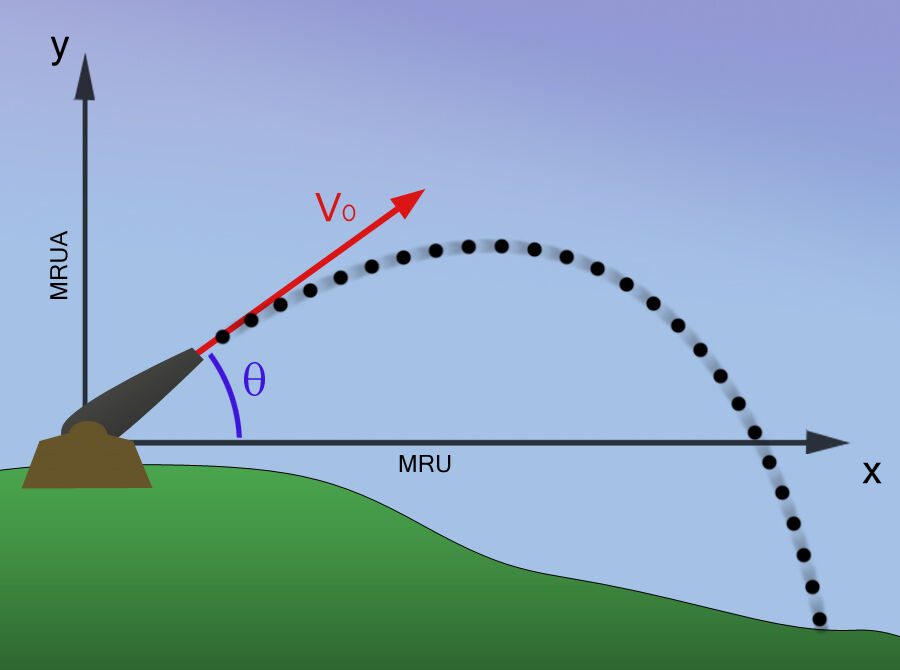
Le mouvement de projectile, ou mouvement de balistique, est le mouvement d'un objet lancé avec une vitesse possédant une composante horizontale.
Les projectiles sont des objets lancés qui subissent l’effet de la gravité, ce qui signifie que l'objet se déplace simultanément à l'horizontale et à la verticale. Une balle de golf frappée par un joueur suit le mouvement de projectile: la balle se déplace à l'horizontale dans le but d'atteindre le trou tout en se déplaçant vers le haut, puis vers le bas en raison de l'action de la gravité.
Le mouvement de projectile se décompose en deux parties. Les deux mouvements (horizontal et vertical) effectués par le projectile sont complètement indépendants l'un de l'autre. À l'horizontale, le projectile se déplace à vitesse constante, comme dans le mouvement rectiligne uniforme (MRU), alors qu'à la verticale, l'objet se déplace en fonction de l'accélération gravitationnelle: il agit donc comme un corps en chute libre. Ainsi, peu importe la vitesse horizontale de l'objet, le mouvement vertical ne variera qu'en fonction de l'accélération gravitationnelle (en supposant qu'on néglige la résistance de l'air).
Une autre caractéristique importante concerne les vitesses. Au départ, la vitesse doit être décomposée en deux composantes, soit une composante horizontale et une composante verticale, en utilisant les relations trigonométriques. Cette conversion est semblable à celle effectuée lorsqu'il faut passer des coordonnées polaires à des coordonnées cartésiennes dans le calcul de la distance parcourue et du déplacement.
Détermine les vitesses horizontale et verticale du vecteur vitesse initiale ci-dessous, sachant que sa vitesse initiale est de |\small 30,0 \: \text {m/s}| à |\small 30^{\circ}|.
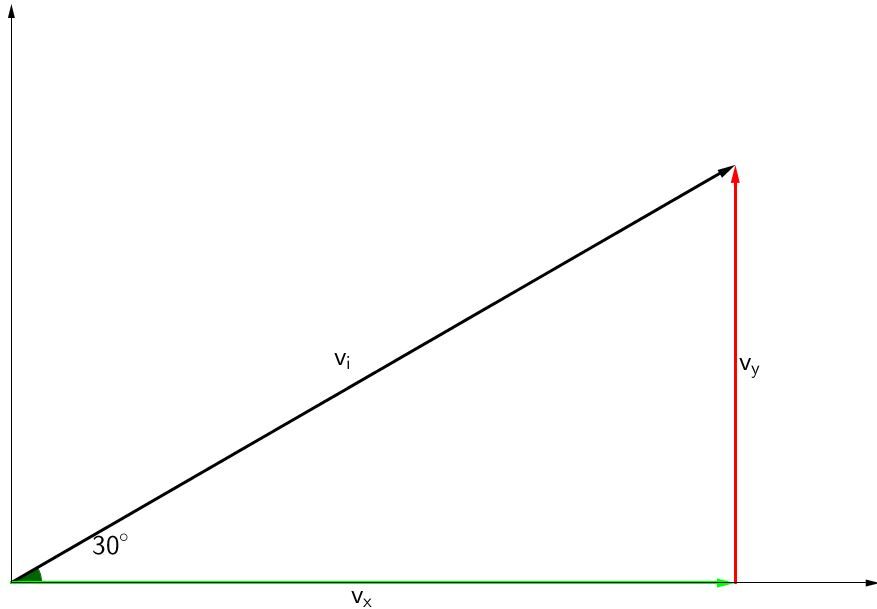
En utilisant les relations trigonométriques, on peut déterminer les composantes de la vitesse.
||\begin{align} v_{i,x} = v_{i} \times \cos \theta \quad \Rightarrow \quad
v_{i,x} &= 30,0 \: \text{m/s} \times \cos 30^{\circ}\\
&= 26,0 \: \text{m/s} \end{align}||
||\begin{align} v_{i,y} = v_{i} \times \sin \theta \quad \Rightarrow \quad
v_{i,y} &= 30,0 \: \text{m/s} \times \sin 30^{\circ}\\
&= 15,0 \: \text{m/s} \end{align}||
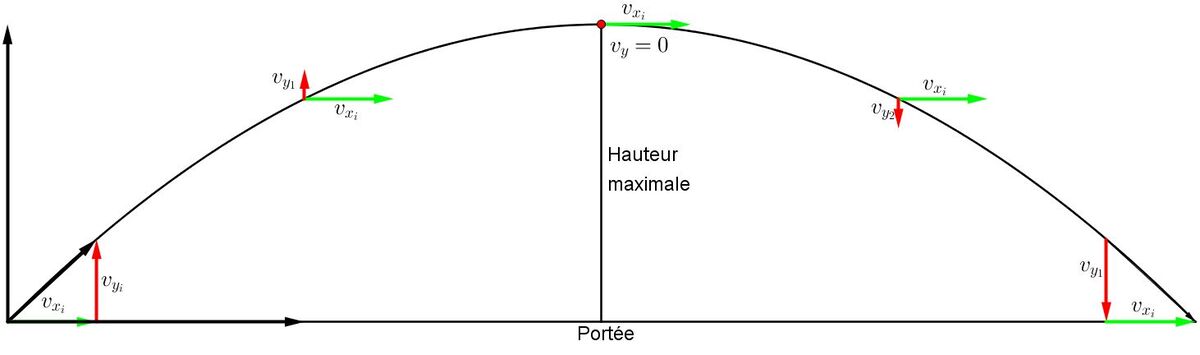
Un projectile lancé du sol retombe toujours au sol, à la fin de son mouvement, avec des vitesses identiques à celles qu'il avait au départ (en assumant que le sol à la fin du mouvement ne soit ni plus haut, ni plus bas que le sol au départ), car le mouvement de projectile est symétrique à son point milieu. Il faut toutefois faire attention aux signes du mouvement vertical: au départ, la vitesse est positive, car le mouvement est orienté vers le haut, mais à la fin, la vitesse est négative, car le mouvement est orienté vers le sol.
Dans le même ordre d'idées, le temps nécessaire pour que le projectile atteigne le point le plus haut est égal au temps nécessaire pour que ce même projectile revienne au sol à partir de la hauteur maximale.
Lorsque le projectile atteint sa hauteur maximale, sa vitesse verticale est nulle. Il possède uniquement une vitesse horizontale qui est constante tout au long du mouvement de projectile, car le mouvement horizontal est un MRU.
En résumé, les caractéristiques importantes du mouvement de projectile sont les suivantes.
- À l'horizontale, on analyse le mouvement comme un MRU.
- À la verticale, on analyse le mouvement comme un objet en chute libre.
- On décompose la vitesse initiale en composantes: les valeurs de vitesses obtenues au départ sont les mêmes que celles présentes avant que le projectile touche le sol.
- Le mouvement de projectile est symétrique: le point de symétrie est situé au moment où le projectile atteint son point le plus haut.
- Au point le plus haut, la vitesse verticale est nulle: l'objet possède uniquement une composante de vitesse horizontale.
Il existe deux types de mouvements de projectiles.
Un projectile lancé obliquement possède une vitesse initiale horizontale et une vitesse initiale verticale.
Lorsque le projectile est lancé obliquement, il faut tout d'abord décomposer la vitesse avec laquelle le projectile est lancé pour déterminer la vitesse initiale horizontale et la vitesse initiale verticale. Par la suite, la résolution du problème se fait selon les deux mouvements distincts, soit le mouvement horizontal (en MRU) et le mouvement vertical (en chute libre).
Un golfeur frappe une balle à une vitesse de |\small 40,0 \: \text {m/s}| qui est propulsée avec un angle de |\small 15^{\circ}|.
a) Combien de temps la balle prendra-t-elle avant de revenir au sol?
b) Quelle est la hauteur maximale atteinte par la balle?
c) Quelle est la distance horizontale (portée) parcourue par la balle?
a) Pour déterminer le temps de vol, il faut tout d'abord déterminer la vitesse uniquement verticale de la balle.
||\begin{align} v_{i,y} = v_{i} \times \sin \theta \quad \Rightarrow \quad
v_{i,y}&= 40,0 \: \text{m/s} \times \sin 15^{\circ}\\
&= 10,4 \: \text{m/s} \end{align}||
Dans un mouvement de projectiles, la vitesse au début du mouvement est identique à la vitesse à la fin du mouvement. Les informations connues sont donc les suivantes.
||\begin{align}v_{i,y} &= 10,4 \: \text{m/s} &v_{f,y} &= -10,4 \: \text{m/s}\\
a = g &= -9,8 \: \text{m/s}^2 &\triangle t &= ? \\ \end{align}||
Il est possible de déterminer, avec ces données, le temps nécessaire pour que la balle revienne au sol.
||\begin{align} v_{f,y} = v_{i,y} + a \cdot \triangle t \quad \Rightarrow \quad
\triangle t &= \frac {v_{f,y} - v_{i,y}}{a}\\
&= \frac {(-10,4 \: \text{m/s} - 10,4 \: \text{m/s})}{-9,8 \: \text{m/s}^{2}} \\
&\approx 2,1 \: \text{s} \end{align}||
La balle prendra |2,1 \: \text{s}| avant de revenir toucher le sol.
b) Pour déterminer la hauteur maximale de la balle, il est important de se rappeler qu'à son point le plus haut, la vitesse verticale sera nulle. Pour calculer la hauteur, il faut fixer le point final au point le plus haut. Dans ce contexte, les variables connues sont les suivantes.
||\begin{align}v_{i,y} &= 10,4 \: \text{m/s} &v_{f,y} &= 0 \: \text{m/s}\\
a = g &= -9,8 \: \text{m/s}^2 &\triangle y &= ? \\ \end{align}||
Dans la formule ci-dessous, |\triangle x| a été remplacé par |\triangle y| afin de refléter le mouvement vertical de la balle.
||\begin{align}{v_{f,y}}^2 = {v_{i,y}}^2 + 2 \cdot g \cdot \triangle y \quad \Rightarrow \quad
\triangle y &= \frac {({v_{f,y}}^2 - {v_{i,y}}^2)}{2 \cdot g}\\
&= \frac {((0 \: \text{m/s})^2 - (10,4 \: \text{m/s})^2)}{2 \cdot -9,8 \: \text{m/s}^{2}} \\
&\approx 5,5 \: \text{m} \end{align}||
Le point le plus haut atteint par la balle sera de |5,5 \: \text{m}|. Il sera atteint à la moitié de la trajectoire parabolique de la balle.
c) Pour calculer la distance parcourue horizontalement, ou portée, il faut déterminer la vitesse uniquement horizontale du projectile.
||\begin{align} v_{i,x} = v_{i} \times \cos \theta \quad \Rightarrow \quad
v_{i,x}&= 40,0 \: \text{m/s} \times \cos 15^{\circ}\\
&= 38,6 \: \text{m/s} \end{align}||
Considérant que le temps nécessaire pour effectuer le mouvement horizontal est le même que celui pour effectuer le mouvement vertical, les informations utiles pour calculer la distance horizontale sont écrites ci-dessous.
||\begin{align}v_{i,x} = v_{f,x} = v_{x} &= 38,6 \: \text{m/s} &\triangle t &= 2,1 \: \text{s}\\
\triangle x &= ? \\ \end{align}||
Puisque le mouvement horizontal est un MRU, une seule formule peut être utilisée.
||\begin{align}v_{moy} = \frac {\triangle x}{\triangle t} \quad \Rightarrow \quad
\triangle x &= v_{moy} \times \triangle t\\
&= 38,6 \: \text{m/s} \times 2,1 \: \text{s} \\
&\approx 81,1 \: \text{m} \end{align}||
La balle tombera donc à |81,1 \: \text{m}| du golfeur, puis continuera sa course en roulant sur le sol.
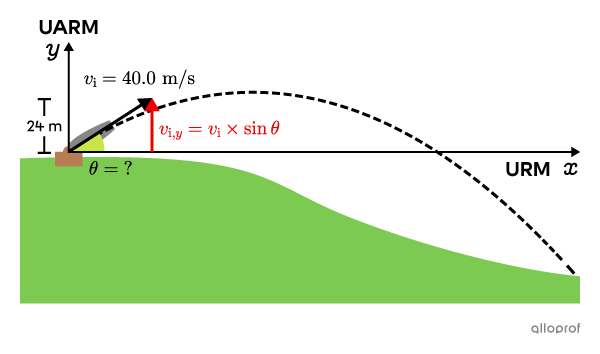
Un boulet de canon est lancé obliquement à partir d’une colline avec une vitesse de |40{,}0\ \text{m/s}.|
Le boulet monte de |24\ \text{m}| au-dessus de la colline et s’écrase en bas de la colline, |204\ \text{m}| plus loin.
a) Quel est l’angle d’inclinaison du canon |(\theta)?|
b) Combien de temps le boulet mettra-t-il avant de s’écraser au sol |(\Delta t)?|
c) Quelle est la hauteur de la colline |(\Delta y)?|
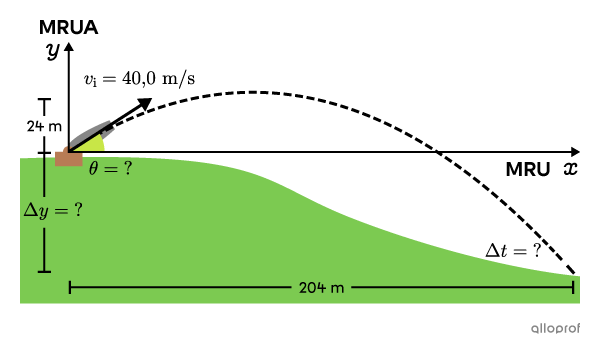
a) Trouver |\theta|
On peut calculer l’angle |(\theta)| en analysant le mouvement vertical du boulet entre son lancement et le moment où il atteint sa hauteur maximale.
En utilisant les relations trigonométriques, on peut déterminer la composante verticale de la vitesse initiale |(v_{\text{i,}y}).|
Lorsque le boulet atteint sa hauteur maximale, la composante verticale de la vitesse finale |(v_{\text{f,}y})| est nulle.
|\begin{align}
v_{i}&=40{,}0\ \text{m/s}\\
v_{\text{i,}y}&=v_{\text{i}}\times\sin\theta\\
v_{\text{f,}y}&=0\ \text{m/s}\\
\Delta y&=24\ \text{m (hauteur maximale)}\\
a=g&=-9{,}8\ \text{m/s}^{2}\\
\theta&=\ ?
\end{align}|
On choisit la formule |{v_{\text{f}}}^2={v_{\text{i}}}^2+2\cdot a\cdot \Delta y.|
||{v_{\text{f}}}^2={v_{\text{i}}}^2+2\cdot a\cdot \Delta y\Rightarrow
{v_{\text{f,}y}}^2=(v_{\text{i}}\times \sin \theta)^2+2\cdot a\cdot \Delta y||
On remplace les variables dans la formule et on isole |\theta.|
||\begin{align}
(0\ \text{m/s})^2&=(40{,}0\ \text{m/s}\times\sin\theta)^2+2\cdot -9{,}8\ \text{m/s}^2\cdot 24\ \text{m}\\
-(2\cdot -9{,}8\ \text{m/s}^2\cdot 24\ \text{m})&=(40{,}0\ \text{m/s}\times\sin\theta)^2\\
470{,}4\ \text{m}^2\text{/s}^2&=(40{,}0\ \text{m/s}\times\sin\theta)^2\\
\sqrt{470{,}4\ \text{m}^2\text{/s}^2}&=\sqrt{(40{,}0\ \text{m/s}\times\sin\theta)^2}\\
21{,}69\ \text{m/s}&\approx40{,}0\ \text{m/s}\times\sin\theta\\\\
\dfrac{21{,}69\ \text{m/s}}{40{,}0\ \text{m/s}}&\approx\dfrac{40{,}0\ \text{m/s}\times\sin\theta}{40{,}0\ \text{m/s}}\\\\
0{,}5423&\approx\sin\theta\\
32{,}8^\circ&\approx\theta
\end{align}||
L’angle d'inclinaison du canon est d’environ |32{,}8^\circ.|
b) Trouver |\Delta t|
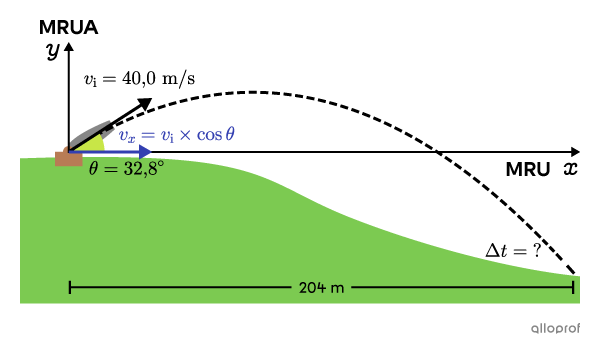
On peut calculer le temps |(\Delta t)| en analysant le mouvement horizontal du boulet.
En utilisant l’angle |(\theta)| trouver en a) et les relations trigonométriques, on peut déterminer la composante horizontale de la vitesse initiale |(v_x).|
|\begin{align}
v_{i}&=40{,}0\ \text{m/s}\\
\theta&=32{,}8^\circ\\
v_{x}&=v_{\text{i}}\times\cos\theta\\
\Delta x&=204\ \text{m (portée)}\\
\Delta t&=\ ?
\end{align}|
On choisit la formule |v=\dfrac{\Delta x}{\Delta t},| on remplace les variables et on isole |\Delta t.|
||\begin{align}v=\dfrac{\Delta x}{\Delta t}\Rightarrow v_x=\dfrac{\Delta x}{\Delta t}\Rightarrow v_{\text{i}}\times\cos\theta&=\dfrac{\Delta x}{\Delta t}\\\\
40{,}0\ \text{m/s}\times\cos32{,}8^\circ&=\dfrac{204\ \text{m}}{\Delta t}\\\\
33{,}6\ \text{m/s}&\approx\dfrac{204\ \text{m}}{\Delta t}\\\\
\Delta t&\approx\dfrac{204\ \text{m}}{33{,}6\ \text{m/s}}\\\\
\Delta t&\approx6{,}07\ \text{s}
\end{align}||
Le boulet mettra environ |6{,}07\ \text{s}| avant de s’écraser au sol.
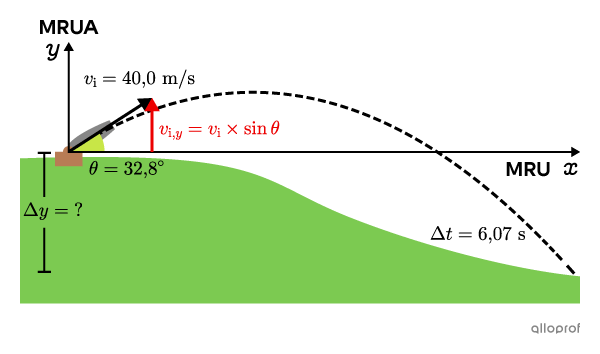
c) Trouver |\Delta y|
En utilisant le temps |(\Delta t)| trouvé en b), on peut déduire la hauteur de la colline en analysant le mouvement vertical du boulet.
En utilisant l’angle |(\theta)| trouvé en a) et les relations trigonométriques, on peut déterminer la composante verticale de la vitesse initiale |(v_{\text{i,}y}).|
|\begin{align}
\Delta t&=6{,}07\ \text{s}\\
v_{i}&=40{,}0\ \text{m/s}\\
\theta&=32{,}8^\circ\\
v_{\text{i,}y}&=v_{\text{i}}\times\sin\theta\\
a=g&=-9{,}8\ \text{m/s}^2\\
\Delta y&=\ ?
\end{align}|
On choisit la formule |\Delta y=v_{\text{i,}y}\cdot\Delta t+\dfrac{1}{2}\cdot a\cdot\Delta t^2| et on remplace les variables.
||\begin{align}
\Delta y=v_{\text{i,}y}\cdot\Delta t+\dfrac{1}{2}\cdot a\cdot\Delta t^2\Rightarrow\Delta y&=(v_{\text{i}}\times\sin\theta)\times\Delta t+\dfrac{1}{2}\times a\times\Delta t^2\\\\
\Delta y&=(40{,}0\ \text{m/s}\times\sin32{,}8^\circ)\times6{,}07\ \text{s}+\left(\dfrac{1}{2}\times -9{,}8\ \text{m/s}^2\times(6{,}07\ \text{s})^2\right)\\\\
\Delta y&\approx-49\ \text{m (sous l'axe des}\ x)
\end{align}||
La hauteur de la colline est d’environ |49\ \text{m}.|
Un projectile lancé horizontalement possède une vitesse initiale horizontale, mais ne possède aucune vitesse initiale verticale.
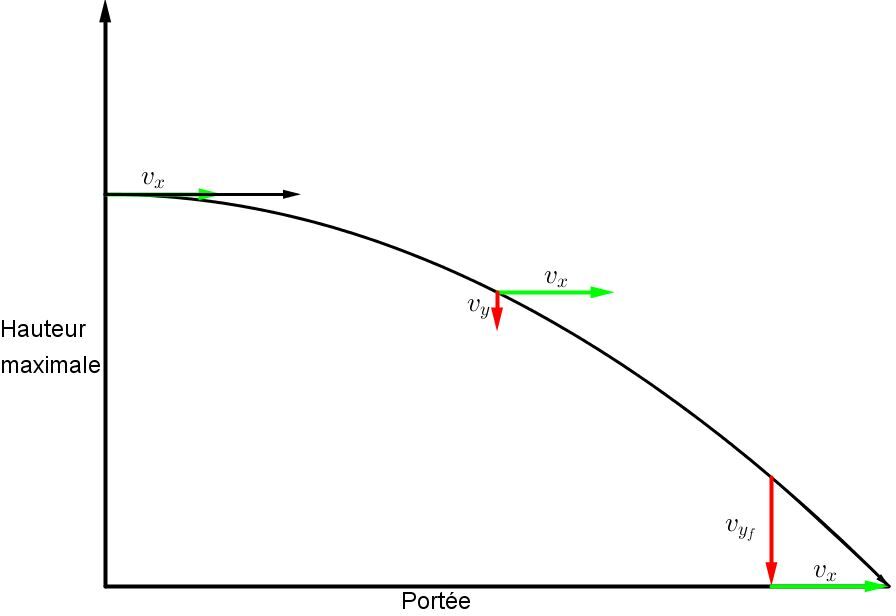
Dans le cas d'un projectile lancé horizontalement, l'objet débute au point le plus haut de son mouvement, puis entreprend son mouvement parabolique. D'un point de vue graphique, ce mouvement est semblable à une demi-parabole.
Un archer tire une flèche horizontalement à une vitesse de |\small 60,0 \: \text {m/s}|. Il vise une cible située à |\small 15 \: \text {m}| de lui.
a) Combien de temps la flèche prendra-t-elle pour atteindre la cible?
b) Si la flèche est tirée d’une hauteur de |\small 1,2 \: \text {m}| du sol, à quelle hauteur frappera-t-elle la cible ?
c) Quelles seront les vitesses horizontale et verticale de la flèche après |\small 0,1 \: \text {s}|?
a) Pour calculer le temps nécessaire pour atteindre la cible, il est possible d'utiliser les composantes horizontales. La vitesse initiale est une vitesse uniquement horizontale. De plus, la distance entre la cible et l'archer est connue.
||\begin{align}v_{i} = v_{f} = v_{x} &= 60,0 \: \text{m/s} &\triangle x &= 15 \: \text{m}\\
\triangle t &= ? \\ \end{align}||
||\begin{align}v_{moy} = \frac {\triangle x}{\triangle t} \quad \Rightarrow \quad
\triangle t &= \frac {\triangle x}{v_{moy}} \\
&= \frac {15 \: \text{m}}{60 \: \text{m/s}} \\
&= 0,25 \: \text{s} \end{align}||
b) Pour calculer la position finale de la flèche, il faut travailler avec les composantes verticales. Il faut se rappeler que dans le cas d'un projectile lancé horizontalement, la vitesse initiale est uniquement horizontale: la vitesse initiale verticale est donc nulle.
||\begin{align}v_{i,y} &= 0 \: \text{m/s} &y_{i} &= 1,2 \: \text{m}\\
a = g &= -9,8 \: \text{m/s}^{2} &\triangle t &= 0,25 \: \text{s} \\ \end{align}||
En utilisant les équations du MRUA, on trouve la hauteur à laquelle la flèche atteindra la cible.
||\begin{align}\triangle y = v_{i,y} \cdot \triangle t + \frac {1}{2} \cdot a \cdot \triangle t^{2} \quad \Rightarrow \quad
\triangle y &= 0 \: \text{m/s} \cdot (0,25 \: \text{s}) + \frac {1}{2} \cdot (-9,8 \: \text{m/s}^2) \cdot (0,25 \: \text{s})^{2}\\
y_f-y_i &= -0,31 \: \text{m}\\
y_{f} - 1,2 \: \text{m} &= -0,31 \: \text{m} \\
y_{f} &= 0,89 \: \text{m}
\end{align}||
La flèche touchera donc la cible à |0,89 \: \text{m}| du sol.
c) Pour déterminer la vitesse verticale, les informations suivantes seront utiles:
||\begin{align}v_{i,y} &= 0 \: \text{m/s} &v_{f,y} &= \: ?\\
a = g &= -9,8 \: \text{m/s}^{2} &\triangle t &= 0,1 \: \text{s} \\ \end{align}||
En utilisant les équations de la chute libre, on trouve la vitesse finale verticale.
||\begin{align}v_{f,y} = v_{i,y} + a \times \triangle t \quad \Rightarrow \quad
v_{f,y} &= 0 \: \text{m/s} + (-9,8 \: \text{m/s}^{2}) \times (0,1 \: \text{s}) \\
&= -0,98 \: \text{m/s} \end{align}||
Quant à la vitesse horizontale, puisque le projectile se déplace en MRU, la vitesse horizontale sera toujours la même. Les vitesses, après |0,1 \: \text{s}|, seront donc de |60 \: \text{m/s}| à l'horizontale et |-0,98 \: \text{m/s}| à la verticale.