A vector placed on a Cartesian plane can be defined by the horizontal (|x|) and vertical (|y|) displacement between its origin and end point. These displacements, called components, allow the vector’s magnitude (norm) and direction to be calculated. Also, we can find a vector’s components from its magnitude and direction.
When a vector is represented on a Cartesian plane, a right triangle can be formed where the hypotenuse corresponds to the vector and the triangle’s legs correspond to its |x| and |y| components.
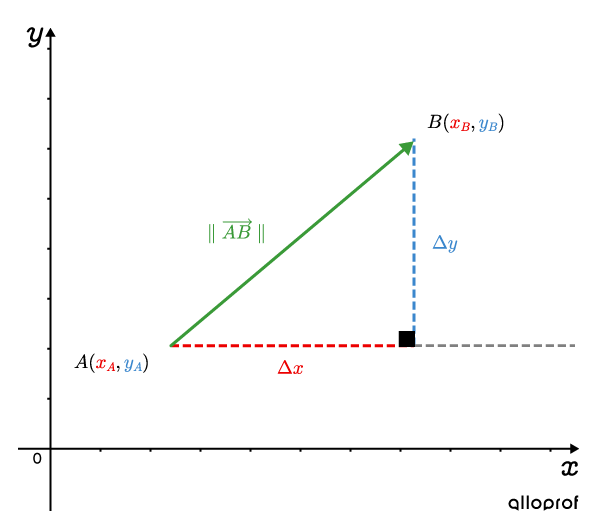
Consider 2 points in the Cartesian plane, |A(x_{\small{A}},y_{\small{A}})| and |B(x_{\small{B}},y_{\small{B}}).| Define the vector |\overrightarrow{AB}| as follows:
||\begin{align}\overrightarrow{AB}&=(\color{#EC0000}{\Delta x},\color{#3B87CD}{\Delta y})\\&=(\color{#EC0000}{x_{\small{B}}-x_{\small{A}}},\color{#3B87CD}{y_{\small{B}}-y_{\small{A}}})\\&=(\color{#EC0000}{a},\color{#3B87CD}{b})\end{align}||
The following interactive animation makes it easier to visualize the vector’s components as the legs of a right triangle.
What are the components |\color{#EC0000}{a}| and |\color{#3B87CD}{b}| of vector |\overrightarrow{AB}|?
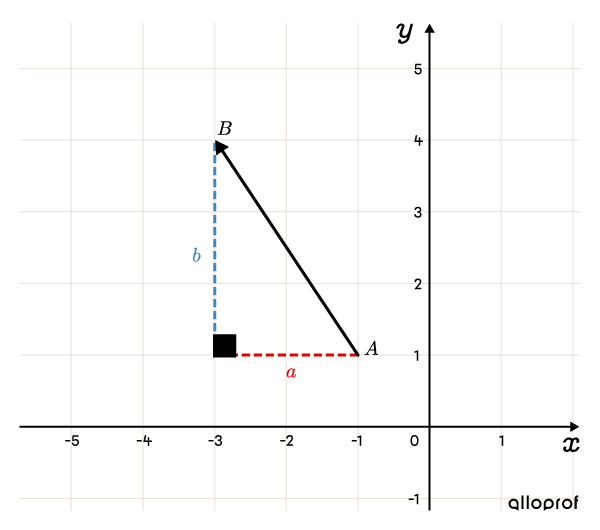
The coordinates of point |A,| corresponding to the vector’s origin are |( -1,1).| Point |B,| corresponds to the vector’s end point and its coordinates are |(-3,4).| To calculate the horizontal component |\color{#EC0000}{a},| we have:
||\begin{align}\color{#EC0000}{a}&=\Delta x\\&=x_{\small{B}}-x_{\small{A}}\\&=-3--1\\&=\color{#EC0000}{-2}\end{align}||
For the vertical component |\color{#3B87CD}{b},| we have:
||\begin{align}\color{#3B87CD}{b}&=\Delta y\\&=y_{\small{B}}-y_{\small{A}}\\&=4-1\\&=\color{#3B87CD}{3}\end{align}||
Therefore, the components of vector |\overrightarrow{AB}| are |(\color{#EC0000}{-2},\color{#3B87CD}{3}).|
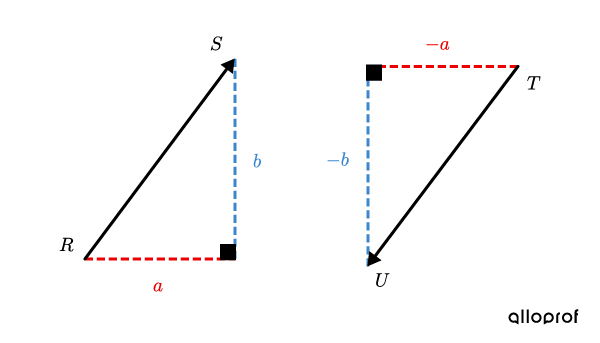
Consider |\overrightarrow{RS}| and |\overrightarrow{TU},| two opposite vectors that are parallel and have the same magnitude (norm), but point in the opposite direction.
If the components of |\overrightarrow{RS}| are |(\color{#EC0000}{a},\color{#3B87CD}{b}),| then the components of |\overrightarrow{TU}| must be |\overrightarrow{RS}||(\color{#EC0000}{-a},\color{#3B87CD}{-b}).|
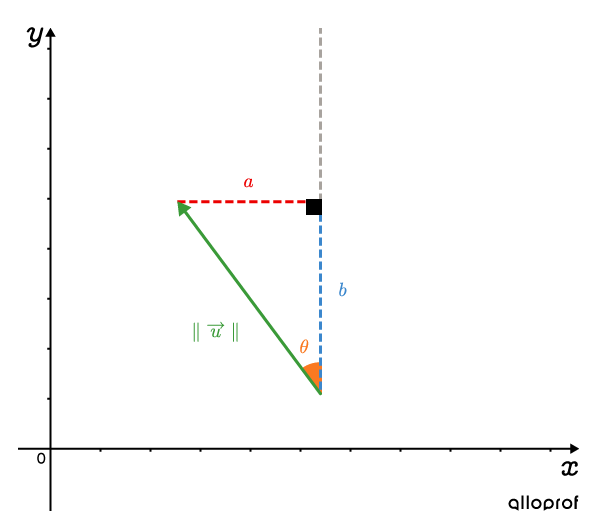
Consider vector |\overrightarrow{u}|. Using trigonometric ratios in a right triangle, the relationship between the vector’s components |\color{#EC0000}{a}| and |\color{#3B97CD}{b},| the magnitude (norm) |\color{#3A9A38}{{\parallel}\overrightarrow{u}{\parallel}},| and direction |\color{#FA7921}{\theta}| can be found.
||\begin{align}\cos\color{#FA7921}{\theta}&=\dfrac{\color{#EC0000}{a}}{\color{#3A9A38}{{\parallel}\overrightarrow{u}{\parallel}}}\\\\\sin\color{#FA7921}{\theta}&=\dfrac{\color{#3B87CD}{b}}{\color{#3A9A38}{{\parallel}\overrightarrow{u}{\parallel}}}\\\\\tan\color{#FA7921}{\theta}&=\dfrac{\color{#3B87CD}{b}}{\color{#EC0000}{a}}\end{align}||

The trigonometric relations are valid only if angle |\color{#FA7921}{\theta}| is defined with respect to a horizontal axis.
For vector |\overrightarrow{u}| where the angle |\color{#FA7921}{\theta}| is defined with respect to a vertical axis (as shown in the image), the following trigonometric relations are obtained instead.
||\begin{align}\cos\color{#FA7921}{\theta}&=\dfrac{\color{#3B87CD}{b}}{\color{#3A9A38}{{\parallel}\overrightarrow{u}{\parallel}}}\\\\\sin\color{#FA7921}{\theta}&=\dfrac{\color{#EC0000}{a}}{\color{#3A9A38}{{\parallel}\overrightarrow{u}{\parallel}}}\\\\\tan\color{#FA7921}{\theta}&=\dfrac{\color{#EC0000}{a}}{\color{#3B87CD}{b}}\end{align}||
Calculating a vector’s components involves one of the following situations:
When the magnitude (norm) and one component of a vector are known, the other component can be calculated using the Pythagorean theorem.
What is the vertical component |\color{#3B87CD}{b}| of vector |\overrightarrow{u}|, if the horizontal component is |\color{#EC0000}{a}=\color{#EC0000}{-8.4}| and the magnitude is |\color{#3A9A38}{{\parallel}\overrightarrow{u}{\parallel}}=\color{#3A9A38}{14}|?
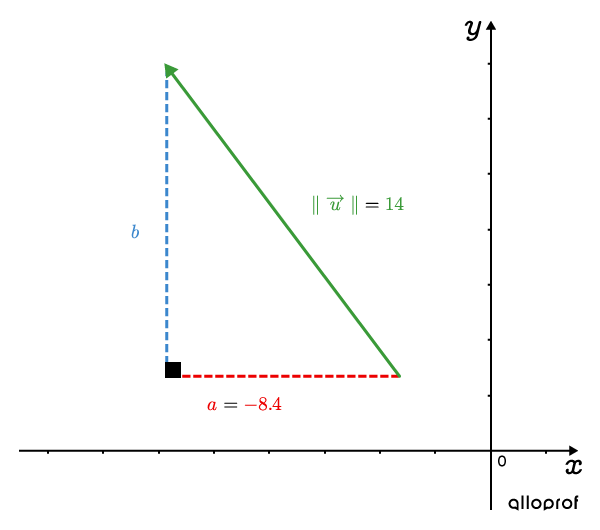
From the right triangle formed by vector |\overrightarrow{u},| the Pythagorean Theorem can be applied.
||\begin{align}\color{#EC0000}{a}^2+\color{#3B87CD}{b}^2&=\color{#3A9A38}{{\parallel}\overrightarrow{u}{\parallel}}^2\\(\color{#EC0000}{-8.4})^2+\color{#3B87CD}{b}^2&=\color{#3A9A38}{14}^2\\70.56+\color{#3B87CD}{b}^2&=196\\\color{#3B87CD}{b}^2&=125.44\\\color{#3B87CD}{b}&=\pm11.2\end{align}||
The answer |-11.2| is rejected because the vertical displacement of vector |\overrightarrow{u}| points in the positive direction of the |y|-axis. Therefore, the vertical component of vector |\overrightarrow{u}| is |\color{#3B87CD}{b}=\color{#3B87CD}{11.2}.|
When the direction and one component of a vector are known, the other component can be calculated using the tangent ratio.
Consider vector |\overrightarrow{u}=(\color{#EC0000}{a},\color{#3B87CD}{b})| where the direction |\color{#FA7921}{\theta}| and one component are known. From the trigonometric relations in a vector, we have:
||\tan\color{#FA7921}{\theta}=\dfrac{\color{#3B87CD}{b}}{\color{#EC0000}{a}}||
The following formulas are obtained by isolating |\color{#EC0000}{a}| and |\color{#3B87CD}{b}.|
||\begin{align}\color{#EC0000}{a}&=\dfrac{\color{#3B87CD}{b}}{\tan\color{#FA7921}{\theta}}\\\\\color{#3B87CD}{b}&=\color{#EC0000}{a}\tan\color{#FA7921}{\theta}\end{align}||
What is the horizontal component |\color{#EC0000}{a}| of vector |\overrightarrow{u},| where the vertical component is |\color{#3B87CD}{b}=\color{#3B87CD}{4.45}| and the direction is |\color{#FA7921}{\theta}=\color{#FA7921}{51^\circ}|?
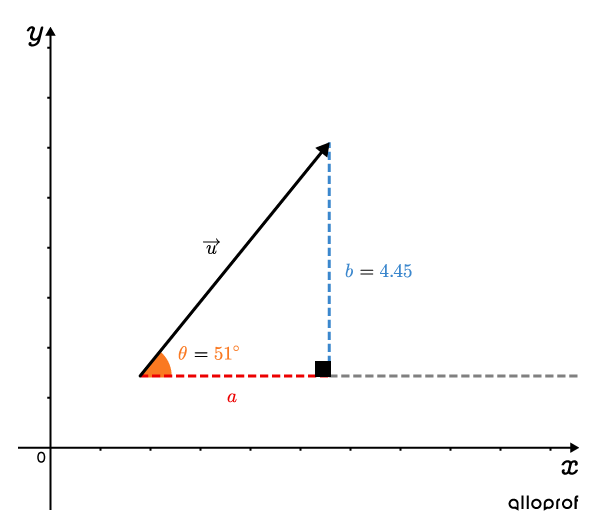
From the right triangle formed by vector |\overrightarrow{u},| the formula can be used to calculate the horizontal component |\color{#EC0000}{a}.|
||\begin{align}\color{#EC0000}{a}&=\dfrac{\color{#3B87CD}{ b}}{\tan\color{#FA7921}{\theta}}\\\\&=\dfrac{\color{#3B87CD}{4.45}}{\tan\color{#FA7921}{51^\circ}}\\\\\color{#EC0000}{a}&\approx\color{#EC0000}{3.6}\end{align}||
Therefore, the horizontal component of vector |\overrightarrow{u}| is |\color{#EC0000}{3.6}.|
When the direction and magnitude (norm) of a vector are given, its components can be calculated using trigonometric ratios.
Consider vector |\overrightarrow{u}=(\color{#EC0000}{a},\color{#3B87CD}{b})|, where the magnitude |\color{#3A9A38}{{\parallel}\overrightarrow{u}{\parallel}}| and direction |\color{#FA7921}{\theta}| are known. From the trigonometric relations in a vector, the following is given:
||\begin{align}\cos\color{#FA7921}{\theta}&=\dfrac{\color{#EC0000}{a}}{\color{#3A9A38}{{\parallel}\overrightarrow{u}{\parallel}}}\\\\\sin\color{#FA7921}{\theta}&=\dfrac{\color{#3B87CD}{b}}{\color{#3A9A38}{{\parallel}\overrightarrow{u}{\parallel}}}\end{align}||
The following formulas are obtained by isolating |\color{#EC0000}{a}| and |\color{#3B87CD}{b}.|
||\begin{align}\color{#EC0000}{a}&=\color{#3A9A38}{{\parallel}\overrightarrow{u}{\parallel}}\cos\color{#FA7921}{\theta}\\\\\color{#3B87CD}{b}&=\color{#3A9A38}{{\parallel}\overrightarrow{u}{\parallel}}\sin\color{#FA7921}{\theta}\end{align}||
What are the components of vector |\overrightarrow{u}|, if the magnitude (norm) is |\color{#3A9A38}{{\parallel}\overrightarrow{u}{\parallel}}=\color{#3A9A38}{5.8}| and direction is |\color{#FA7921}{\theta}=\color{#FA7921}{320^\circ}|?
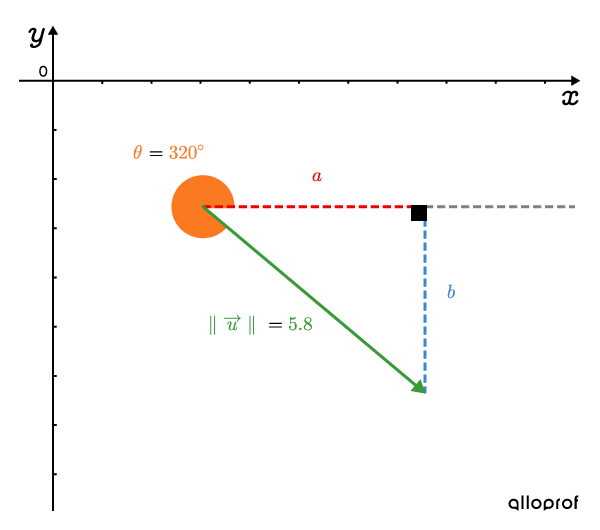
From the right triangle formed by vector |\overrightarrow{u},| the formula can be used to calculate the horizontal component |\color{#EC0000}{a}.|
||\begin{align}\color{#EC0000}{a}&=\color{#3A9A38}{{\parallel}\overrightarrow{u}{\parallel}}\cos\color{#FA7921}{\theta}\\\color{#EC0000}{a}&=\color{#3A9A38}{5.8}\cos\color{#FA7921}{320^\circ}\\ \color{#EC0000}{a}&\approx\color{#EC0000}{4.44}\end{align}||
For the vertical component |\color{#3B87CD}{b},| we have:
||\begin{align}\color{#3B87CD}{b}&=\color{#3A9A38}{{\parallel}\overrightarrow{u}{\parallel}}\sin\color{#FA7921}{\theta}\\\color{#3B87CD}{b}&=\color{#3A9A38}{5.8}\sin\color{#FA7921}{320^\circ}\\ \color{#3B87CD}{b}&\approx\color{#3B87CD}{-3.73}\end{align}||
Therefore, the components of vector |\overrightarrow{u}| are |(\color{#EC0000}{4.44},\color{#3B87CD}{-3.73}).|
A vector can be represented by a right triangle and the magnitude (norm) can be calculated from the components using the Pythagorean Theorem.
What is the magnitude (norm) of vector |\overrightarrow{u}|, if the horizontal component is |\color{#EC0000}{a}=\color{#EC0000}{-5.6}| and the vertical component is |\color{#3B87CD}{b}=\color{#3B87CD}{-4.2}|?
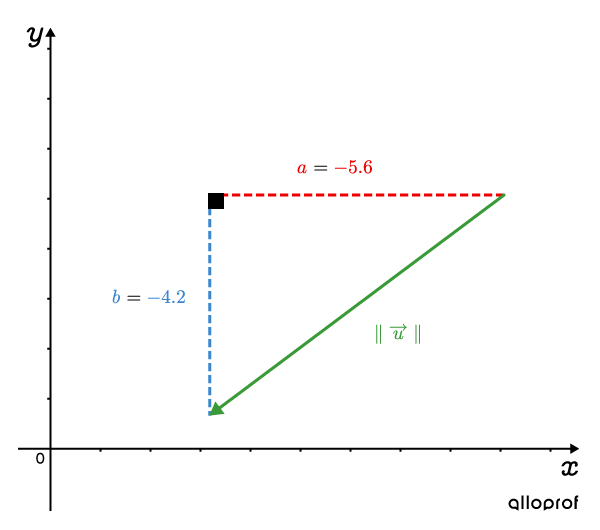
By directly applying the Pythagorean Theorem, we get:
||\begin{align}\color{#3A9A38}{{\parallel}\overrightarrow{u}{\parallel}}^2&=\color{#EC0000}{a}^2+\color{#3B87CD}{b}^2\\&=(\color{#EC0000}{-5.6})^2+(\color{#3B87CD}{-4.2})^2 \\&=49\\\color{#3A9A38}{{\parallel}\overrightarrow{u}{\parallel}}&=\pm\sqrt{49}\\&=\pm7\end{align}||
|-7| is rejected as a value because the magnitude (norm) of a vector is always positive. Therefore, the magnitude of vector |\overrightarrow{u}| is |\color{#3A9A38}{{\parallel}\overrightarrow{u}{\parallel}}=\color{#3A9A38}{7}.|
If the coordinates of origin |A(x_{\small{A}},y_{\small{A}})| and end point |B(x_{\small{B}},y_{\small{B}})| of vector |\overrightarrow{AB}| are known, then the magnitude (norm) is calculated using the formula for the distance between two points.
||\begin{align}\color{#3A9A38}{{\parallel}\overrightarrow{AB}{\parallel}}&=\sqrt{\color{#EC0000}{\Delta x}^2+\color{#3B87CD}{\Delta y}^2}\\&=\sqrt{(\color{#EC0000}{x_{{\small}{B}}-x_{{\small}{A}}})^2+(\color{#3B87CD}{y_{{\small}{B}}-y_{{\small}{A}}})^2}\end{align}||
When the components |(\color{#EC0000}{a},\color{#3B87CD}{b})| of a vector |\overrightarrow{u}| are known, its direction |\color{#FA7921}{\theta}| can be determined by using trigonometric ratios.
By convention, a vector’s direction is given by the counterclockwise angle it forms with the positive |x|-axis. Vector |\overrightarrow{u}| in the image is an example.
However, an angle can have a negative value, like vector |\overrightarrow{v}| in the same image. In those cases, the vector’s direction is the clockwise angle it forms with the positive |x|-axis.

Consider vector |\overrightarrow{u}|, where the components |\color{#EC0000}{a}| and |\color{#3B87CD}{b}| are known. To calculate the vector’s direction |\color{#FA7921}{\theta}| use the inverse of the tangent function.
However, the |\arctan| function only gives angle values between |-90^\circ| and |90^\circ.| It is the reason why |\color{#EFC807}{\theta\ '}| is used to represent the result of the |\arctan| function and |\color{#FA7921}{\theta}| is used to represent the direction of vector |\overrightarrow{u}.| Therefore, from the trigonometric relations in a vector, we have:
||\tan\color{#EFC807}{\theta\ '}=\dfrac{\color{#3B87CD}{b}}{\color{#EC0000}{a}}||
By isolating |\color{#EFC807}{\theta\ '},| we obtain the following formula.
||\color{#EFC807}{\theta\ '} =\arctan\left(\dfrac{\color{#3B87CD}{b}}{\color{#EC0000}{a}}\right)||
It is a good idea to sketch the vector according to the sign of its components |\color{#EC0000}{a}| and |\color{#3B87CD}{b}.| Using the sketch and the table below, apply the necessary corrections to angle |\color{#EFC807}{\theta\ '}| to find the direction |\color{#FA7921}{\theta}| of vector |\overrightarrow{u}| with a measure between |0^\circ| and |360^\circ.|
| |a>0| | |a<0| | |
|---|---|---|
| |b>0| |
|\color{#FA7921}{\theta}=\color{#EFC807}{\theta\ '}+0^\circ|  |
|\color{#FA7921}{\theta}=\color{#EFC807}{\theta\ '}+180^\circ|  |
| |b<0| |
|\color{#FA7921}{\theta}=\color{#EFC807}{\theta\ '}+360^\circ| 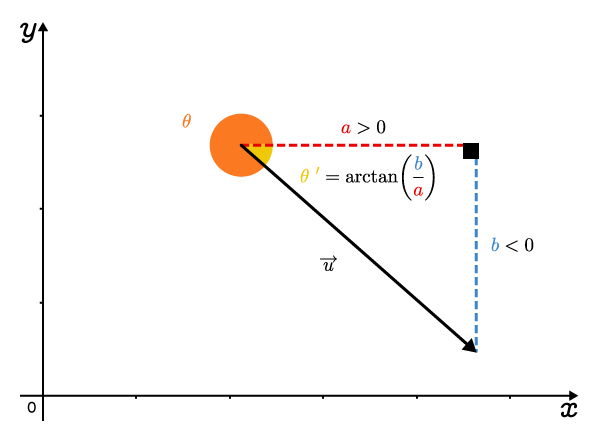 |
|\color{#FA7921}{\theta}=\color{#EFC807}{\theta\ '}+180^\circ|  |
To determine a vector’s direction |\color{#FA7921}{\theta}| from its components, take the following steps:
-
Determine the vector’s components |\color{#EC0000}{a}| and |\color{#3B87CD}{b}|.
-
Calculate the vector’s direction |\color{#EFC807}{\theta\ '}| using the formula |\color{#EFC807}{\theta\ '}=\arctan\left(\dfrac{\color{#3B87CD}{b}}{\color{#EC0000}{a}}\right).|
-
Check the sign of the components |\color{#EC0000}{a}| and |\color{#3B87CD}{b}| and apply the correction to the value of |\color{#EFC807}{\theta\ '},| if needed.
-
Give the vector’s direction |\color{#FA7921}{\theta}|.
What is the direction of the following vector |\overrightarrow{AB}|?
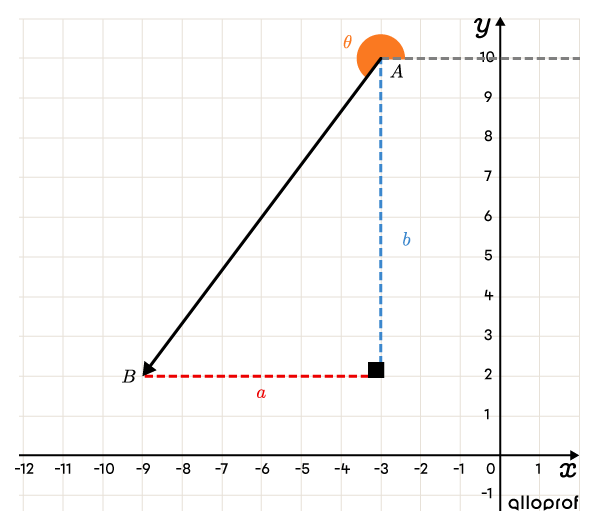
-
Determine the vector’s components |a| and |b|
The coordinates of point |A| are |(-3,10)| and point B are |(-9,2).| So, we have:
||\begin{align}\overrightarrow{AB}&=(\color{#EC0000}{a},\color{#3B87CD}{b})\\&=(x_{\small{B}}-x_{\small{A}},y_{\small{B}}-y_{\small{A}})\\&=(-9--3,2-10)\\&=(\color{#EC0000}{-6},\color{#3B87CD}{-8})\end{align}|| -
Calculate the vector’s direction |\theta\ '|
||\begin{align}\color{#EFC807}{\theta\ '} &=\arctan\left(\dfrac{\color{#3B87CD}{b}}{\color{#EC0000}{a}}\right)\\ &=\arctan\left(\dfrac{\color{#3B87CD}{-8}}{\color{#EC0000}{-6}}\right)\\\\ \color{#EFC807}{\theta\ '} &\approx \color{#EFC807}{53.13^\circ} \end{align}|| -
Check the sign of components |a| and |b| and apply the correction to the value of |\theta\ '|
Since |\color{#EC0000}{a}<0| and |\color{#3B87CD}{b}<0,| |180^\circ| has to be added to |\color{#EFC807}{\theta\ '}| to get the direction |\color{#FA7921}{\theta}.| We have:
||\begin{align}\color{#FA7921}{\theta}&=\color{#EFC807}{\theta\ '} +180^\circ\\&=\color{#EFC807}{53.13^\circ}+180^\circ\\&=\color{#FA7921}{233.13^\circ}\end{align}|| -
Give the vector’s direction |\theta|
The direction of |\color{#FA7921}{\theta}| of vector |\overrightarrow{AB}=(\color{#EC0000}{-6},\color{#3B87CD}{-8})| is |\color{#FA7921}{233.13^\circ}.|
Pour valider ta compréhension à propos des vecteurs de façon interactive, consulte la MiniRécup suivante :
