The energy efficiency of a machine or a technological system is the percentage of the energy consumed by a system that will be transformed into useful energy.
It is nearly impossible to have a system with an energy efficiency of |100\ \%| . This would mean that a device uses all the energy it consumes to transform it into the desired form of energy. For example, a light bulb would have to use all the electrical energy it consumes to transform it into light energy. However, there is always a certain amount of energy that will not be transformed into useful energy; this greatly varies depending on the device used.
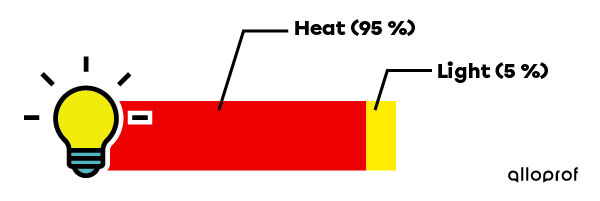
In the case of an incandescent bulb, we want to transform electrical energy into light energy. However, only |5\ \%| of electrical energy is transformed into light energy, which corresponds to the energy efficiency of this type of bulb. The rest of the energy has not disappeared: it is transformed into heat.
The following diagram illustrates the energy efficiency of an incandescent bulb.
The efficiency of a device can be determined by determining its energy efficiency, that is, its ability to transform a quantity of consumed energy into useful energy in order to reduce energy losses. To do this, we use the following equation.
|\text{Energy efficiency}=\dfrac{E_\text{useful}\text{(J)}}{E_\text {consumed}\text{(J)}}\times 100|
where
|E_\text {useful}| represents the amount of useful energy |\text{(J)}|
|E_\text {consumed}| represents the amount of energy consumed |\text{(J)}|
The energy efficiency of a device can never exceed |100\ \%|.
According to the law of conservation of energy, energy cannot be created. This means that a system cannot provide a greater quantity of useful energy than the quantity of energy it has consumed.
The energy used to turn the wheels of a car over a distance of |100\ \text{m}| is |9\ 800\ \text{J}|. However, the energy consumed by the motor during this motion is |70\ 000\ \text{J}|. What is the energy efficiency of the car?
Amount of energy consumed = |70\ 000\ \text{J}|
Amount of useful energy = |9\ 800\ \text{J}|
Energy efficiency = ?
|\begin{align}\text {Energy efficiency}&=\dfrac{E_\text {useful }\text{(J)}}{E_\text {consumed}\text{(J)}}\times 100 \\ \text{Energy efficiency}&=\dfrac{\text {9 800 J}}{\text {70 000 J}}\times 100 \\ \text{Energy efficiency}&=14 \: \% \end{align}|
The energy efficiency of the car is therefore |14\ \%|.
During a transformation of energy by a system, there is often energy that is dissipated in the environment. Energy that is not used by the system is called dissipated energy. The amount of useful energy to perform a job is therefore only a portion of the total amount of consumed energy. The rest is dissipated into the environment or turned into some unwanted form of energy.
In the case of a simple machine, friction causes a form of energy that is not useful. In fact, part of the energy will be transformed into the unwanted thermal energy produced by friction, rather than into the useful form of mechanical energy obtained in the form of displacement.
According to the law of conservation of energy, there is no loss of energy.
This is why the amount of energy consumed is equal to the sum of useful energy and dissipated energy.
||\text{Energy consumed}=\text{Useful energy}+\text{Energy dissipated}||
In the previous example, the car consumed |\text {70 000 J}| of fossil fuel energy. Some of this energy, |\text {9 800 J}|, was transformed into mechanical energy to allow the wheels to turn. The rest of the energy was lost to the surroundings in various forms. Here is a diagram to illustrate this situation.

The following calculation demonstrates that the law of conservation of energy applies.
|\begin{align}
\text{Energy consumed}&=\text{Useful energy}+\text{Energy dissipated}\\
70 000\ \text{J}&=9800\ \text{J}+60 200\ \text{J}\\
70 000\ \text{J}&=70\ 000\ \text{J}
\end{align}|
Since the sum of useful energy and dissipated energy is equal to the amount of energy consumed, we can say that the law of conservation of energy is respected. No energy has been created or destroyed by the car.
A DVD player consumes |54\ 000\ \text{J}| of electrical energy to run for one hour. If it dissipates |16\ 800\ \text{J}| in thermal energy, what is its energy efficiency?
Amount of energy consumed = |54\ 000\ \text{J}|
Amount of useful energy = ?
Amount of dissipated energy = |16\ 800\ \text{J}|
Energy efficiency = ?
- Determine how much energy is useful
|\begin{align}
E_\text{consumed} &= E_\text{useful} + E_\text{dissipated}\\
E_\text{useful} &= E_\text{consumed} - E_\text{dissipated}\\E_\text{useful} &= \text{54 000 J - 16 800 J}\\
E_\text{useful} &= \text{37 200 J} \end{align}| - Determine the energy efficiency of the device
| \begin{align}\text {Energy efficiency}&= \dfrac{E_\text {useful}\text{(J)}}{E_\text {consumed}\text{(J)}}\times 100\\
\text{Energy efficiency}&= \dfrac{\text {37 200 J}}{\text {54 000 J}}\times 100\\
\text{Energy efficiency} &\approx 68{.}89\ \% \end{align}|
The energy efficiency of the DVD player is approximately |68{.}89\ \%|.
To increase the energy efficiency of a device, it is necessary either to reduce the amount of energy consumed by the device, or to optimize the energy transformation so as to increase the ratio of useful energy.
The manufacturer of a water heater must ensure that heat loss of the device is minimized by insulating it as efficiently as possible when designing it.
The LED bulb is one of the most efficient bulbs on the market. In fact, its energy efficiency is on average |80\ \%|. If the bulb emitted |60\ \text{J}| of energy in light form, how much electrical energy did it consume?
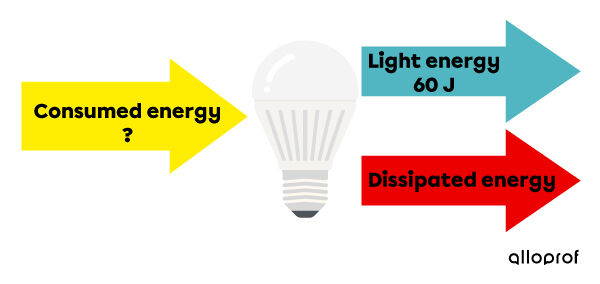
Amount of energy consumed = ?
Quantity of useful energy = |60\ \text{J}|
Energy efficiency = |80\ \%|
| \begin{align}\text {Energy efficiency}=\dfrac{E_\text {useful }\text{(J)}}{E_\text {consumed}\text{(J)}}\times 100\Rightarrow
E_\text {consumed}\text{(J)}&=\dfrac{E_\text {useful }\text{(J)}}{\text {Energy efficiency}}\times 100\\
E_\text {consumed}\text{(J)}&=\dfrac{\text {60 J}}{\text {80 %}}\times 100\\
E_\text {consumed}\text{(J)}&= \text {75 J}
\end{align}|
To produce |60\ \text{J}| of light energy, the bulb has consumed |75\ \text{J}| of electrical energy.