Le rendement énergétique d'une machine ou d'un système technologique est le pourcentage de l’énergie consommée par un système qui sera transformée en énergie utile.
Il est à peu près impossible d’avoir un système qui possède un rendement énergétique de |100\ \%|. Cela signifierait qu’un appareil utilise toute l’énergie qu’il consomme pour la transformer en la forme d’énergie souhaitée. Par exemple, il faudrait qu’une ampoule utilise toute l’énergie électrique qu’elle consomme pour la transformer en énergie lumineuse. Or, il y a toujours une certaine quantité d'énergie qui ne sera pas transformée en énergie utile, ce qui varie beaucoup selon l’appareil utilisé.
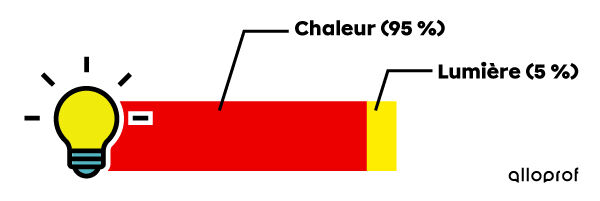
Dans une ampoule à incandescence, on désire transformer de l’énergie électrique en énergie lumineuse. Or, seulement |5\ \%| de l’énergie électrique est transformée en énergie lumineuse, ce qui correspond au rendement énergétique de ce type d’ampoule. Le reste de l’énergie n'a pas disparu : il est transformé en chaleur.
Le diagramme suivant illustre le rendement énergétique d’une ampoule à incandescence.
On peut déterminer l'efficacité d'un appareil en déterminant son rendement énergétique, c'est-à-dire sa capacité à transformer une quantité d'énergie consommée en énergie utile afin de réduire les pertes d'énergie. Pour ce faire, on utilise l'équation suivante.
|\text{Rendement énergétique}=\dfrac{E_\text{utile}\text{(J)}}{E_\text {consommée}\text{(J)}}\times 100|
où
|E_\text {utile}| représente la quantité d’énergie utile |\text{(J)}|
|E_\text {consommée}| représente la quantité d’énergie consommée |\text{(J)}|
Le rendement énergétique d’un appareil ne peut jamais dépasser |100\ \%|.
Selon la loi de la conservation de l’énergie, on ne peut pas créer de l'énergie. Un système ne peut donc pas fournir une quantité d'énergie utile plus grande que la quantité d'énergie qu'il a consommée.
L'énergie utilisée pour faire tourner les roues d'une voiture sur une distance de |100\ \text{m}| est de |9\ 800\ \text{J}|. Or, l'énergie consommée par le moteur lors de ce déplacement est de |70\ 000\ \text{J}|. Quel est le rendement énergétique de la voiture?
Quantité d’énergie consommée = |70\ 000\ \text{J}|
Quantité d’énergie utile = |9\ 800\ \text{J}|
Rendement énergétique = ?
|\begin{align}\text {Rendement énergétique}&=\dfrac{E_\text {utile }\text{(J)}}{E_\text {consommée}\text{(J)}}\times 100 \\ \text{Rendement énergétique}&=\dfrac{\text {9 800 J}}{\text {70 000 J}}\times 100 \\ \text{Rendement énergétique}&=14 \: \% \end{align}|
Le rendement énergétique de la voiture est donc de |14\ \%|.
Lors d'une transformation de l'énergie par un système, il y a souvent de l'énergie qui est dissipée dans l'environnement. On appelle énergie dissipée l’énergie qui n’est pas utilisée par le système. La quantité d'énergie utile pour effectuer un travail ne représente donc qu'une portion de la quantité totale d'énergie consommée. Le reste est dissipé dans l'environnement ou encore transformé en une forme d'énergie non désirée.
Dans le cas d'une machine simple, le frottement est à l'origine d'une forme d'énergie qui n'est pas utile. En effet, une partie de l'énergie sera transformée en une forme non désirée, l’énergie thermique produite par le frottement, plutôt qu’en énergie utile, l’énergie mécanique obtenue sous forme de déplacement.
Selon la loi de la conservation de l’énergie, il n'y a aucune perte d'énergie. C’est pourquoi on considère que l’énergie consommée est égale à la somme de l’énergie utile et de l’énergie dissipée.
||\text{Énergie consommée}=\text{Énergie utile}+\text{Énergie dissipée}||
Dans l’exemple précédent, la voiture a consommé |\text {70 000 J}| d’énergie fossile. Une partie de cette énergie, |\text {9 800 J}|, a été transformée en énergie mécanique pour permettre aux roues de tourner. Le reste de l’énergie a été dissipé dans l’environnement sous différentes formes. Voici un schéma qui illustre cette situation.

On peut démontrer que la loi de la conservation de l’énergie est respectée en faisant le calcul suivant.
|\begin{align}
\text{Énergie consommée}&=\text{Énergie utile}+\text{Énergie dissipée}\\
70\ 000\ \text{J}&=9\ 800\ \text{J}+60\ 200\ \text{J}\\
70\ 000\ \text{J}&=70\ 000\ \text{J}
\end{align}|
Puisque la somme de l’énergie utile et de l’énergie dissipée est égale à l'énergie consommée, on peut dire que la loi de la conservation de l’énergie est respectée. Aucune énergie n’a été créée ni détruite par la voiture.
Un lecteur DVD consomme |54\ 000\ \text{J}| d’énergie électrique pour fonctionner pendant une heure. S’il dissipe |16\ 800\ \text{J}| en énergie thermique, quel est son rendement énergétique?
Quantité d’énergie consommée = |54\ 000\ \text{J}|
Quantité d’énergie utile = ?
Quantité d’énergie dissipée = |16\ 800\ \text{J}|
Rendement énergétique = ?
1. Déterminer quelle est la quantité d’énergie utile
|\begin{align}
E_\text{consommée} &= E_\text{utile} + E_\text{dissipée}\\
E_\text{utile} &= E_\text{consommée} - E_\text{dissipée}\\E_\text{utile} &= \text{54 000 J - 16 800 J}\\
E_\text{utile} &= \text{37 200 J}
\end{align}|
2. Déterminer le rendement énergétique de l’appareil
| \begin{align}\text {Rendement énergétique}&= \dfrac{E_\text {utile }\text{(J)}}{E_\text {consommée}\text{(J)}}\times 100\\
\text{Rendement énergétique}&= \dfrac{\text {37 200 J}}{\text {54 000 J}}\times 100\\
\text{Rendement énergétique} &\approx 68{,}89\ \%
\end{align}|
Le rendement énergétique du lecteur DVD est d’environ |68{,}89\ \%|.
Pour augmenter le rendement énergétique d'un appareil, il faut soit diminuer la quantité d’énergie consommée par celui-ci, soit optimiser la transformation d'énergie de façon à augmenter la proportion d'énergie utile.
Lorsqu'une compagnie fabrique un chauffe-eau, elle doit s'assurer de minimiser les pertes de chaleur en isolant le chauffe-eau de la manière la plus efficace possible.
L’ampoule à DEL est l’une des ampoules les plus efficaces sur le marché. En effet, son rendement énergétique est en moyenne de |80\ \%|. Si l’ampoule a émis |60\ \text{J}| d’énergie sous forme lumineuse, quelle quantité d’énergie électrique a-t-elle consommée?
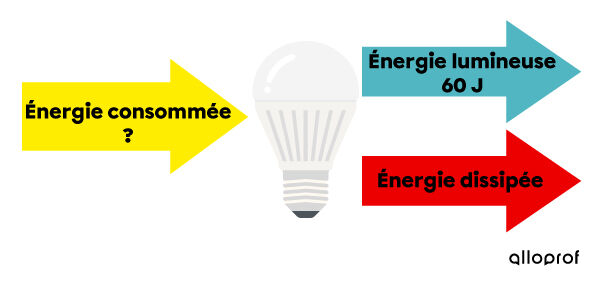
Quantité d’énergie consommée = ?
Quantité d’énergie utile = |60\ \text{J}|
Rendement énergétique = |80\ \%|
| \begin{align}\text {Rendement énergétique}=\dfrac{E_\text {utile }\text{(J)}}{E_\text {consommée}\text{(J)}}\times 100\Rightarrow
E_\text {consommée}\text{(J)}&=\dfrac{E_\text {utile }\text{(J)}}{\text {Rendement énergétique}}\times 100\\
E_\text {consommée}\text{(J)}&=\dfrac{\text {60 J}}{\text {80 %}}\times 100\\
E_\text {consommée}\text{(J)}&= \text {75 J}
\end{align}|
Pour produire |60\ \text{J}| d’énergie lumineuse, l’ampoule a consommé |75\ \text{J}| d’énergie électrique.