Mass represents the amount of matter in a substance or object. The mass is usually measured in grams |(\text{g}).|
To measure the mass of a substance or object, use a balance scale. Here are two models.

The gram |(\text{g})| is the basic unit of mass, but there are other units for expressing it. Here is a table showing the most common units of measurement for mass.
| Prefix | kilo- | hecto- | deca- | deci- | centi- | milli- | |
|---|---|---|---|---|---|---|---|
| Mass unit | kilogra, |(\text{kg})| |
hectogram |(\text{hg})| |
decagram |(\text{dag})| |
gram |(\text{g})| |
decigram |(\text{dg})| |
centigram |(\text{cg})| |
milligram |(\text{mg})| |
| Value equivalent to |1\ \text{g}| | |0{.}001\ \text{kg}| | |0{.}01\ \text{hg}| | |0{.}1\ \text{dag}| | |1\ \text{g}| | |10\ \text{dg}| | |100\ \text{cg}| | |1\ 000\ \text{mg}| |
The choice of the unit of measurement is based on the object to be measured. The unit should be chosen so that the value is neither too large nor too small.
-
The mass of this fly is |0{.}015\ \text{g}.|
It is better to use milligrams.
The mass of this fly is |15\ \text{mg}.|

AvishekS, Shutterstock.com
-
The mass of one of these tissue boxes is |175\ \text{g}.|
Gram is the appropriate unit.

Africa Studio, Shutterstock.com
-
The mass of this bowling ball is |5\ 450\ \text{g}.|
Using kilograms is more appropriate.
The mass of this bowling ball is |5{.}450\ \text{kg}.|

Aleksandar Karanov, Shutterstock.com
The mass of a substance varies with the amount of matter it contains. This material also occupies a space – a volume.
Wrongly, we tend to believe that the larger an object, the greater its mass, but this is not always the case.
In order to compare the mass of different substances having the same volume, it is necessary to know what substances they are.
When carrying a box full of books and another identical box full of feathers, we find that the feather box is much lighter than the book box.
The two boxes have the same volume but different masses, since they do not contain the same substance.

In the lab, the mass of |100{.}0\ \text{mL}| of water and the mass of |100{.}0\ \text{mL}| palm-based vegetable oil is measured. The following data is obtained.
| Substance | Volume |(\text{mL})| |
Mass |(\text{g})| |
|---|---|---|
| Water | |100{.}0| | |100{.}0| |
| Palm-based vegetable oil | |100{.}0| | |92{.}5| |
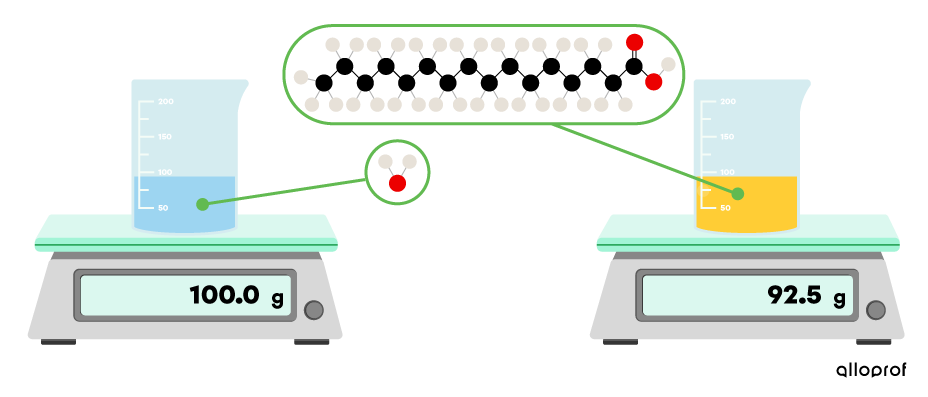
Even though the two substances have the same volume, their chemical composition is different. The number of atoms, the types of atoms and the distance between molecules cause the density of substances to vary.
For example, water is a small molecule consisting of 3 atoms: 2 hydrogens and 1 oxygen. Palmitic acid (component of palm-based vegetable oil) is a large molecule consisting of 50 atoms: 32 hydrogens, 16 carbons, and 2 oxygens.
Since the molecules of water and palm-based vegetable oil are very different, these two substances will not have the same properties. Likewise, water and oil do not have the same quantity of matter for the same volume.
In the end, there is less matter in |100{.}0\ \text{mL}| palm-based vegetable oil than in |100{.}0\ \text{mL}| of water. This explains why their mass is different.
The weight of an object represents the measure of the force with which the Earth (or another celestial body) attracts it. Weight is measured in newtons |(\text{N}).|
To determine the weight of an object, use a dynamometer.
The dynamometer features a spring that extends when an object is hung from it. The longer the spring stretches, the greater the weight.
There are graduations on the transparent tube, allowing the weight to be read in newtons.
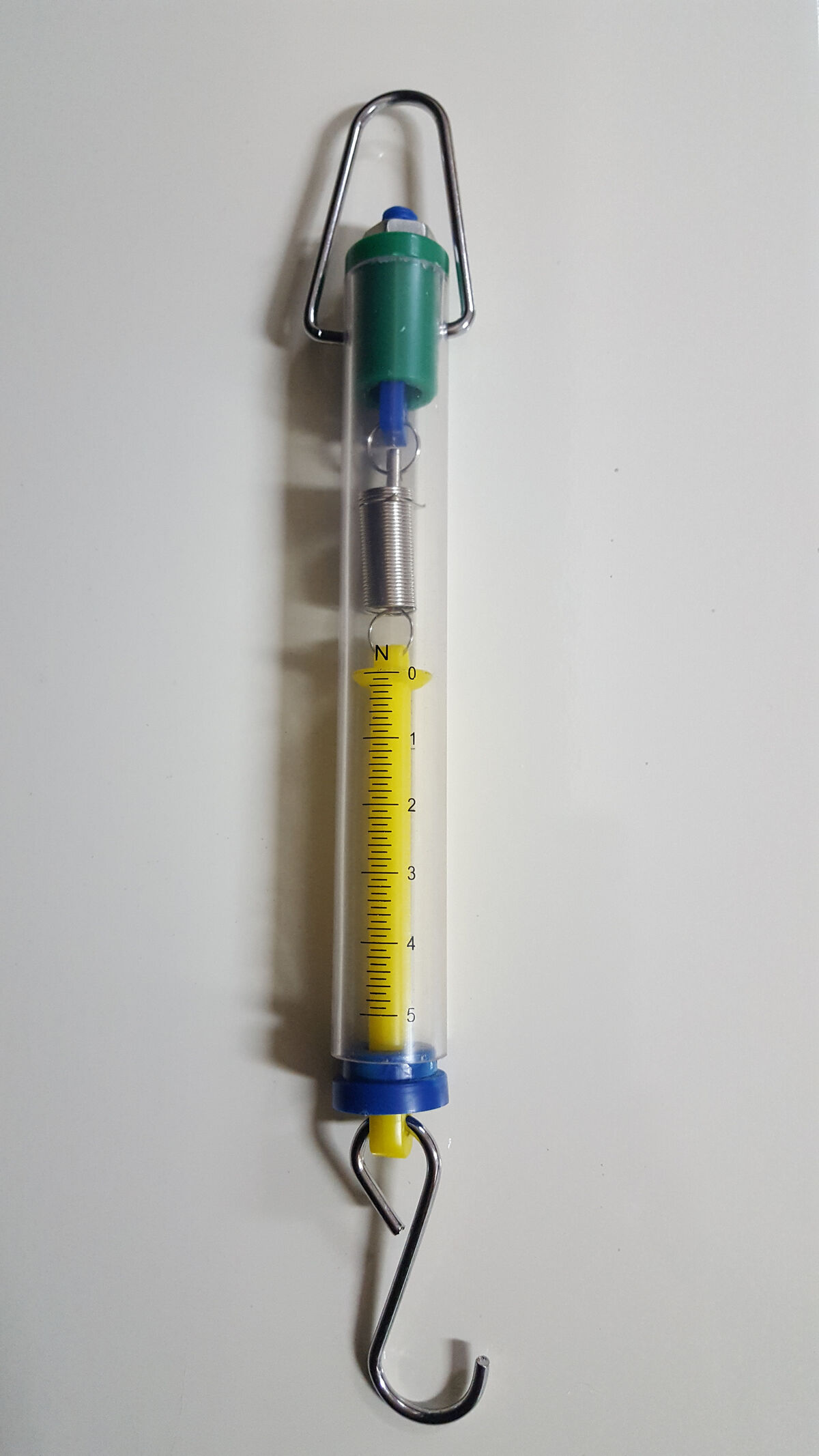
sommemambuler, Shutterstock.com
The weight of an object depends on:
-
the mass of the object: the greater the mass, the greater the weight;
-
the intensity of the gravitational field of the celestial body on which it is located: the more intense the gravitational field, the greater the weight of the object.
The following table shows the strength of the gravitational field on the surface of some of the solar system’s celestial bodies.
| Celestial bodies | Gravitational field strength |(\text{N/kg})| |
|---|---|
| Sun | |274| |
| Moon | |1{.}62| |
| Mercury | |3{.}70| |
| Venus | |8{.}87| |
| Earth | |9{.}81| |
| Mars | |3{.}72| |
| Jupiter | |24{.}79| |
| Saturn | |10{.}44| |
| Uranus | |8{.}87| |
| Neptune | |11{.}15| |
The mass of an object is its amount of matter. This is fixed regardless of which celestial object the object is located on. To determine weight, it is necessary to take into account the strength of the gravitational field of the celestial body on which the object is located.
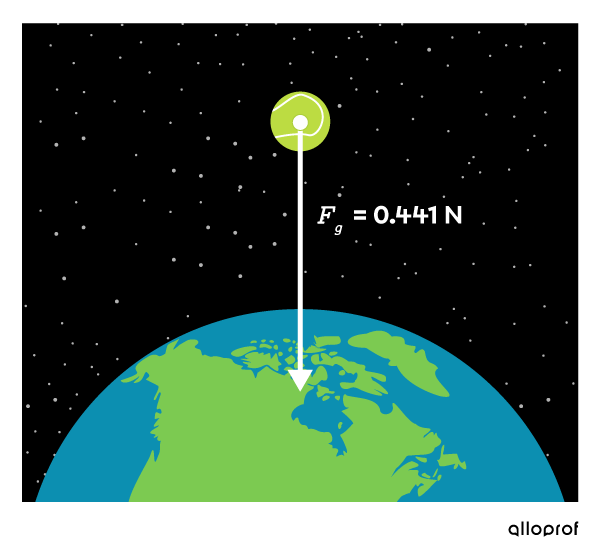
This tennis ball |45{.}0\ \text{g}| always has the same amount of atoms no matter where it is located in space.
The weight of the tennis ball on Earth is |0{.}441\ \text{N}.|
The Moon does not attract the tennis ball as strongly as Earth does, because its gravitational field is weaker.
The weight of the tennis ball is lighter on the Moon, that is |0{.}0729\ \text{N}.|
The mass of the tennis ball, which is |45{.}0\ \text{g}|, remains constant.
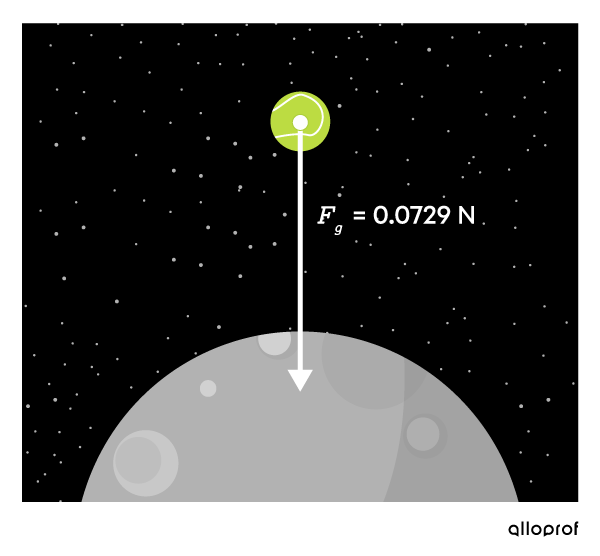
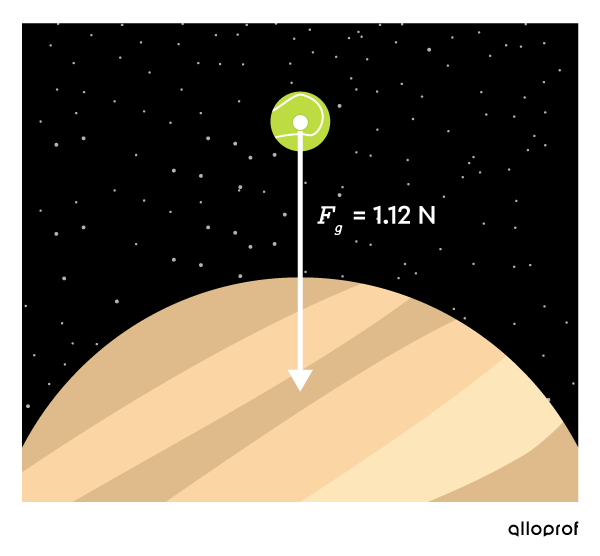
Jupiter attracts the tennis ball with greater force than the Earth, because its gravitational field is stronger.
The weight of the tennis ball is greater on Jupiter, it is |1{.}12\ \text{N}.|
The mass of the tennis ball, which is |45{.}0\ \text{g}|, remains constant.
To calculate the weight of an object, we use the following formula.
||F_g=mg||
where
|F_g| represents weight (a measure of gravitational force) in newtons |(\text{N})|
|m| represents the mass in kilograms |(\text{kg})|
|g| represents the strength of the gravitational field in newtons/kilogram |(\text{N/kg})|
A |150\ 000\ \text{g}| dolphin is swimming in the ocean.
How much does this dolphin weigh?
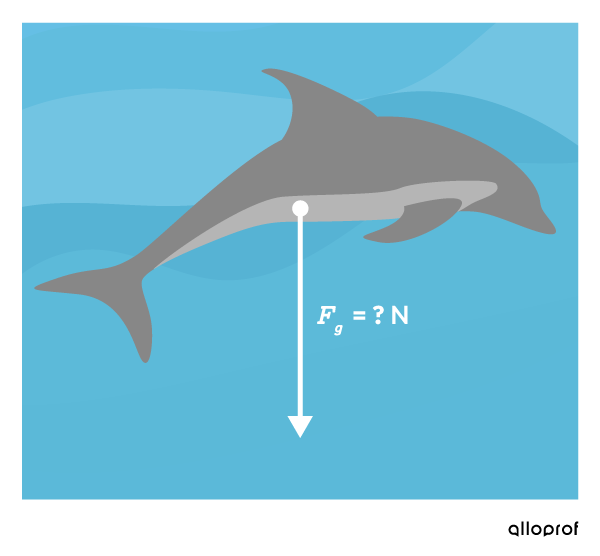
Since the dolphin swims in the ocean, we can deduce that this situation takes place on Earth and that we will use the strength of the Earth’s gravitational field |(g_{Earth}=9{.}81\ \text{N/kg})|.
First, identify the given values.
|\begin{align}
&F_g=?\ \text{N}\\
&m=150\ 000\ \cancel{\text{g}} \times \dfrac{1\ \text{kg}}{1\ 000\ \cancel{\text{g}}}=150{.}000\ \text{kg}\\
g&=9{.}81\ \text{N/kg} \end{align}|
Then, identify the formula to use and replace the variables with the values given.
|\begin{align}
F_g&=mg\\
F_g&=150{.}000\ \text{kg} \times 9{.}81\ \text{N/kg}\\
F_g&=1\ 471{.}5\ \text{N}
\end{align}|
The weight of the dolphin is |1\ 470\ \text{N},| or around |1{.}47\times10^3\ \text{N}| when taking significant figures into account
The Perseverance astromobile weighs |10\ 300\ \text{N}| on Earth.
What is the weight of Perseverance on Mars |(g_{Mars} = 3{.}72\ \text{N/kg})|?

Dima Zel, Shutterstock.com
In this case, it is necessary to find the mass of the planetary rover since it is the same on Earth as it is on Mars. This mass will then be used to determine the weight of the rover on Mars.
First, identify the given values.
|\begin{align}
F_{g\ Earth}&= 10\ 300\ \text{N}\\
m&=?\ \text{kg}\\
g_{Earth}&=9{.}81\ \text{N/kg}
\end{align}|
Then, identify the formula to use, isolate the variable |m|, and insert the values.
|\begin{align}
F_{g\ Earth}&=mg_{Earth}\\
m&=\dfrac{F_{g\ Earth}}{g_{Earth}}\\
m&=\dfrac{10\ 300\ \text{N}}{9{.}81\ \text{kg}}\\
m&\approx1\ 050\ \text{kg}
\end{align}|
Once the mass of the planetary rover has been found, it is possible to find |F_{g\ Mars}.|
First, identify the given values.
|\begin{align}
F_{g\ Mars}&= ?\ N\\
m&\approx1\ 050\ \text{kg}\\
g_{Mars}&=3{.}72\ \text{N/kg}
\end{align}|
Then, identify the formula to use and insert the values.
|\begin{align}
F_{g\ Mars}&=mg_{Mars}\\
F_{g\ Mars}&=1\ 050\ \text{kg} \times 3{.}72\ \text{N/kg}\\
F_{g\ Mars}&\approx3\ 906\ \text{N}
\end{align}|
The weight of Perseverance on Mars is |3\ 906\ \text{N},| or around |3{,}91\times10^3\ \text{N}| when taking significant figures into account.
This value is consistent since Perseverance's weight on Mars is lighter than its weight on Earth, where the gravitational field is stronger.
In a vacuum, two bodies will tend to approach each other until they collide. The gravitational force is what attracts the two bodies to each other.
Gravitational force is the physical phenomenon that causes the mutual attraction between two bodies. The magnitude of this force depends on the mass of the bodies and the distance separating them. The gravitational force changes as follows:
-
The greater the mass of the bodies, the greater the gravitational force between the two bodies.
-
The closer the bodies are to each other, the greater the gravitational force between the two bodies.
Bodies tend to deform spacetime with their mass, which leads to their attraction.
The image opposite shows the deformation of spacetime (gridded surface) with three balls. The more massive ball distorts spacetime even more.
