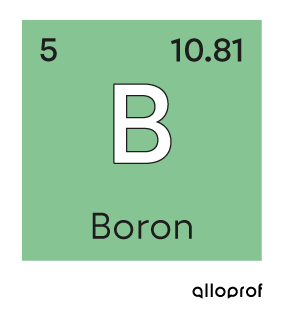Atomic mass is the mass of an atom. It can be measured in grams |\text{(g)}| or in atomic mass units |\text{(u or amu)}.|
The atomic mass includes the mass of all the neutrons and protons in an atom’s nucleus. The mass of the electrons is not considered because they are about 2 000 times lighter than protons and neutrons. Their mass would have very little influence on an atom’s total mass.
| Neutron mass |\text{(g)}| |
Proton mass |\text{(g)}| |
Electron mass |\text{(g)}| |
|---|---|---|
| |1.675 \times 10^{-24}| | |1.673 \times 10^{-24}| | |9.109 \times 10^{-28}| |
Atomic mass can be measured in grams |\text{(g)},| but the values obtained are extremely small. For that reason, it is easier to use the atomic mass units |\text{(u)}| in calculations.
|1\ \text{u}=1.66\times10^{-24}\ \text{g}|
By convention, this value is one-twelfth of the atomic mass of carbon |(1\ \text{u}= \dfrac{1}{12} \times m_C).| When the atomic mass unit is defined in relation to the mass of a carbon atom, it is called the relative atomic mass.
A potassium-39 atom |(^{39} \text{K})| has a relative atomic mass of |39.0\ \text{u}.| What is its atomic mass in grams?
The data given in the statement and the conversion factor are as follows:
|\begin{align}1\ \text{u} &= 1.66 \times 10^{-24}\ \text{g}\\39.0\ \text{u}&= ?\end{align}|
The cross multiplication method can be used to calculate the result:
|\begin{align}m_{\text{K}}&=\dfrac{(39.0\ \cancel{\text{u}}) \times (1.66 \times 10^{-24}\ \text{g})}{1\ \cancel{\text{u}}} \\m_{\text{K}}&\approx (6.47 \times 10^{-23}\ \text{g})\end{align}|
The atomic mass of a potassium-39 atom |(^{39} \text{K})| is approximately |6.47 \times 10^{-23}\ \text{g}.|
A nitrogen atom has an atomic mass of |2.32 \times 10^{-23}\ \text{g}.| What is its relative atomic mass in atomic mass units |\text{u}|?
The data given in the statement and the conversion factor are as follows:
|\begin{align}1\ \text{u} &= 1.66 \times 10^{-24}\ \text{g}\\?&= 2.32 \times 10 ^{-23}\ \text{g}\end{align}|
The cross multiplication method can be used to calculate the result:
|\begin{align}m_{\text{N}}&=\dfrac{(1\ \text{u}) \times (2.32 \times 10^{-23}\ \cancel{\text{g}})}{1.66 \times 10^{-24}\ \cancel{\text{g}}} \\m_{\text{N}}&\approx 14.0\ \text{u}\end{align}|
The relative atomic mass of this nitrogen atom is approximately |14.0\ \text{u}.|
For clarity, the term atomic mass refers to the mass of an atom expressed in grams |\text{(g)},| and the term relative atomic mass refers to the value expressed in atomic mass units |\text{(u or amu)}.|
Elements are characterized by their atomic number |\text{(Z)}| and their mass number.
The mass number |(\text{A})| is the total number of neutrons and protons in an atom’s nucleus.
A nitrogen-14 |(^{14}\text{N})| atom contains 7 protons, 7 neutrons and 7 electrons.
-
It has 7 protons, so its atomic number |\text{(Z)}| is 7.
-
However, its mass number |\text{(A)}| is 14, because it has 7 protons and 7 neutrons |(\text{A}=7+7=14).| This is why it is called nitrogen-14 |(^{14}\text{N}).|
In nature, there are different types of elements. Some atoms have the same atomic number but a different number of neutrons. These atoms are called isotopes.
Isotopes are atoms that have the same atomic number but different mass numbers. In other words, isotopes have the same number of protons but a different number of neutrons. This also means that isotopes do not have the same relative atomic mass.
Isotopes are easy to distinguish using the A/Z notation.
Potassium-39 and potassium-40 are isotopes and have different mass numbers. The A/Z notation of these isotopes is as follows:
|_{19}^{39}\text{K}| and |_{19}^{40}\text{K}|
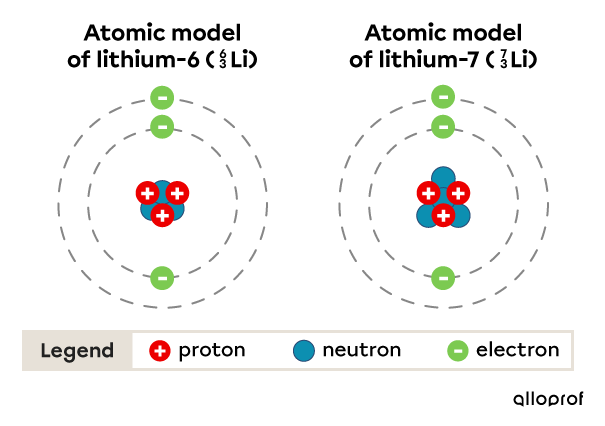
Here is the simplified atomic model of two lithium atoms. Each of these atoms has 3 protons, but they have a different number of neutrons, either 3 or 4. This means they are isotopes.
The nucleus of the second isotope contains more particles than the first, so it has a larger atomic mass than the first.
Carbon has several isotopes, the most common being carbon-12, carbon-13 and carbon-14. Here are a few characteristics of these 3 isotopes.
| Isotope | Carbon-12 | Carbon-13 | Carbon-14 |
|---|---|---|---|
| Mass number |\text{(A)}| | |12| | |13| | |14| |
| Atomic number (|\text{Z},| number of protons) | |6| | |6| | |6| |
| Number of neutrons |\text{(N)}| | |6| | |7| |
|8| |
Note that:
-
The isotopes are from the same carbon element, so all three have the same atomic number |\text{(Z)}|, and therefore 6 protons.
-
However, they have a different number of neutrons |\text{(N)}.| This is why they have different mass numbers |\text{(A)}|.
A radioactive isotope is an isotope with an unstable nucleus. This instability causes the isotope’s nucleus to degrade and emit energy.
Isotopes of the same element can have different levels of stability. The instability of a radioactive isotope’s nucleus is often caused by an excess of protons and/or neutrons.
Radioactive isotopes are naturally present in the environment, but can also be artificially generated. The radioactivity can be used in cancer treatments, to make smoke detectors, to generate electrical energy and more.
Different carbon isotopes exist in nature. Carbon-12 and carbon-13 are the most stable, while others are unstable. Carbon-14 degrades over time and its concentration diminishes. Archaeologists use this process to date remains (bones, shells, etc.) and ancient objects (wooden tools, etc.).
In nature, several isotopes of the same element can exist, each one having a different atomic mass. Some isotopes (e.g., carbon-12) are abundant while less stable isotopes (e.g., carbon-14) only exist in small quantities. The average atomic mass can be calculated for all the isotopes of an element based on their abundance in nature.
The average atomic mass is the weighted mean of the relative atomic mass of the isotopes of the same element. It is calculated based on the natural abundance of the isotopes.
The average atomic mass of an element can be found in the periodic table and is measured in atomic mass units |\text{(u)}.|

The average atomic mass of beryllium is |9.01\ \text{u}| in the periodic table. Not all periodic tables necessarily use the same format. The value of the average atomic mass can be found in different areas of the element’s square, so it is important to refer to the legend of the specific table used.
The following formula can also be used to calculate the average atomic mass.
||\overline{m} = (\%_{\text{isotope}\ 1} \times m_{\text{isotope}\ 1}) + (\%_{\text{isotope}\ 2} \times m_{\text{isotope}\ 2})+...||
where
|\overline{m}:| average atomic mass of an element
|\%_{\text{isotope}\ 1}:| natural abundance of isotope 1
|m_{\text{isotope}\ 1}:| relative atomic mass of isotope 1
|\%_{\text{isotope}\ 2}:| natural abundance of isotope 2
|m_{\text{isotope}\ 2}:| relative atomic mass of isotope 2
Using the values in the table below, determine the average atomic mass of rubidium |\text(Rb).|
| Isotope | Rubidium-85 | Rubidium-87 |
|---|---|---|
| Natural abundance of the isotope | |72.2\%| | |27.8\%| |
| Relative atomic mass of the isotope | |84.9\ \text{u}| | |86.9\ \text{u}| |
This formula can be used to determine the average atomic mass of rubidium.
||\overline{m} = (\%_{\text{isotope}\ 1} \times m_{\text{isotope}\ 1}) + (\%_{\text{isotope}\ 2} \times m_{\text{isotope}\ 2})+...||
The variables can be replaced by the values given in the table.
||\begin{align}\overline{m}_{\text{Rb}}&=(72.2\% \times84.9\ \text{u}) + (27.9\% \times 86.9\ \text{u})\\ \overline{m}_ {\text{Rb}}&\approx 85.5\ \text{u} \end{align}||
The average atomic mass of rubidium is approximately |85.5\ \text{u}.| This calculated value is consistent with the value in the periodic table.

The two stable isotopes of boron are present in the following proportions: |19.78\%| of boron-10 |(^{10}\text{B})| and |80.22\%| of boron-11 |(^{11}\text{B}).| What is the average atomic mass of boron?
The relative atomic masses of the boron isotopes are not explicitly stated. However, it is possible to estimate that boron |10| has an atomic mass of |10\ \text{u}| and that boron |11| has an atomic mass of |11\ \text{u}.|
The following formula is used to determine the average atomic mass of boron.
||\overline{m} = (\%_{\text{isotope}\ 1} \times m_{\text{isotope}\ 1}) + (\%_{\text{isotope}\ 2} \times m_{\text{isotope}\ 2})+...||
The variables can be replaced by the available values.
||\begin{align}\overline{m}_{\text{B}}&=(19.78\% \times10\ \text{u}) + (80.22\% \times 11\ \text{u})\\ \overline{m}_{\text{B}}&\approx 10.8\ \text{u}\end{align}||
The average atomic mass of boron is approximately |10.8\ \text{u}.| This calculated value is consistent with the value in the periodic table.