-
La masse molaire est la masse d’une mole d’une substance.
-
Une mole correspond à un groupe de |6{,}022\ \times 10^{23}| particules.
Le symbole de la masse molaire est |M| et son unité de mesure est le gramme par mole |\text{(g/mol).}|
La masse molaire d’un élément est aussi appelée masse molaire atomique, car elle correspond à la masse d’une mole d’atomes de cet élément.
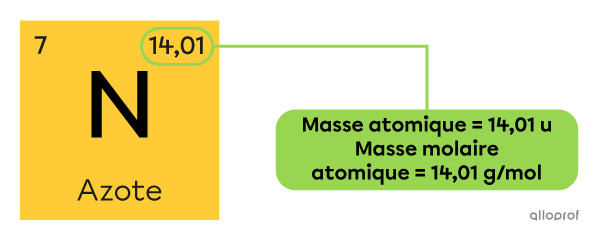
La valeur de la masse molaire atomique de chaque élément se trouve dans leur case du tableau périodique. Il s’agit de la même valeur que celle de la masse atomique exprimée en unités atomiques |\text{(u).}|
La masse atomique de l’azote |\text{(N)}| est de |14{,}01\ \text{u},| alors sa masse molaire atomique est de |14{,}01\ \text{g/mol.}| On peut l’écrire de la manière suivante.
||M_{\text{N}}=14{,}01\ \text{g/mol}||
On peut aussi dire qu’une mole d’atomes d’azote a une masse de |14{,}01\ \text{g.}|
Il est aussi possible de dire qu’un groupe de |6{,}022\times10^{23}| atomes d’azote a une masse de |14{,}01\ \text{g.}|
Pour déterminer la masse molaire d’une substance constituée de plusieurs atomes, il faut additionner la masse molaire de tous les atomes qui constituent cette substance.
Les différents types d’atomes présents et leur quantité sont indiqués dans la formule chimique de la substance.
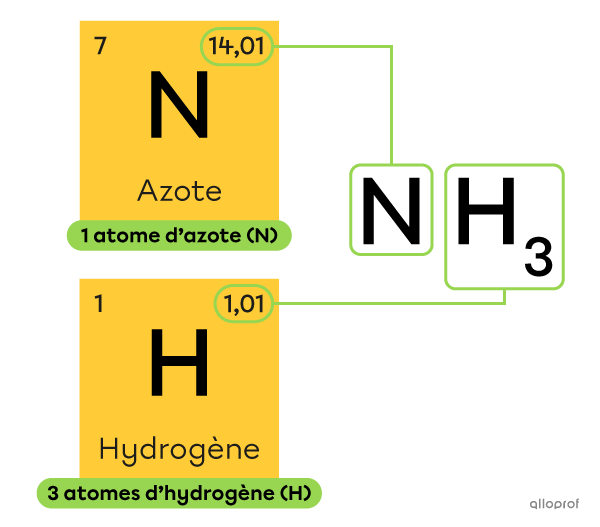
Quelle est la masse molaire de l’ammoniac |\text{(NH}_3)|?
-
On identifie les données. À l’aide du tableau périodique, on identifie la masse molaire de l’azote |\text{(N)}| et celle de l’hydrogène |\text{(H).}|
||\begin{align}M_{\text{N}} &=14{,}01\ \text{g/mol}\\ M_{\text{H}} &=1{,}01\ \text{g/mol}\\ M_{\text{NH}_3} &=\ ?\ \text{g/mol}\end{align}|| -
Dans la formule chimique de l’ammoniac |\text{(NH}_3),| on retrouve 1 atome d’azote |\text{(N)}| et 3 atomes d’hydrogène |\text{(H).}| On peut calculer la masse molaire de l’ammoniac à l’aide de l’expression suivante.
||M_{\text{NH}_3}=M_{\text{N}}+3\ M_{\text{H}}||
-
On remplace les variables et on résout l’équation.
||\begin{align}M_{\text{NH}_3} &=14{,}01\ \text{g/mol}+3\times1{,}01\ \text{g/mol}\\M_{\text{NH}_3} &=17{,}04\ \text{g/mol}\end{align}|| -
On répond à la question.
La masse molaire de l'ammoniac est de |17{,}04\ \text{g/mol.}|
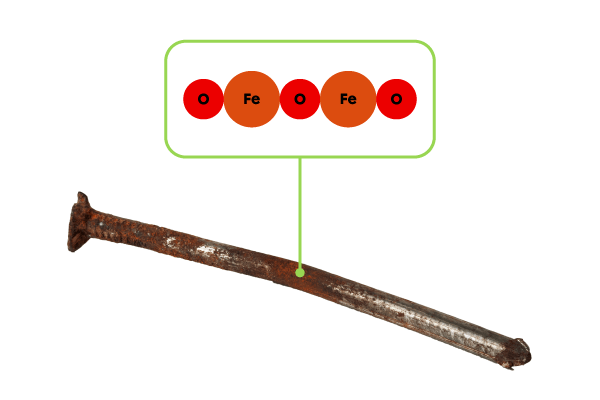
Quelle est la masse molaire du trioxyde de difer |(\text{Fe}_2 \text{O}_3),| communément appelé rouille?
-
On identifie les données. À l’aide du tableau périodique, on identifie la masse molaire du fer |(\text{Fe})| et celle de l’oxygène |(\text{O}).|
||\begin{align}M_{\text{Fe}} &=55{,}85\ \text{g/mol}\\M_{ \text{O}} &=16{,}00\ \text{g/mol}\\M_{\text{Fe}_2 \text{O}_3} &=\ ?\ \text{g/mol}\end{align}|| -
Dans la formule chimique du trioxyde de fer |(\text{Fe}_2 \text{O}_3),| on retrouve 2 atomes de fer |(\text{Fe})| et 3 atomes d’oxygène |(\text{O}).| On peut calculer la masse molaire du trioxyde de fer à l’aide de l’expression suivante.
||M_{\text{Fe}_2 \text{O}_3}=2\ M_{\text{Fe}}+3\ M_{\text{O}}|| -
On remplace les variables et on résout l’équation.
||\begin{align}M_{\text{Fe}_2 \text O_3} &=2\times55{,}85\ \text {g/mol}+3\times16{,}00\ \text{g/mol}\\M_{\text{Fe}_2 \text{O}_3} &=159{,}70\ \text{g/mol}\end{align}|| -
On répond à la question.
La masse molaire du trioxyde de fer est de |159{,}70\ \text{g/mol}.|
Quelle est la masse molaire du trisulfate de dialuminium |(\text{Al}_2(\text{SO}_4)_3)|?
-
On identifie les données. À l’aide du tableau périodique, on identifie la masse molaire de l’aluminium |(\text{Al}),| du soufre |(\text{S})| et de l’oxygène |(\text{O}).|
||\begin{align}M_{\text{Al}} &=26{,}98\ \text{g/mol}\\M_{ \text{S}} &=32{,}07\ \text{g/mol}\\M_{\text{O}} &=16{,}00\ \text{g/mol}\\M_{\text{Al}_2(\text {SO}_4)_3} &=\ ?\ \text{g/mol}\end{align}|| -
Dans la formule chimique du trisulfate de dialuminium |(\text{Al}_2(\text{SO}_4)_3),| on retrouve 2 atomes d’aluminium |(\text{Al}),| 3 atomes de soufre |(\text{S}),| et 12 atomes d’oxygène |(\text{O}).| On peut calculer la masse molaire du trisulfate de dialuminium à l’aide de l’expression suivante.
||M_{\text{Al}_2(\text{SO}_4)_3}=2\ M_{\text{Al}}\ +\ 3~M_{\text{S}}\ +~12\ M_{\text{O}}|| -
On remplace les variables et on résout l’équation.
||\begin{align}M_{\text{Al}_2(\text{SO}_4)_3} &=2\times26{,}98\ \text{g/mol}+3\times32{,}07\ \text{g/mol}+12\times16{,}00\ \text{g/mol}\\M_{\text{Al}_2(\text{SO}_4)_3} &=342{,}17\ \text{g/mol}\end{align}|| -
On répond à la question.
La masse molaire du trisulfate de dialuminium est de |342{,}17\ \text{g/mol}.|
La masse molaire |(M)| d’une substance correspond à la masse |(m)| de la substance par rapport à un nombre de moles |(n).| La relation entre |M,| |n| et |m| peut être exprimée des trois façons suivantes, selon la variable qu’on isole.
||M=\dfrac{m}{n}||
||m=nM||
||n=\dfrac{m}{M}||
où
|M\ :| masse molaire en grammes par mole |\text{(g/mol)}|
|m\ :| masse en grammes |\text{(g)}|
|n\ :| nombre de moles en moles |\text{(mol)}|
La formule |M=\dfrac{m}{n}| permet de comprendre pourquoi la masse molaire s’exprime en |\text{g/mol.}|
La masse molaire du calcium |\text{(Ca)}| correspond à une masse de |40{,}08\ \text{g}| pour |1\ \text{mol}.| On divise |40{,}08\ \bf\text{g}| par |1\ \bf\text{mol}| et on obtient des |\bf\text{g/mol}| comme unité de la masse molaire.
||M_{\text{Ca}}=\dfrac{m}{n}=\dfrac{40{,}08\ \bf\text{g}}{1\ \bf\text{mol}}=40{,}08\ \bf\text{g/mol}||
La formule |n=\dfrac{m}{M}| permet de calculer le nombre de moles d’une substance à l’aide de sa masse et de sa masse molaire.
Une salière contient |97{,}02\ \text{g}| de chlorure de sodium |(\text{NaCl}),| communément appelé sel de table. Quelle est la quantité de chlorure de sodium en nombre de moles?

Source : Adapté de HandmadePictures, Shutterstock.com
-
On identifie les données.
||\begin{align}n &=\ ?\ \text{mol}\\m &=97{,}02\ \text{g}\end{align}||
On calcule la masse molaire du chlorure de sodium |(\text{NaCl})| à l’aide de l’expression suivante.
||\begin{align}\\M_{\text{NaCl}} &=M_{\text{Na}}+M_{\text{Cl}}\\M_{\text{NaCl}} &=22{,}99\ \text{g/mol}+35{,}45\ \text{g/mol}\\M_{\text{NaCl}} &=58{,}44\ \text{g/mol}\end{align}||
-
On détermine la formule à utiliser et on isole |n.|
||M=\dfrac{m}{n} \ \Rightarrow\ n=\dfrac{m}{M}|| -
On remplace les variables et on résout l’équation.
||\begin{align}n &=\dfrac{97{,}02\ \cancel{\text{g}}}{58{,}44\ \cancel{\text{g}}\text{/mol}}\\\\n &\approx1{,}660\ \text{mol}\end{align}|| -
On répond à la question.
La salière contient environ |1{,}660\ \text{mol}| de chlorure de sodium.
La formule |m=nM| permet de calculer la masse d’une substance à l’aide du nombre de moles et de sa masse molaire.
Quelle est la masse de |2{,}25\ \text{mol}| d’eau |(\text{H}_2\text{O})|?
-
On identifie les données.
||\begin{align}m &=\ ?\ \text{g}\\n &=2{,}25\ \text{mol}\end{align}||
On calcule la masse molaire de l’eau |(\text{H}_2\text{O})| à l’aide de l’expression suivante.
||\begin{align}\\M_{\text{H}_2\text{O}} &=2\ M_{\text{H}}+M_{\text{O}}\\M_{\text{H}_2\text{O}} &=2\times1{,}01\ \text{g/mol}+16{,}00\ \text{g/mol}\\M_{\text{H}_2\text{O}} &=18{,}02\ \text{g/mol}\end{align}|| -
On détermine la formule à utiliser et on isole |m.|
||M=\dfrac{m}{n} \ \Rightarrow\ m=nM|| -
On remplace les variables et on résout l’équation.
||\begin{align}m &=2{,}25\ \cancel{\text{mol}}\times18{,}02\ \text{g/}\cancel{\text{mol}}\\m &\approx40{,}5\ \text{g}\end{align}|| -
On répond à la question.
La masse de |2{,}25\ \text{mol}| d’eau est d’environ |40{,}5\ \text{g}.|
La quantité d’une substance est parfois exprimée en nombre de particules |(N).| Pour calculer la masse d’une substance |(m)| à partir de son nombre de particules, il faut d’abord trouver le nombre de moles |(n).| Ensuite, on trouve la masse à l’aide de la formule |m=nM.|
La formule suivante permet de calculer le nombre de moles d’une substance à partir du nombre de particules et du nombre d’Avogadro.
|n=\dfrac{N}{N_{\text{A}}}|
où
|n\ :| nombre de moles en moles |(\text{mol})|
|N\ :| nombre de particules |(\text{particules})|
|N_{\text{A}}\ :| nombre d’Avogadro |(6{,}022\times10^{23}\ \text{particules/mol})|
Un échantillon comprend |1{,}402\times10^{24}| atomes de carbone |(\text{C}).|
a) Détermine le nombre de moles dans l’échantillon.
b) Détermine la masse de l'échantillon.

Source : Adapté de Eaum M, Shutterstock.com
a) Déterminer le nombre de moles dans l'échantillon
-
On identifie les données.
||\begin{align}n &=\ ?\ \text{mol}\\N &=1{,}402\times10^{24}\ \text{atomes}\\N_{\text{A}} &=6{,}022\times10^{23}\ \text{atomes/mol}\end{align}|| -
On détermine la formule à utiliser.
||n=\dfrac{N}{N_{\text{A}}}|| -
On remplace les variables et on résout l’équation.
||\begin{align}n &=\dfrac{1{,}402\times10^{24}\ {\cancel{\text{atomes}}}}{6{,}022\times10^{23}\ {\cancel{\text{atomes}}}\text{/mol}}\\\\n &\approx2{,}328\ \text{mol}\end{align}|| -
On répond à la question.
|1{,}402\times10^{24}| atomes de carbone correspondent à environ |2{,}328\ \text{mol}| de carbone.
b) Déterminer la masse de l’échantillon
-
On identifie les données. À l’aide du tableau périodique, on identifie la masse molaire du carbone|(\text{C}).|
||\begin{align}m &=\ ?\ \text{g}\\n &=2{,}328\ \text{mol}\\M_{\text{C}} &=12{,}01\ \text{g/mol}\end{align}|| -
On détermine la formule à utiliser et on isole |m.|
||M=\dfrac{m}{n} \ \Rightarrow\ m=nM|| -
On remplace les variables et on résout l’équation.
||\begin{align}m &=2{,}328\ \cancel{\text{mol}}\times12{,}01\ \text{g/}\cancel{\text{mol}}\\m &\approx27{,}96\ \text{g}\end{align}|| -
On répond à la question.
|1{,}402\times10^{24}| atomes de carbone correspondent à environ |27{,}96\ \text{g}| de carbone.