Une mesure fréquemment utilisée pour étudier la dispersion des données d'une même distribution est l'écart type.
L’écart type, habituellement noté |s| lorsqu’on étudie un échantillon et |\sigma| lorsqu’on étudie une population, est une mesure de dispersion des données autour de la moyenne.
En d'autres mots, plus l'écart type est grand, plus les données sont éloignées de la moyenne. Inversement, plus l'écart type est petit, plus les données sont concentrées autour de la moyenne.
Le calcul de l’écart type comporte plusieurs étapes qui sont résumées par les formules suivantes.
Pour un échantillon
||s= \sqrt{\dfrac{\sum(x_{i}-\overline{x})^{2}}{n-1}}||où
|\overline{x} :| moyenne de l’échantillon
|n :| taille de l’échantillon
Pour une population
||\sigma = \sqrt{\dfrac{\sum(x_i-\mu)^2}{N}}||où
|\mu :| moyenne de la population
|N :| taille de la population
|\sum| signifie qu’il faut effectuer une somme successive de plusieurs éléments.
|x_i| représente la |i^\text{e}| valeur de l’échantillon.
Dans la formule de l’écart type, ce qui se trouve sous la racine carrée se nomme la variance. Ainsi, on peut résumer le calcul de l'écart type à l’aide de l'égalité suivante.||\text{écart type} = \sqrt{\text{variance}}||Autrement dit, la variance correspond à la moyenne du carré des écarts à la moyenne.
Voici les étapes à suivre pour utiliser adéquatement les formules précédentes.
-
Vérifier si la distribution est un échantillon ou une population.
-
Déterminer la taille de la distribution.
-
Calculer la moyenne de la distribution.
-
Calculer la somme du carré des écarts à la moyenne.
-
Calculer l’écart type.
Voici les températures (en degrés Celsius), placées en ordre croissant, enregistrées chaque heure durant une journée.
|-5,| |-4,| |-4,| |-3,| |-3,| |-2,| |-1,| |0,| |0,| |1,| |2,| |3,| |3,| |4,| |4,| |6,| |7,| |8,| |9,| |10,| |10,| |11,| |11,| |12|
Détermine l’écart type de cette distribution.
-
Vérifier si la distribution est un échantillon ou une population
Il s’agit d'un échantillon, puisqu'il y a eu des moments durant la journée où la température n'a pas été notée. Ainsi, on doit utiliser la formule avec |s,| |n,| et |\overline{x}.|
-
Déterminer la taille de la distribution
Puisqu'il y a |24| heures dans une journée, cet échantillon contient |24| données |(n=24).|
-
Calculer la moyenne de la distribution
On calcule la moyenne arithmétique de toutes les données.||\begin{align}\overline{x}&=\dfrac{\left(\begin{alignat}{40}&-5&&-4&&-4&&-\ 3&&-\ 3&&-\ 2&&-\ 1&&+\ 0\\&+0&&+1&&+2&&+\ 3&&+\ 3&&+\ 4&&+\ 4&&+\ 6\\&+7&&+8&&+9&&+10&&+10&&+11&&+11&&+12\ \ \end{alignat}\right)}{24}\\&\approx3{,}29\end{align}||
-
Calculer la somme du carré des écarts à la moyenne
On calcule les écarts à la moyenne de chaque donnée, puis on les élève au carré.
| Donnée |x_i| |
Écart à la moyenne |\vert x_i-\overline{x}\vert| |
Écart à la moyenne au carré |\left(x_i-\overline{x}\right)^{2}| |
Donnée |x_i| |
Écart à la moyenne |\vert x_i-\overline{x}\vert| |
Écart à la moyenne au carré |\left(x_i-\overline{x}\right)^{2}| |
|---|---|---|---|---|---|
| |-5| | |\vert-5- 3{,}29\vert=8{,}29| | |8{,}29^2\approx68{,}72| | |3| | |\vert3- 3{,}29\vert=0{,}29| | |0{,}29^2\approx0{,}08| |
| |-4| | |\vert-4- 3{,}29\vert=7{,}29| | |7{,}29^2\approx53{,}14| | |4| | |\vert4- 3{,}29\vert=0{,}71| | |0{,}71^2\approx0{,}50| |
| |-4| | |\vert-4- 3{,}29\vert=7{,}29| | |7{,}29^2\approx53{,}14| | |4| | |\vert4- 3{,}29\vert=0{,}71| | |0{,}71^2\approx0{,}50| |
| |-3| | |\vert-3- 3{,}29\vert=6{,}29| | |6{,}29^2\approx39{,}56| | |6| | |\vert6- 3{,}29\vert=2{,}71| | |2{,}71^2\approx7{,}34| |
| |-3| | |\vert-3- 3{,}29\vert=6{,}29| | |6{,}29^2\approx39{,}56| | |7| | |\vert7- 3{,}29\vert=3{,}71| | |3{,}71^2\approx13{,}76| |
| |-2| | |\vert-2- 3{,}29\vert=5{,}29| | |5{,}29^2\approx27{,}98| | |8| | |\vert8- 3{,}29\vert=4{,}71| | |4{,}71^2\approx22{,}18| |
| |-1| | |\vert-1- 3{,}29\vert=4{,}29| | |4{,}29^2\approx18{,}40| | |9| | |\vert9- 3{,}29\vert=5{,}71| | |5{,}71^2\approx32{,}60| |
| |0| | |\vert0- 3{,}29\vert=3{,}29| | |3{,}29^2\approx10{,}82| | |10| | |\vert10- 3{,}29\vert=6{,}71| | |6{,}71^2\approx45{,}02| |
| |0| | |\vert0- 3{,}29\vert=3{,}29| | |3{,}29^2\approx10{,}82| | |10| | |\vert10- 3{,}29\vert=6{,}71| | |6{,}71^2\approx45{,}02| |
| |1| | |\vert1- 3{,}29\vert=2{,}29| | |2{,}29^2\approx5{,}24| | |11| | |\vert11- 3{,}29\vert=7{,}71| | |7{,}71^2\approx59{,}44| |
| |2| | |\vert2- 3{,}29\vert=1{,}29| | |1{,}29^2\approx1{,}66| | |11| | |\vert11- 3{,}29\vert=7{,}71| | |7{,}71^2\approx59{,}44| |
| |3| | |\vert3- 3{,}29\vert=0{,}29| | |0{,}29^2\approx0{,}08| | |12| | |\vert12- 3{,}29\vert=8{,}71| | |8{,}71^2\approx75{,}86| |
On fait ensuite la somme du carré des écarts à la moyenne.||\begin{alignat}{30}\sum(x_{i}-\overline{x})^{2}&=&&\phantom{\,+\ }68{,}72&&+53{,}14&&+53{,}14&&+39{,}56&&+39{,}56&&+27{,}98\\&&&+18{,}40&&+10{,}82&&+10{,}82&&+5{,}24&&+1{,}66&&+0{,}08\\&&&+0{,}08&&+0{,}50&&+0{,}50&&+7{,}34&&+13{,}76&&+22{,}18\\&&&+32{,}60&&+45{,}02&&+45{,}02&&+59{,}44&&+59{,}44&&+75{,}86\\&=&&\phantom{\,+\ }690{,}86\end{alignat}||
-
Calculer l’écart type
On remplace |\boldsymbol{\color{#3b87cd}n}| et |\boldsymbol{\color{#3a9a38}{\sum(x_{i}-\overline{x})^{2}}}| par leur valeur respective dans la formule de l’écart type d’un échantillon.||\begin{align}s&=\sqrt{\dfrac{\boldsymbol{\color{#3a9a38}{\sum(x_{i}-\overline{x})^{2}}}}{\boldsymbol{\color{#3b87cd}{n}}-1}}\\&=\sqrt{\dfrac{\boldsymbol{\color{#3a9a38}{690{,}86}}}{\boldsymbol{\color{#3b87cd}{24}}-1}}\\&=\sqrt{\dfrac{690{,}86}{23}}\\&\approx\sqrt{30{,}04}\\&\approx5{,}48\end{align}||
Réponse : L’écart type de cette distribution est d’environ |5{,}48\ ^\circ \text{C}.|
Remarque : Dans cet exemple, la variance est de |30{,}04.|
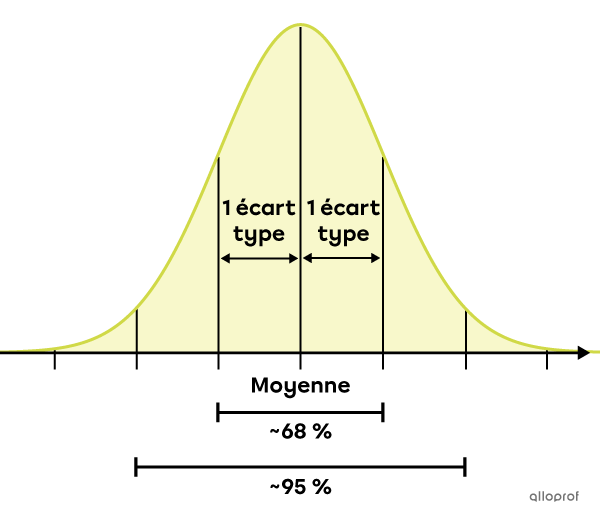
Vers 1810, après plusieurs recherches et analyses, le célèbre mathématicien Carl Friedrich Gauss établit que, parmi toutes les distributions possibles, certaines d'entre elles démontrent une dispersion des données qui tend à suivre une loi spécifique. Cette loi porte aujourd'hui le nom de loi de Gauss, ou loi normale. On parle ainsi de distribution normale.
En résumé, il démontre qu'environ |68\ \%| des données d'une distribution normale sont regroupées à |\pm1| écart type de la moyenne et qu'environ |95\ \%| des données sont situées à |\pm2| écarts types de la moyenne.