La commutativité permet de modifier l’ordre des termes dans une addition sans en changer le résultat.
Lorsque je calcule 5 + 2, j’obtiens 7.
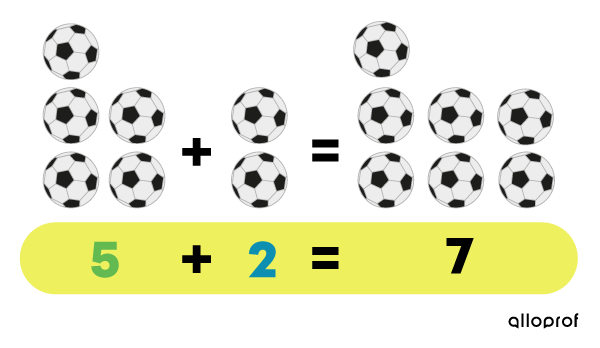
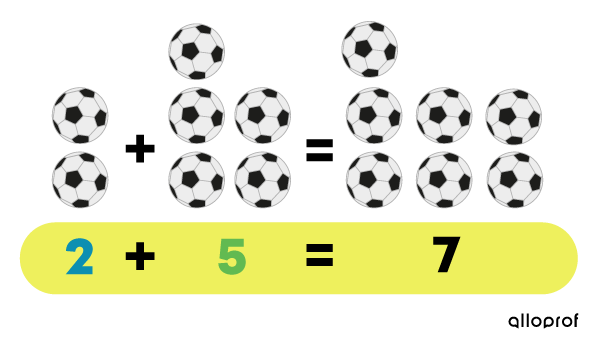
Lorsque j’inverse l’ordre des termes de cette addition, j’obtiens aussi 7.
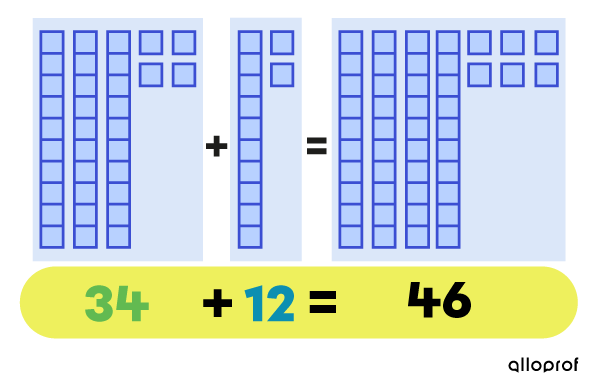
Lorsque je calcule 34 + 12, j’obtiens 46.
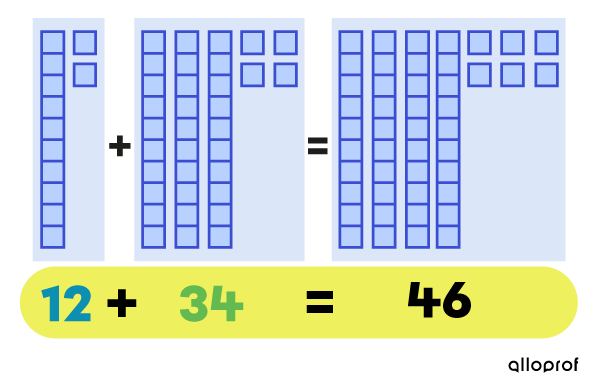
Lorsque j’inverse l’ordre des termes de cette addition, j’obtiens aussi 46.
La commutativité est une propriété d'opération qui permet de modifier l'ordre des termes dans une opération sans en changer le résultat.
La commutativité s’applique à l’addition et à la multiplication.
Lorsque je calcule 18 + 2, j’obtiens 20.
18 + 2 = 20
Lorsque j’inverse l’ordre des termes de cette addition, j’obtiens aussi 20.
2 + 18 = 20
Lorsque je calcule 3 × 5, j’obtiens 15.
3 × 5 = 15
Lorsque j’inverse l’ordre des facteurs de cette multiplication, j’obtiens aussi 15.
5 × 3 = 15
La commutativité s’applique aussi à l’addition de nombres décimaux.
Exemple :
3,2 + 4,39 = 7,59
4,39 + 3,2 = 7,59
L'associativité est une propriété d'opération qui permet de modifier l'ordre des calculs à effectuer en regroupant des nombres entre parenthèses sans changer le résultat de l'opération.
Le calcul mis entre parenthèses est celui qui doit être fait en premier dans la chaine d’opérations.
L’associativité s’applique à l’addition et à la multiplication.
Lorsque je calcule 4 + 2 + 3, j’obtiens 9.
4 + 2 + 3 = 9
Lorsque je regroupe les 2 premiers termes de cette addition, j’obtiens aussi 9.
(4 + 2) + 3 = ?
6 + 3 = ?
6 + 3 = 9
Le résultat reste encore le même lorsque je regroupe les 2 derniers termes.
4 + (2 + 3) = ?
4 + 5 = ?
4 + 5 = 9
Lorsque je calcule 2 × 5 × 4, j’obtiens 40.
2 × 5 × 4 = 40
Lorsque je regroupe les 2 premiers facteurs de cette multiplication, j’obtiens aussi 40.
(2 × 5) × 4 = ?
10 × 4 = ?
10 × 4 = 40
Le résultat reste encore le même lorsque je regroupe les 2 derniers facteurs.
2 × (5 × 4) = ?
2 × 20 = ?
2 × 20 = 40
L’associativité s’applique aussi à l’addition de nombres décimaux.
Exemple :
3,45 + 2,7 + 9,12 = 15,27
(3,45 + 2,7) + 9,12 = 15,27
3,45 + (2,7 + 9,12) = 15,27
La commutativité est une propriété d'opération qui permet de modifier l'ordre des termes dans une opération sans en changer le résultat.
La commutativité s’applique à l’addition et à la multiplication.
Lorsque je calcule 12 + 7, j’obtiens 19.
12 + 7 = 19
Lorsque j’inverse l’ordre des termes, j’obtiens aussi 19.
7 + 12 = 19
Lorsque je calcule 11 × 9, j’obtiens 99.
11 × 9 = 99
Lorsque j’inverse l’ordre des termes, j’obtiens aussi 99.
9 × 11 = 99
La commutativité s’applique aussi à l’addition et à la multiplication de nombres décimaux.
Exemples :
| Addition | Multiplication |
|---|---|
| 3,2 + 4,39 = 7,59 4,39 + 3,2 = 7,59 |
5,14 × 7,5 = 38,55 7,5 × 5,14 = 38,55 |
L'associativité est une propriété d'opération qui permet de modifier l'ordre des calculs à effectuer en regroupant des nombres entre parenthèses sans modifier le résultat de l'opération.
L’associativité s’applique à l’addition et à la multiplication.
N’oublie pas que tu dois suivre la priorité des opérations dans une chaine d’opérations. C’est pourquoi tu dois commencer par faire le calcul dans les parenthèses.
Pour en savoir plus, tu peux lire la fiche La priorité des opérations.
Lorsque je calcule 4 + 2 + 3, j’obtiens 9.
4 + 2 + 3 = 9
Lorsque je regroupe les 2 premiers termes de cette addition, j’obtiens aussi 9.
(4 + 2) + 3 = ?
6 + 3 = ?
6 + 3 = 9
Le résultat reste encore le même lorsque je regroupe les 2 derniers termes.
4 + (2 + 3) = ?
4 + 5 = ?
4 + 5 = 9
Lorsque je calcule 2 × 5 × 4, j’obtiens 40.
2 × 5 × 4 = 40
Lorsque je regroupe les 2 premiers facteurs de cette multiplication, j’obtiens aussi 40.
(2 × 5) × 4 = ?
10 × 4 = ?
10 × 4 = 40
Le résultat reste encore le même lorsque je regroupe les 2 derniers facteurs.
2 × (5 × 4) = ?
2 × 20 = ?
2 × 20 = 40
L’associativité s’applique aussi à l’addition et à la multiplication de nombres décimaux.
Exemples :
| Addition | Multiplication |
|---|---|
| 3,45 + 2,7 + 9,12 = 15,27 (3,45 + 2,7) + 9,12 = 15,27 3,45 + (2,7 + 9,12) = 15,27 |
4,15 × 1,6 × 4,5 = 29,88 (4,15 × 1,6) × 4,5 = 29,88 4,15 × (1,6 × 4,5) = 29,88 |
La distributivité est une propriété de la multiplication. Elle permet à une multiplication d’être distribuée sur une addition ou une soustraction.
N’oublie pas que tu dois suivre la priorité des opérations dans une chaine d’opérations.
Pour en savoir plus, tu peux lire la fiche La priorité des opérations.
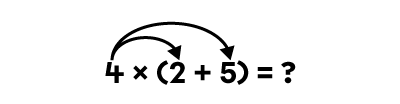
Lorsque j’effectue l’opération 4 × (2 + 5), j’obtiens 28.
4 × (2 + 5) = ?
4 × 7 = ?
4 × 7 = 28
Lorsque je distribue la multiplication sur l’addition, j’obtiens aussi 28.
|
(4 × 2) + (4 × 5) = ? |
 |
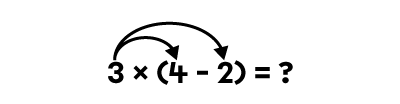
Lorsque j’effectue l’opération 3 × (4 - 2), j’obtiens 6.
3 × (4 - 2) = ?
3 × 2 = ?
3 × 2 = 6
Lorsque je distribue la multiplication sur la soustraction, j’obtiens aussi 6.
|
(3 × 4) - (3 × 2) = ? |
 |
La distributivité s’applique aussi sur des nombres décimaux.
Exemple :
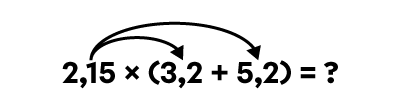
Lorsque j’effectue l’opération 2,15 × (3,2 + 5,2), j’obtiens 18,06.
2,15 × (3,2 + 5,2) = ?
2,15 × 8,4 = ?
2,15 × 8,4 = 18,06
Lorsque je distribue la multiplication sur l’addition, j’obtiens aussi 18,06.
|
(2,15 × 3,2) + (2,15 × 5,2) = ? |
 |