Afin de modéliser la fonction sinus, il faut connaitre le rôle des différents paramètres qui lui sont associés.
Par la suite, on peut procéder par étape afin de résoudre le problème.
Dans certaines villes, comme Niagara Falls ou Londres, une grande roue est installée afin d'offrir une vue panoramique aux touristes qui le désirent.
Pour grimper à l'intérieur d'un tel manège, une plateforme a été installée à une hauteur équivalente à la moitié de celle de la grande roue. Afin d'éviter toutes collisions avec les passants, le point le plus bas de la grande roue se situe à 5 m du sol. Une fois le sommet atteint, les usagers se retrouvent à une hauteur impressionnante de 131 m. Dès l'embarquement fait, la nacelle dans laquelle les usagers prennent place se dirige vers le bas.
Sachant que la vue devient particulièrement spectaculaire à partir de 120 m d'altitude et que la grande roue prend 32 minutes pour effectuer un tour complet, pendant combien de temps les touristes seront-ils impressionnés par le paysage?
-
Selon la règle de la fonction sinus, déterminer la valeur de |\boldsymbol{a}|
Selon le contexte, la hauteur maximale atteinte par la roue est de | 131\ \text{m}| et le point le plus bas se trouve à |5 \ \text{m}.| Ainsi, ||\vert a \vert = \dfrac{\text{max} - \text{min}}{2} = \dfrac{131 - 5}{2} = 63||Puisque le départ se fait en direction du sol, la valeur du paramètre |a| sera négative : |a = -63.|
-
Selon la règle de la fonction sinus, déterminer la valeur de |\boldsymbol{(h,k)}|
Puisqu'au départ l'embarquement se fait à la moitié de la hauteur, soit au milieu du cycle de la grande roue, alors : ||\begin{align}h & = 0 \\k & = 5 + 63 \\& = 68 \end{align}||Ainsi, |(h,k) = (0,68)|
-
Selon la règle de la fonction sinus, déterminer la valeur de |\boldsymbol{b}|
Par définition, |b = \dfrac{2 \pi}{\text{période}} = \dfrac{2 \pi}{32} = \dfrac{\pi}{16}.|
-
Créer et résoudre l'équation en lien avec la situation
Puisqu'on veut atteindre le sommet de la grande roue, on doit résoudre : ||\begin{align}f(x) & = -63 \sin \left(\frac{\pi}{16} (x-0)\right) + 68 \\120 & = -63 \sin \left(\frac{\pi}{16} x \right) + 68 \\52 & = -63 \sin \left(\frac{\pi}{16} x \right) \\-\frac{52}{63} & = \sin \left(\frac{\pi}{16} x \right)\\-0{,}971 & \approx \frac{\pi}{16} x \end{align}||
-
Interprétation de la 1re valeur de |\boldsymbol{x}| possible
Pour obtenir une première valeur positive, on peut ajouter |2 \pi | à la valeur trouvée étant donné que la période de la fonction sinus de base est de |2 \pi :| ||\begin{align}-0{,}971 &= -0{,}971 + 2 \pi \\&\approx 5{,}309 \\\\ \Rightarrow\ 5{,}309 &\approx \frac{\pi}{16} x_1 \\27{,}05 &\approx x_1 \end{align}||
-
Interprétation de la 2e valeur de |\boldsymbol{x}| possible
Selon les propriétés du cercle trigonométrique, il existe un 2e point sur celui-ci qui est à la même hauteur que le 1er. Pour le déterminer, on effectue ||\begin{align}\pi - 1^{\text{re}}\text{ valeur en radians} & = \pi - -0{,}971 \\& \approx 4{,}111 \end{align}||Finalement, on résout l'équation de nouveau avec cette nouvelle valeur : ||\begin{align} 4{,}111 & = \dfrac{\pi}{16} x_2 \\ 20{,}95 & \approx x_2 \end{align}||
-
Interprétation de la réponse
Ainsi, la vue sera particulièrement spectaculaire pendant environ |27{,}05 - 20{,}95 = 6{,}10\ \text{minutes}.|
Pour être en mesure de bien suivre la démarche de résolution proposée, la fiche portant sur la résolution d'équation et d'inéquation sinus peut être un outil fort intéressant.
La fonction sinus a été utilisée puisque le début du graphique de la situation se situait sur l'axe d'oscillation de la fonction.
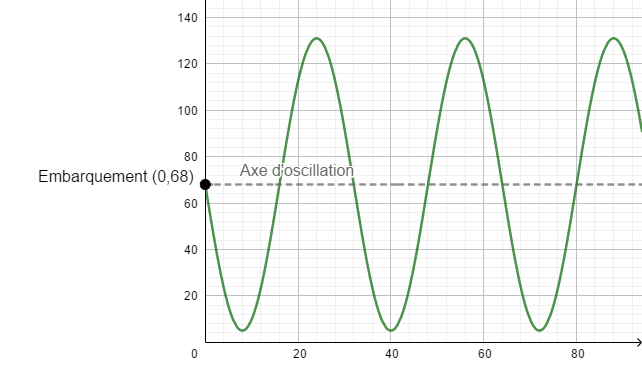
Si le point de départ avait fait référence à un maximum ou à un minimum, la fonction cosinus aurait été un choix plus judicieux.