Lorsqu’on veut calculer la probabilité d’un évènement d’une expérience aléatoire, il est nécessaire de dénombrer tous les résultats de l'univers des possibles.
Dans le cas d’une expérience aléatoire simple, il suffit d’écrire l’univers des possibles en extension et de compter le nombre d’éléments qu’il contient.
On lance un dé à |12| faces. L’univers des possible est représenté par l’ensemble |\Omega| suivant.||\Omega=\{1,2,3,4,5,6,7,8,9,10,11,12\}||Il y a |12| éléments dans |\Omega,| ce qui implique qu’il y a |12| résultats possibles dans cette expérience aléatoire.
Dans le cas d’une expérience aléatoire à plusieurs étapes, il faut d’abord vérifier si l’expérience tient compte ou non de l’ordre.
S’il s’agit d’une expérience aléatoire qui tient compte de l’ordre, on peut utiliser le principe multiplicatif. Cette méthode consiste à multiplier le nombre de choix à chaque étape de l’expérience pour connaitre le nombre de résultats possibles.
On lance une pièce de monnaie, puis on pige une bille dans un sac qui contient |3| billes rouges, |2| billes bleues et |4| billes vertes. Puisqu’il s’agit d’une expérience aléatoire à plusieurs étapes où on tient compte de l’ordre, on peut utiliser le principe multiplicatif pour connaitre le nombre de résultats possibles.
La 1re étape comporte |2| possibilités (pile ou face) et la 2e étape en contient |3| (bille rouge, bille bleue ou bille verte).||2\times3=6||Il y a donc |6| résultats possibles dans cette expérience aléatoire.
On peut calculer le nombre de résultats possibles d’une expérience aléatoire à plusieurs étapes à l’aide des permutations, des arrangements et des combinaisons.
Il existe plusieurs modes de représentation qui permettent de dénombrer les résultats possibles.
On peut organiser les résultats possibles d’une expérience aléatoire à 2 étapes à l’aide d’une grille.
Le nombre de résultats possibles correspond au nombre total de cases dans la grille. Pour le trouver, il suffit de faire le produit du nombre de lignes et du nombre de colonnes.
On fait tourner |2| roulettes. Les chiffres |1| à |4| représentent différentes sections de la 1re roulette, alors que les lettres |X,| |Y| et |Z| représentent les sections de la 2e roulette.
Quel est le nombre de résultats possibles dans cette expérience aléatoire?
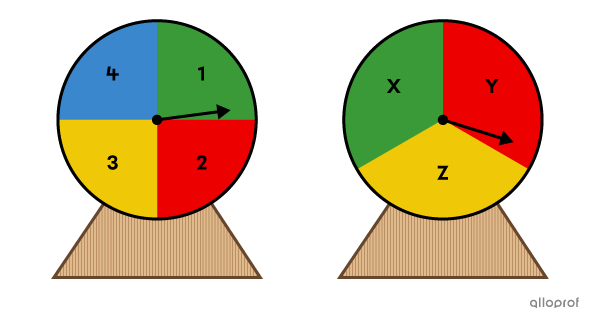
Cette situation est une expérience aléatoire composée, puisqu’elle comporte |2| étapes. On inscrit les choix possibles de la 1re roulette dans la 1re colonne du tableau et ceux de la 2e roulette dans la 1re ligne du tableau. Ensuite, on note les résultats possibles dans chaque case.
| |X| | |Y| | |Z| | |
|---|---|---|---|
| |1| | |(1,X)| | |(1,Y)| | |(1,Z)| |
| |2| | |(2,X)| | |(2,Y)| | |(2,Z)| |
| |3| | |(3,X)| | |(3,Y)| | |(3,Z)| |
| |4| | |(4,X)| | |(4,Y)| | |(4,Z)| |
Pour dénombrer les résultats possibles, il suffit de multiplier le nombre de lignes par le nombre de colonnes.||4\times3=12||Réponse : Il y a |12| résultats possibles dans cette expérience aléatoire.
On peut organiser les résultats possibles d’une expérience aléatoire à plusieurs étapes à l’aide d’un réseau.
Le nombre de résultats possibles correspond au nombre total de chemins qu’on peut emprunter dans le réseau. Pour le trouver, il suffit de faire le produit du nombre de branches à chaque étape.
Paul-Eugène se prépare pour aller dehors au printemps. Il choisit au hasard parmi les catégories de vêtements qu’il va porter dans cette liste.
-
Une tuque ou une casquette
-
Un manteau, un imperméable ou un chandail de laine
-
Des bottes, des souliers ou des sandales
Quel est le nombre de résultats possibles dans cette expérience aléatoire?
Cette situation est une expérience aléatoire composée, puisqu’elle comporte |3| étapes. On inscrit les possibilités pour chaque étape (catégorie) dans le réseau.
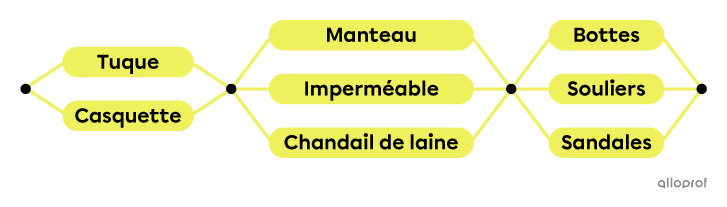
Pour dénombrer les résultats possibles, il suffit de multiplier le nombre de branches à chaque étape.||2\times3\times3=18||Réponse : Il y a |18| résultats possibles dans cette expérience aléatoire.
On peut organiser les résultats possibles d’une expérience aléatoire à plusieurs étapes à l’aide d’un schéma.
Le nombre de résultats possibles correspond au nombre total de liens dans le schéma. Pour le trouver, il suffit de les additionner tout en faisant attention de ne pas compter 2 fois le même lien.
Un groupe de |5| élèves participe à un concours de bras de fer. Chaque élève doit affronter une seule fois les autres élèves et celui qui gagne le plus de parties remporte le prix.
Quel est le nombre de joutes dans ce concours de bras de fer?
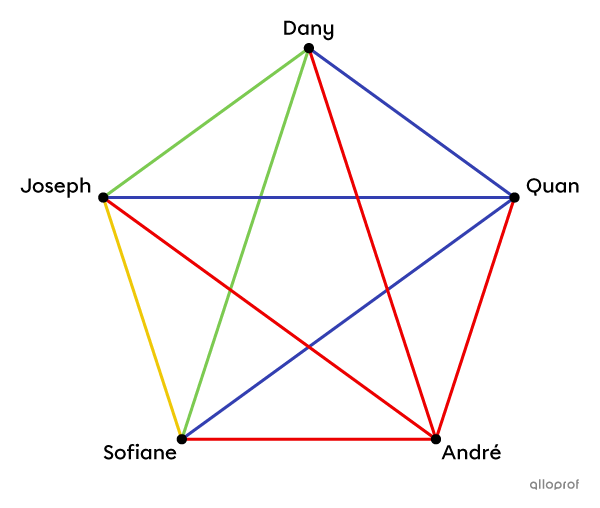
Pour dénombrer les résultats possibles, il suffit d’additionner le nombre de liens dans le schéma. On peut utiliser un système de couleurs afin de ne pas compter 2 fois le même lien. André affronte Quan, Dany, Joseph et Sofiane. Ensuite, Quan affronte les 3 autres adversaires, mais on ne compte pas une 2e fois son affrontement avec André. En appliquant le même raisonnement pour le reste des compétiteurs, on obtient le nombre de résultats possibles de la façon suivante.||\boldsymbol{\color{#ec0000}{4}}+\boldsymbol{\color{#333fb1}{3}}+\boldsymbol{\color{#7cca51}{2}}+\boldsymbol{\color{#efc807}{1}}=10||Réponse : Il y a |10| résultats possibles dans cette expérience aléatoire.
On peut organiser les résultats possibles d’une expérience aléatoire à plusieurs étapes à l’aide d’une diagramme sagittal.
Le nombre de résultats possibles correspond au nombre total de flèches dans le diagramme. Pour le trouver, il suffit de les compter ou de faire le produit du nombre d’éléments à chaque étape.
On veut déterminer le nombre de résultats possibles lorsqu’on pige une bille dans un sac contenant 3 billes de couleurs différentes (vert, orange, mauve) et qu’on lance ensuite une pièce de monnaie.
Quel est le nombre de résultats possibles dans cette expérience aléatoire?
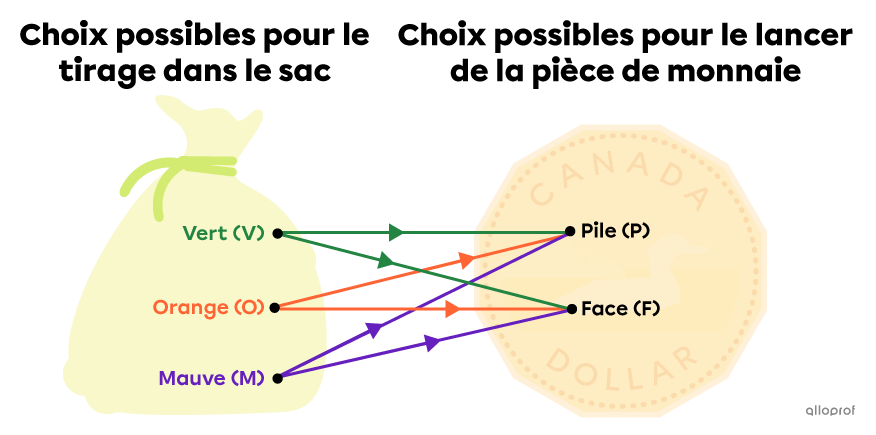
Pour dénombrer les résultats possibles, on peut multiplier le nombre d’éléments de la 1re étape |(3)| par le nombre d’éléments de la 2e étape |(2).|||3\times2=6||Réponse : Il y a |6| résultats possibles dans cette expérience aléatoire.