Lorsqu’on cherche à calculer une probabilité dans une expérience aléatoire à plusieurs étapes, il est nécessaire de dénombrer les résultats possibles.
Pour y arriver, il faut d’abord déterminer si l’expérience est avec ou sans ordre et avec ou sans remise. De plus, il faut vérifier si ce sont tous les éléments ou seulement certains des éléments de l’ensemble de départ qui sont pris en compte. Par la suite, on peut choisir la méthode appropriée parmi les suivantes.
Dispositions ordonnées de tous les éléments d’un ensemble
Dispositions ordonnées de certains des éléments d’un ensemble
Dispositions non ordonnées de certains des éléments d’un ensemble
Soit l’ensemble de départ |\{A,B,C\}.|
Les permutations de l’ensemble de départ sont les suivantes.||\begin{aligned}&(A,B,C)&&(A,C,B)\\&(B,A,C)&&(B,C,A)\\&(C,A,B)&&(C,B,A)\end{aligned}||Les arrangements de 2 éléments parmi les 3 de l’ensemble de départ sont les suivants.
Avec remise||\begin{aligned}&(A,A)&&(A,B)&&(A,C)\\&(B,A)&&(B,B)&&(B,C)\\&(C,A)&&(C,B)&&(C,C)\end{aligned}||
Sans remise||\begin{aligned}&&&(A,B)&&(A,C)\\&(B,A)&&&&(B,C)\\&(C,A)&&(C,B)&&\end{aligned}||
Les combinaisons de 2 éléments parmi les 3 de l’ensemble de départ sont les suivantes.
Avec remise||\begin{aligned}&(A,A)&&(A,B)&&(A,C)\\&&&(B,B)&&(B,C)\\&&&&&(C,C)\end{aligned}||
Sans remise||\begin{aligned}&&&(A,B)&&(A,C)\\&&&&&(B,C)\\&&&&&\end{aligned}||
Le diagramme en arbre est une bonne représentation visuelle pour mieux comprendre la logique derrière chacun de ces concepts.
Les permutations d'un ensemble d'éléments correspondent aux dispositions ordonnées de tous les éléments de cet ensemble.
Les permutations d'un ensemble se distinguent par l'ordre des éléments qui les composent. Par exemple, |(C,A,B)| et |(B,A,C)| sont 2 permutations différentes de |\{A,B,C\}.|
Autrement dit, les permutations de l’ensemble de départ d’une expérience aléatoire correspondent aux résultats de l’univers des possibles si cette expérience possède les caractéristiques suivantes.
-
L’expérience tient compte de l’ordre.
-
L’expérience est sans remise.
-
L’expérience implique tous les éléments de l’ensemble de départ.
Dans ce cas, on calcule les permutations de la façon suivante.
||\text{Nombre de permutations}=n\times(n-1)\times\ldots\times2\times 1||
où
|n :| nombre d’éléments dans l’ensemble de départ
On pige au hasard, sans remise et en tenant compte de l’ordre, toutes les billes d'un sac contenant une bille rouge |(R),| une bille bleue |(B),| une bille jaune |(J)| et une bille verte |(V).| Combien y a-t-il de résultats possibles?
On pourrait énumérer l’univers des possibles |(\Omega),| puis compter tous les éléments dans cet ensemble. Toutefois, on remarque que cette expérience aléatoire possède les 3 caractéristiques ci-dessous.
-
L’expérience tient compte de l’ordre.
-
L’expérience est sans remise.
-
L’expérience implique tous les éléments de l’ensemble de départ.
Il est donc plus efficace de calculer le nombre de résultats possibles en utilisant la formule du nombre de permutations de l’ensemble de départ |\{R,B,J,V\}.| Comme cet ensemble possède |4| éléments |(n=4),| on effectue le calcul suivant.||\begin{align}\text{Nombre de permutations}&=n\times(n-1)\times\ldots\times2\times 1\\&=4\times3\times2\times1\\&=24\end{align}||Réponse : Il y a |24| résultats possibles dans cette expérience aléatoire.
On peut représenter l’univers des possibles de l’exemple précédent à l’aide d’un diagramme en arbre.
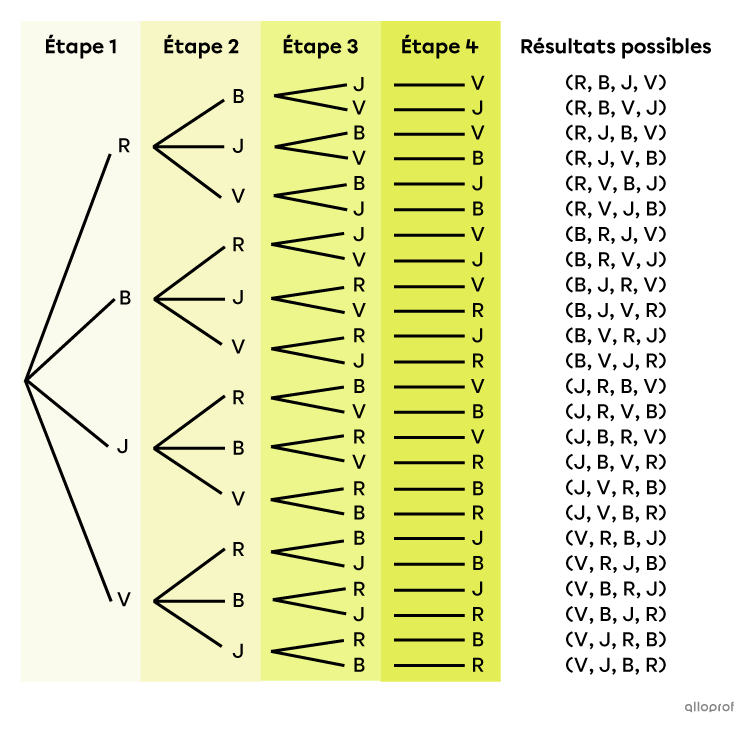
En analysant ce diagramme, on remarque qu’il y a 4 branches à la 1re étape, 3 branches à la 2e étape, 2 branches à la 3e étape et 1 branche à la 4e étape. Le nombre de branches diminue de 1 à chaque étape, car on ne remet jamais une bille dans le sac après l’avoir pigée. De plus, puisqu’on pige toutes les billes dans le sac, le nombre de branches diminue jusqu’à ce qu’il ne reste qu’un seul choix possible.
C’est la raison pour laquelle, selon le principe multiplicatif, on obtient la formule présentée plus haut.
On peut simplifier la formule du nombre de permutations à l’aide de la notation factorielle.||\text{Nombre de permutations}=n!||
où
|n :| nombre d’éléments dans l’ensemble de départ
Ainsi, dans l’exemple précédent, on aurait fait le calcul suivant.||\begin{align}\text{Nombre de permutations}&=n!\\&=4!\\&=4\times3\times2\times1\\&=24\end{align}||
Les arrangements d'un ensemble d'éléments correspondent aux dispositions ordonnées de certains éléments de cet ensemble.
Les arrangements d'un ensemble se distinguent par l'ordre des éléments qui les composent. Par exemple, |(A,C)| et |(C,A)| sont 2 arrangements différents de l’ensemble |\{A,B,C\}.|
Autrement dit, les arrangements de l’ensemble de départ d’une expérience aléatoire correspondent aux résultats de l’univers des possibles si cette expérience possède les caractéristiques suivantes.
-
L’expérience tient compte de l’ordre.
-
L’expérience est avec remise ou sans remise.
-
L’expérience implique certains des éléments parmi l’ensemble de départ.
Dans ce cas, on calcule les arrangements de la façon suivante.
Avec remise||\begin{gather}\text{Nombre d'arrangements}\\\text{avec remise}\end{gather}=n^k||
Sans remise||\begin{gather}\text{Nombre d'arrangements}\\\text{sans remise}\end{gather}=n\times(n-1)\times\ldots\times(n-k+1)||
où
|n :| nombre d’éléments dans l’ensemble de départ
|k :| nombre d’éléments sélectionnés dans l’ensemble de départ
Voici un exemple d’une expérience aléatoire avec remise.
On pige au hasard, avec remise et en tenant compte de l’ordre, 2 billes d'un sac contenant une bille rouge |(R),| une bille bleue |(B),| une bille jaune |(J)| et une bille verte |(V).| Combien y a-t-il de résultats possibles?
On pourrait énumérer l’univers des possibles |(\Omega),| puis compter tous les éléments dans cet ensemble. Toutefois, on remarque que cette expérience aléatoire possède les 3 caractéristiques ci-dessous.
-
L’expérience tient compte de l’ordre.
-
L’expérience est avec remise.
-
L’expérience implique certains des éléments parmi l’ensemble de départ.
Il est donc plus efficace de calculer le nombre de résultats possibles en utilisant la formule du nombre d’arrangements avec remise de l’ensemble de départ |\{R,B,J,V\}.| Comme cet ensemble possède |4| éléments |(n=4)| et qu’on en choisit |2| parmi ceux-ci |(k=2),| on effectue le calcul suivant.||\begin{aligned}\begin{gather}\text{Nombre d'arrangements}\\\text{avec remise}\end{gather}&=n^k\\&=4^2\\&=16\end{aligned}||Réponse : Il y a |16| résultats possibles dans cette expérience aléatoire.
On peut représenter l’univers des possibles de l’exemple précédent à l’aide d’un diagramme en arbre.
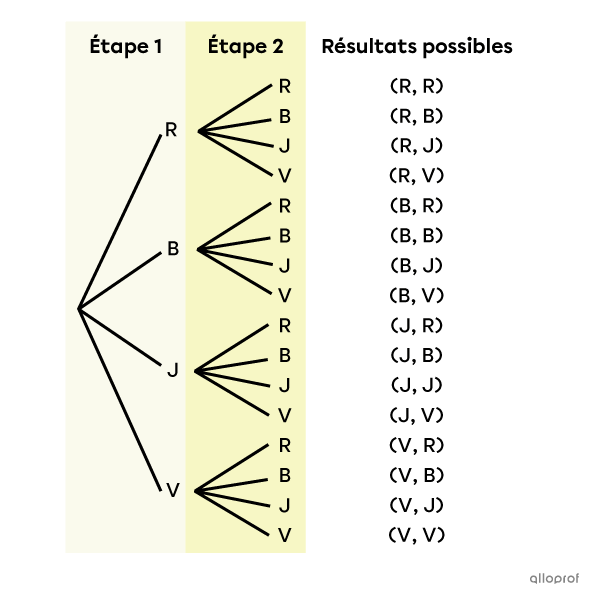
En analysant ce diagramme, on remarque qu’il y a 4 branches à la 1re étape et 4 branches à la 2e étape. Le nombre de branches ne diminue pas à chaque étape, car on remet toujours une bille dans le sac après l’avoir pigée.
C’est la raison pour laquelle, selon le principe multiplicatif et la notation exponentielle, on obtient la formule présentée plus haut.||\begin{aligned}\begin{gather}\text{Nombre d'arrangements}\\\text{avec remise}\end{gather}&=\underbrace{4\times 4}_{2\ \text{fois}}\\&=\underbrace{n\times n}_{k\ \text{fois}}\\&=n^k\end{aligned}||
Voici un exemple d’une expérience aléatoire sans remise.
On pige au hasard, sans remise et en tenant compte de l’ordre, 2 billes d'un sac contenant une bille rouge |(R),| une bille bleue |(B),| une bille jaune |(J)| et une bille verte |(V).| Combien y a-t-il de résultats possibles?
On pourrait énumérer l’univers des possibles |(\Omega),| puis compter tous les éléments dans cet ensemble. Toutefois, on remarque que cette expérience aléatoire possède les 3 caractéristiques ci-dessous.
-
L’expérience tient compte de l’ordre.
-
L’expérience est sans remise.
-
L’expérience implique certains des éléments parmi l’ensemble de départ.
Il est donc plus efficace de calculer le nombre de résultats possibles en utilisant la formule du nombre d’arrangements sans remise de l’ensemble de départ |\{R,B,J,V\}.| Comme cet ensemble possède |4| éléments |(n=4)| et qu’on en choisit |2| parmi ceux-ci |(k=2),| on effectue le calcul suivant, en commençant à |4| et en s’arrêtant à |n-k+1=4-2+1=3.|||\begin{aligned}\begin{gather}\text{Nombre d'arrangements}\\\text{sans remise}\end{gather}&=n\times(n-1)\times\ldots\times(n-k+1)\\&=4\times3\\&=12\end{aligned}||Réponse : Il y a |12| résultats possibles dans cette expérience aléatoire.
On peut représenter l’univers des possibles de l’exemple précédent à l’aide d’un diagramme en arbre.
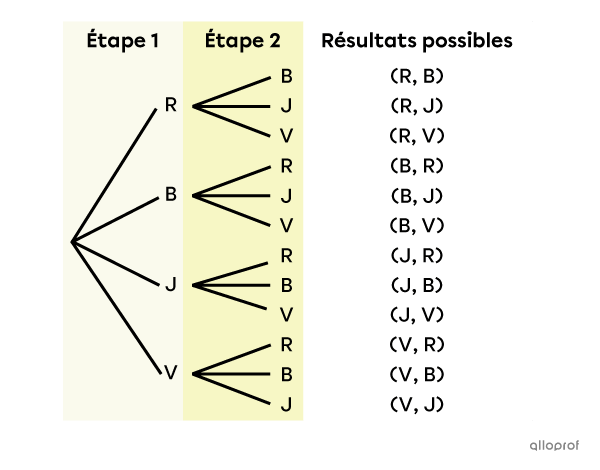
En analysant ce diagramme, on remarque qu’il y a 4 branches à la 1re étape et 3 branches à la 2e étape. Le nombre de branches diminue de 1 à chaque étape, car on ne remet jamais une bille dans le sac après l’avoir pigée. De plus, puisqu’on ne pige pas toutes les billes dans le sac, le nombre de branches diminue jusqu’à ce qu’on ait effectué toutes les étapes de l’expérience.
C’est la raison pour laquelle, selon le principe multiplicatif, on obtient la formule présentée plus haut.
On peut simplifier la formule du nombre d’arrangements sans remise à l’aide de la notation factorielle.||\begin{gather}\text{Nombre d'arrangements}\\\text{sans remise}\end{gather}=\dfrac{n!}{(n-k)!}||
où
|n :| nombre d’éléments dans l’ensemble de départ
|k :| nombre d’éléments sélectionnés dans l’ensemble de départ
Ainsi, dans l’exemple précédent, on aurait fait le calcul suivant.||\begin{aligned}\begin{gather}\text{Nombre d'arrangements}\\\text{sans remise}\end{gather}&=\dfrac{n!}{(n-k)!}\\&=\dfrac{4!}{(4-2)!}\\&=\dfrac{4!}{2!}\\&=\dfrac{4\times3\times2\times1}{2\times1}\\&=12\end{aligned}||
Les combinaisons d'un ensemble d'éléments correspondent aux dispositions non ordonnées de certains éléments de cet ensemble.
Les combinaisons d'un ensemble ne se distinguent pas par l'ordre des éléments qui les composent. Par exemple, |(A,C)| et |(C,A)| sont 2 combinaisons équivalentes de l’ensemble |\{A,B,C\}.|
Autrement dit, les combinaisons de l’ensemble de départ d’une expérience aléatoire correspondent aux résultats de l’univers des possibles si cette expérience possède les caractéristiques suivantes.
-
L’expérience ne tient pas compte de l’ordre.
-
L’expérience est avec remise ou sans remise.
-
L’expérience implique certains des éléments parmi l’ensemble de départ.
Dans le cas où l’expérience est sans remise, on calcule les combinaisons de la façon suivante.
||\begin{gather}\text{Nombre de combinaisons}\\\text{sans remise}\end{gather}=\dfrac{\begin{gather}\text{Nombre d'arrangements}\\\text{sans remise}\end{gather}}{\begin{gather}\text{Nombre de permutations}\\\text{des arrangements}\end{gather}}||
Le concept de combinaison fait appel aux permutations et aux arrangements. Cependant, on doit calculer les permutations des arrangements et non les permutations de l’ensemble de départ.
Autrement dit, pour calculer les permutations des arrangements, on doit utiliser la formule des permutations dans laquelle on utilise la valeur de |k| plutôt que la valeur de |n.|||\begin{gather}\text{Nombre de permutations}\\\text{des arrangements}\end{gather}=k\times(k-1)\times\ldots\times2\times1||
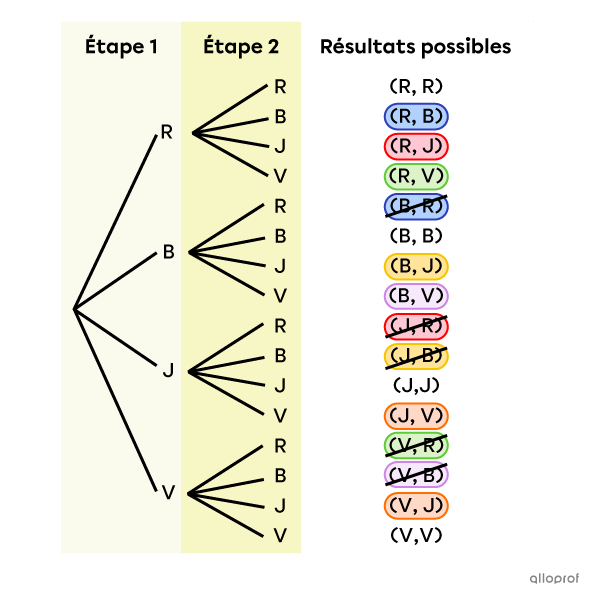
On pige au hasard, sans remise et sans tenir compte de l’ordre, 2 billes d’un sac contenant une bille rouge |(R),| une bille bleue |(B),| une bille jaune |(J)| et une bille verte |(V).| Combien y a-t-il de résultats possibles?
On pourrait énumérer l’univers des possibles |(\Omega),| éliminer les résultats qui sont équivalents, puis compter tous les éléments restants dans cet ensemble. Toutefois, on remarque que cette expérience aléatoire possède les 3 caractéristiques ci-dessous.
-
L’expérience ne tient pas compte de l’ordre.
-
L’expérience est sans remise.
-
L’expérience implique certains des éléments parmi l’ensemble de départ.
Il est donc plus efficace de calculer le nombre de résultats possibles en utilisant la formule du nombre de combinaisons sans remise.||\begin{gather}\text{Nombre de combinaisons}\\\text{sans remise}\end{gather}=\dfrac{\begin{gather}\text{Nombre d'arrangements}\\\text{sans remise}\end{gather}}{\begin{gather}\text{Nombre de permutations}\\\text{des arrangements}\end{gather}}||Puisque l’ensemble de départ |\{R,B,J,V\}| possède |4| éléments |(n=4)| et qu’on en choisit |2| parmi ceux-ci |(k=2),| on procède de la façon suivante.
On commence par calculer le nombre d’arrangements sans remise en arrêtant la multiplication à |n-k+1=4-2+1=3.|||\begin{aligned}\begin{gather}\text{Nombre d'arrangements}\\\text{sans remise}\end{gather}&=n\times(n-1)\times\ldots\times(n-k+1)\\&=4\times3\\&=12\end{aligned}||On calcule ensuite le nombre de permutations des arrangements. Attention! Ici, la valeur à utiliser est |2| et non |4.| En effet, puisqu’on s’intéresse aux permutations des arrangements et non aux permutations de l’ensemble de départ, on doit utiliser la valeur de |k| plutôt que la valeur de |n.|||\begin{aligned}\begin{gather}\text{Nombre de permutations}\\\text{des arrangements}\end{gather}&=k\times(k-1)\times\ldots\times2\times1\\&=2\times1\\&=2\end{aligned}||Finalement, on remplace ces 2 résultats dans la formule du nombre de combinaisons sans remise.||\begin{aligned}\begin{gather}\text{Nombre de combinaisons}\\\text{sans remise}\end{gather}&=\dfrac{\begin{gather}\text{Nombre d'arrangements}\\\text{sans remise}\end{gather}}{\begin{gather}\text{Nombre de permutations}\\\text{des arrangements}\end{gather}}\\&=\dfrac{12}{2}\\&=6\end{aligned}||Réponse : Il y a |6| résultats possibles dans cette expérience aléatoire.
On peut représenter l’univers des possibles de l’exemple précédent à l’aide d’un diagramme en arbre.
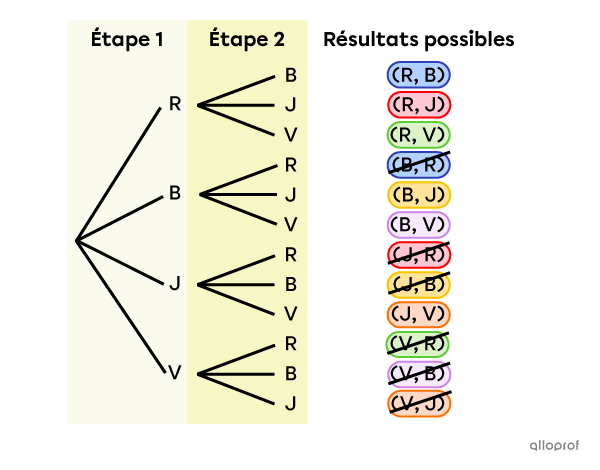
En analysant ce diagramme, on remarque qu’il y a 4 branches à la 1re étape et 3 branches à la 2e étape. Le nombre de branches diminue de 1 à chaque étape, car on ne remet jamais une bille dans le sac après l’avoir pigée. De plus, puisqu’on ne pige pas toutes les billes dans le sac, le nombre de branches diminue jusqu’à ce qu’on ait effectué toutes les étapes de l’expérience. Aussi, en observant les 12 résultats au bout des branches, on remarque qu’il y a des regroupements de 2 qui sont équivalents.
C’est pourquoi on doit diviser le nombre d’arrangements |(12)| par leur nombre de permutations |(2),| comme dans la formule présentée plus haut.
On peut simplifier la formule du nombre de combinaisons sans remise à l’aide de la notation factorielle.||\begin{gather}\text{Nombre de combinaisons}\\\text{sans remise}\end{gather}=\dfrac{n!}{k!(n-k)!}||
où
|n :| nombre d’éléments dans l’ensemble de départ
|k :| nombre d’éléments sélectionnés dans l’ensemble de départ
Ainsi, dans l’exemple précédent, on aurait fait le calcul suivant.||\begin{aligned}\begin{gather}\text{Nombre de combinaisons}\\\text{sans remise}\end{gather}&=\dfrac{n!}{k!(n-k)!}\\&=\dfrac{4!}{2!(4-2)!}\\&=\dfrac{4!}{2!\times2!}\\&=\dfrac{4\times3\times2\times1}{2\times1\times2\times1}\\&=6\end{aligned}||
Dans une expérience aléatoire à plusieurs étapes, avec remise et où on ne tient pas compte de l’ordre, le nombre de combinaisons de certains des éléments parmi l’ensemble de départ se calcule de la façon suivante.
||\begin{gather}\text{Nombre de combinaisons}\\\text{avec remise}\end{gather}=\dfrac{(n+k-1)!}{k!(n-1)!}||où
|n :| nombre d’éléments dans l’ensemble de départ
|k :| nombre d’éléments sélectionnés dans l’ensemble de départ
On pige au hasard, avec remise et sans tenir compte de l’ordre, 2 billes d’un sac contenant une bille rouge |(R),| une bille bleue |(B),| une bille jaune |(J)| et une bille verte |(V).| Combien y a-t-il de résultats possibles?
On pourrait énumérer l’univers des possibles |(\Omega),| éliminer les résultats qui sont équivalents, puis compter tous les éléments restants dans cet ensemble. Toutefois, on remarque que cette expérience aléatoire possède les 3 caractéristiques ci-dessous.
-
L’expérience ne tient pas compte de l’ordre.
-
L’expérience est avec remise.
-
L’expérience implique certains des éléments parmi l’ensemble de départ.
Il est donc plus efficace de calculer le nombre de résultats possibles en utilisant la formule du nombre de combinaisons avec remise de l’ensemble de départ |\{R,B,J,V\}.| Comme cet ensemble possède |4| éléments |(n=4)| et qu’on en choisie |2| parmi ceux-ci |(k=2),| on effectue le calcul suivant||\begin{aligned}\begin{gather}\text{Nombre de combinaisons}\\\text{avec remise}\end{gather}&=\dfrac{(n+k-1)!}{k!(n-1)!}\\&=\dfrac{(4+2-1)!}{2!(4-1)!}\\&=\dfrac{5!}{2!\times3!}\\&=\dfrac{5\times4\times3\times2\times1}{2\times1\times3\times2\times1}\\&=10\end{aligned}||Réponse : Il y a |10| résultats possibles dans cette expérience aléatoire.
On peut représenter l’univers des possibles de l’exemple précédent à l’aide d’un diagramme en arbre. Il suffit d’éliminer les résultats qui sont équivalents.