Le diagramme de Venn est une représentation visuelle de 2 ou de plusieurs ensembles de l’univers des possibles. Un point situé à l’intérieur d’une courbe fermée indique qu’il appartient à l’ensemble en question.
Le diagramme de Venn sert à représenter des ensembles de nombres, comme les nombres entiers, les nombres pairs, les multiples de 5, etc. Il peut aussi servir à représenter certaines caractéristiques d’une population, comme la couleur des cheveux, le sexe, etc.
Dans les diagrammes de Venn, on peut placer la liste de tous les éléments de l’univers des possibles dans les différents ensembles représentés. Toutefois, il arrive qu’on se contente plutôt d’inscrire le nombre d’éléments (ou le pourcentage des éléments) qui se retrouvent dans chaque ensemble.
On veut classer la liste des sports suivants à l’aide d’un diagramme de Venn selon 2 grandes catégories : les sports d’hiver et les sports d’équipe.
- Hockey
- Soccer
- Football
- Boxe
- Volleyball
- Ski alpin
- Patin de vitesse
- Athlétisme
- Natation
- Rugby
Si on inscrit tous les sports de la liste dans le diagramme, on obtient le résultat suivant.
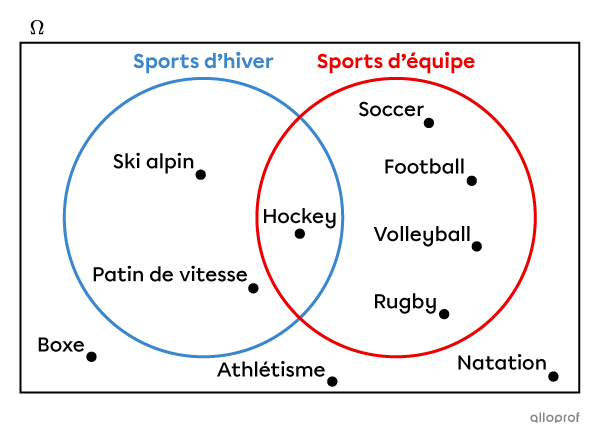
Si on inscrit seulement le nombre de sports dans chaque partie du diagramme, on obtient plutôt ce résultat.
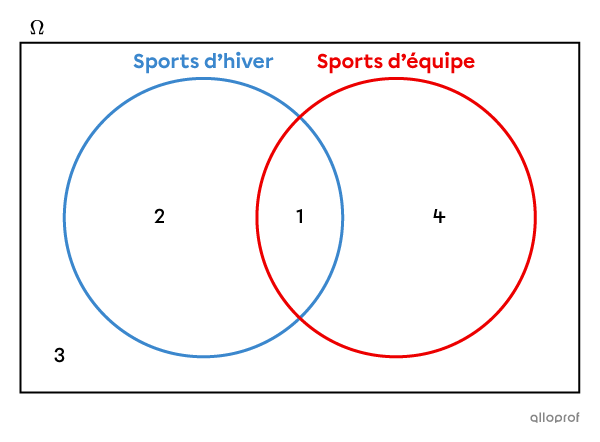
Lorsqu’il y a un très grand nombre d’éléments ou lorsqu’on ne possède pas la liste complète des éléments à classer, on utilise le 2e type de diagramme, soit celui où on inscrit simplement le nombre d’éléments.
Le diagramme suivant nous indique que 40 véhicules sur les 105 véhicules répertoriés ne sont ni un VUS ni un véhicule de couleur rouge. Il est préférable d’inscrire le nombre d’éléments présents dans chaque partie du graphique plutôt que d’y inscrire tous les éléments un par un.

On utilise un diagramme de Venn pour représenter des situations où on a 2 ou 3 ensembles.
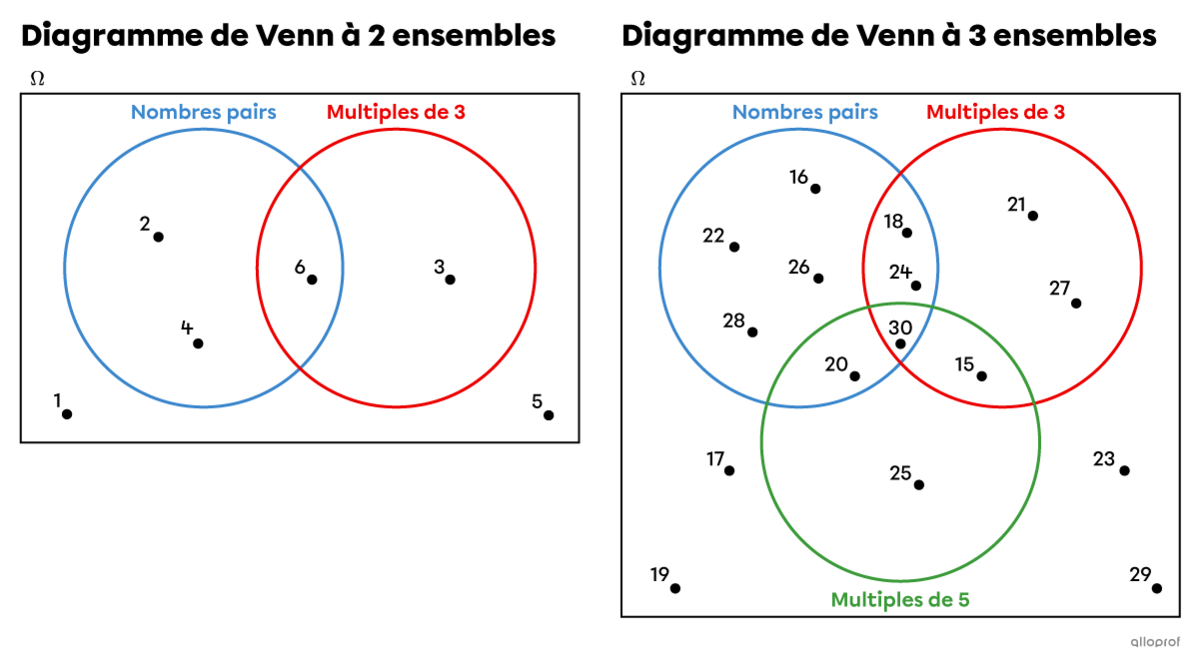
Lorsqu’on a plus de 3 ensembles, il devient très difficile d’utiliser un diagramme de Venn. Il est préférable d’utiliser un autre mode de représentation.
Un diagramme de Venn à 2 ensembles est formé de 4 zones distinctes : une qui est commune aux 2 ensembles, une exclusive à l’ensemble A, une exclusive à l’ensemble B et une qui représente le reste de l’univers des possibles.
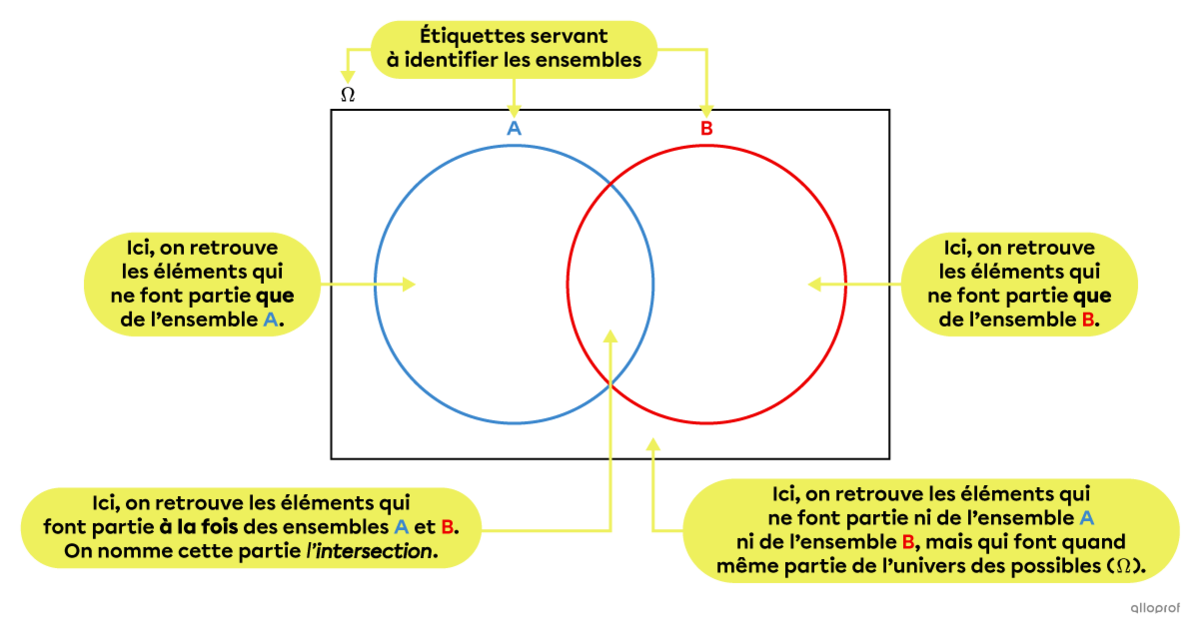
On nomme intersection de A et B la partie qui est commune aux 2 ensembles, tandis que l’union de A et B comprend tout ce qui est à l’intérieur de l’ensemble A ou de l’ensemble B, incluant la partie qui est commune à A et à B.
On associe souvent les notions d’union et d’intersection aux notions de « ou » et de « et » en probabilités.
Un diagramme de Venn à 3 ensembles est, quant à lui, formé de 8 zones distinctes.
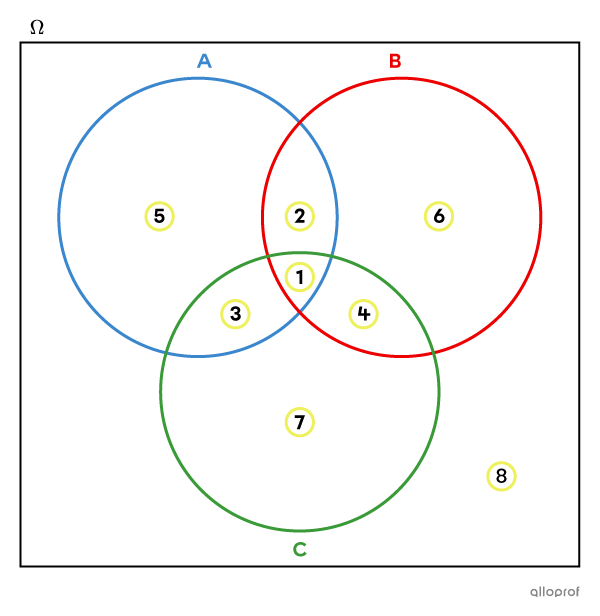
-
La zone 1 est commune aux 3 ensembles.
-
Les zones 2, 3 et 4 sont communes à 2 ensembles seulement.
-
Les zones 5, 6 et 7 sont exclusives à un seul ensemble.
-
La zone 8 ne fait partie d’aucun ensemble.
Après avoir interrogé de jeunes adultes de 24 ans pour savoir s’ils avaient un piercing ou un tatouage, on a représenté les résultats du sondage dans le diagramme de Venn suivant.
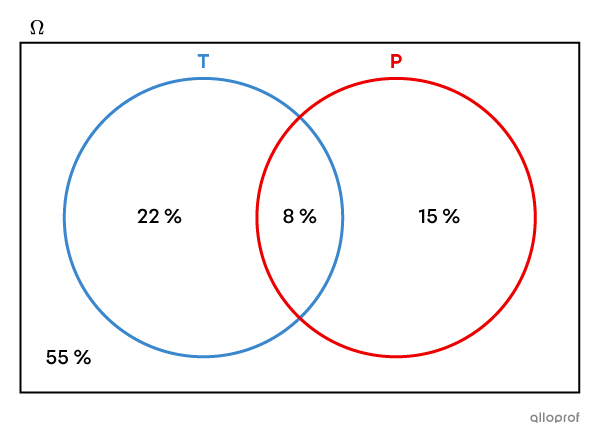
L’ensemble T représente les jeunes adultes qui ont (au moins) un tatouage.
L’ensemble P représente les jeunes adultes qui ont (au moins) un piercing (ailleurs qu’aux oreilles).
Voici les conclusions qu’on peut tirer directement du diagramme.
- |8\ \%| des jeunes adultes ont un tatouage et un piercing.
- |22\ \%| des jeunes adultes ont un tatouage, mais pas de piercing.
- |15\ \%| des jeunes adultes ont un piercing, mais pas de tatouage.
- |55\ \%| des jeunes adultes n’ont ni piercing ni tatouage.
Voici les conclusions supplémentaires qu’on peut tirer à l’aide de calculs simples.
- |22\ \%+8\ \%=30\ \%| des jeunes adultes ont un tatouage.
- |15\ \%+8\ \%=23\ \%| des jeunes adultes ont un piercing.
- |22\ \%+8\ \%+15\ \%= 45\ \%| des jeunes adultes ont un tatouage ou un piercing (ou les 2).
- |55\ \%+15\ \%=70\ \%| des jeunes adultes n’ont pas de tatouage.
- |55\ \%+22\ \%=77\ \%| des jeunes adultes n’ont pas de piercing.
Lorsqu’on remplit un diagramme de Venn, il est très important de s’assurer que la somme de tous les éléments placés correspond bien au nombre d’éléments dans l’univers des possibles, ni plus ni moins. Il faut donc porter une attention particulière aux expressions qu’on emploie, comme « un élément fait partie de A », « un élément fait partie de A, mais pas de B » ou encore « un élément ne fait partie que de A ».
Voici une procédure qui peut t’aider à remplir un diagramme de Venn.
-
Placer les éléments au centre du diagramme dans la partie commune à tous les ensembles, si possible.
-
Placer les éléments qui ne sont dans aucun ensemble, si possible.
-
Analyser chaque indice une première fois en plaçant les éléments dont on est certain, puis revenir sur les indices qui ont été laissés de côté.
-
S’assurer que tous les critères sont respectés, y compris le nombre total d’éléments de l’univers des possibles.
Dans le groupe 304, il y a 32 élèves, 12 parmi eux portent des lunettes et 7 élèves ont des broches. Finalement, 3 élèves ont à la fois des broches et des lunettes.
À l'aide d'un diagramme de Venn, détermine combien d’élèves ne portent pas de lunettes et n’ont pas de broches.
On commence par définir nos ensembles.
|\Omega :| tous les élèves du groupe 304
A : les élèves qui portent des lunettes
B : les élèves qui ont des broches
-
Placer les éléments communs
On inscrit |\color{#c58ae1}3| dans la partie qui est commune aux ensembles A et B. -
Compléter chacun des ensembles
On sait que |12| élèves portent des lunettes, mais on a déjà placé |\color{#c58ae1}3| personnes dans l’intersection des ensembles A et B. Ainsi, pour savoir combien d’élèves avec des lunettes il reste à placer, on fait |12-\color{#c58ae1}3,| ce qui donne |\color{#3b87cd}9.| On place donc |\color{#3b87cd}9| dans l’ensemble A, mais à l’extérieur de l’ensemble B.
On sait que |7| élèves ont des broches, mais on a déjà placé |\color{#c58ae1}3| personnes dans l’intersection des ensembles A et B. Ainsi, pour savoir combien d’élèves il reste à placer dans l’ensemble B, on fait |7-\color{#c58ae1}3,| ce qui donne |\color{#ec0000}4.| On place donc |\color{#ec0000}4| dans l’ensemble B, mais à l’extérieur de l’ensemble A. -
Placer les éléments qui ne sont dans aucun ensemble
Pour connaitre le nombre d’élèves restants, on soustrait les nombres déjà placés dans le diagramme |(\color{#3b87cd}9, \color{#c58ae1}3| et |\color{#ec0000}4)| du nombre total d’élèves dans la classe |(32).| ||32-\color{#3b87cd}9-\color{#c58ae1}3-\color{#ec0000}4=\color{#3a9a38}{16}||
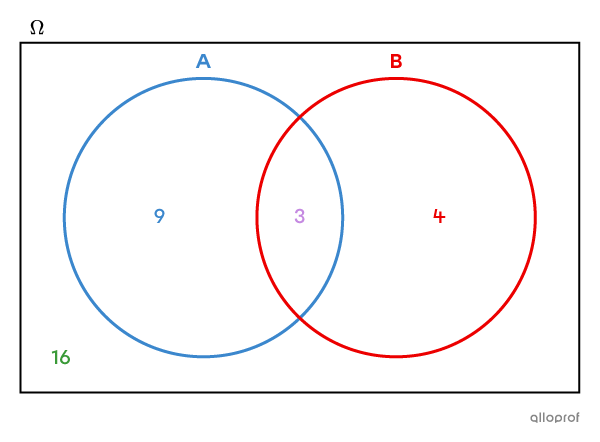
Réponse : Il y a |\color{#3a9a38}{16}| élèves dans le groupe 304 qui ne portent pas de lunettes et qui n’ont pas de broches.
Parmi les |164| élèves de 3e secondaire de l’école John Venn, on a fait une enquête pour savoir quels condiments (ketchup, relish ou moutarde) ils mettent dans leurs hotdogs.
Voici les résultats.
-
|10| élèves n’ajoutent aucun condiment.
-
|25| élèves ne mettent que du ketchup.
-
|27| élèves mettent de la relish et de la moutarde.
-
|15| élèves mettent les 3 condiments.
-
|70| élèves mettent 2 condiments.
-
|80| élèves mettent de la relish.
-
|19| élèves ne mettent que du ketchup et de la moutarde.
À l'aide d'un diagramme de Venn, détermine combien d’élèves mettent de la moutarde dans leurs hotdogs.
On commence par définir nos ensembles.
|\Omega :| tous les élèves de 3e secondaire de l’école John Venn.
K : les élèves qui mettent du ketchup dans leurs hotdogs
R : les élèves qui mettent de la relish
M : les élèves qui mettent de la moutarde
On analyse les indices un à la fois.
-
|10| élèves n’ajoutent aucun condiment.
Cela signifie que ces |10| élèves ne se retrouvent ni dans l’ensemble K, ni dans l’ensemble R, ni dans l’ensemble M. Il faut donc inscrire |10| dans l’univers des possibles, mais à l’extérieur des cercles.
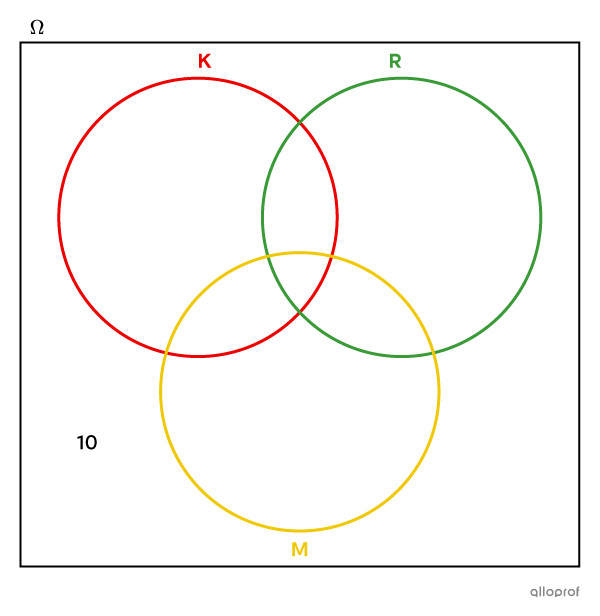
-
|25| élèves ne mettent que du ketchup.
On inscrit donc |25| dans la partie de l’ensemble K qui est à l’extérieur des ensembles R et M.
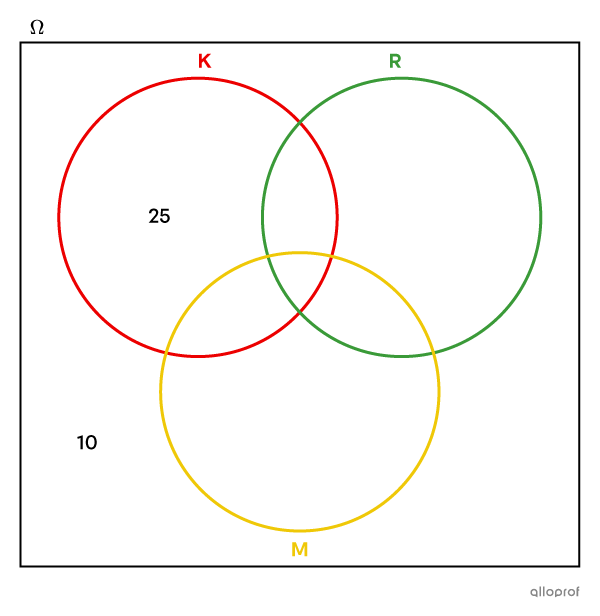
-
|27| élèves mettent de la relish et de la moutarde
Il y a donc un total de |27| élèves dans la partie commune aux ensembles R et M. Toutefois, cette partie du diagramme se divise elle-même en 2. Il faut donc analyser d’autres indices avant de répartir ces |27| élèves.
-
|15| élèves mettent les 3 condiments.
On inscrit donc |15| dans la partie commune aux 3 cercles.
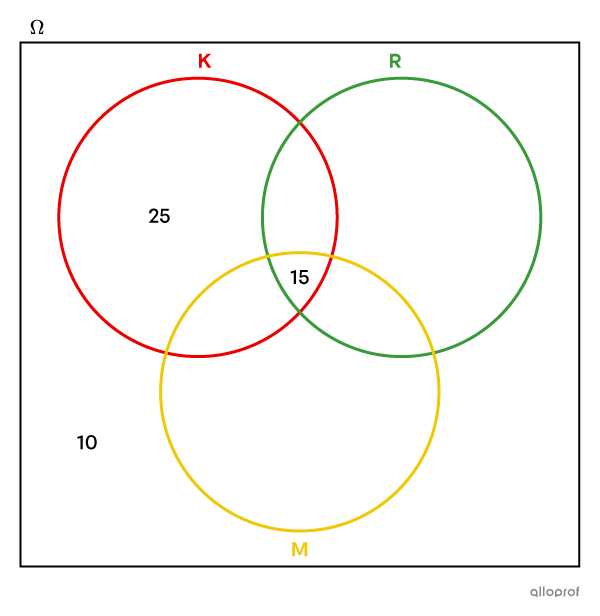
On revient à l’indice laissé de côté : |27| élèves mettent de la relish et de la moutarde.
On doit avoir un total de |27| dans la partie commune aux ensembles R et M. On en a déjà placé |15.| Il en reste donc |12| à placer, car |27-15=12.|
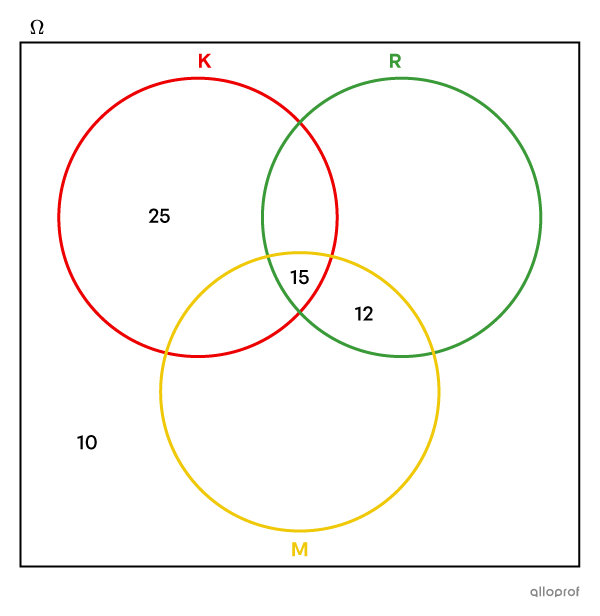
-
|70| élèves mettent 2 condiments.
Autrement dit, la somme des 3 sections qui sont communes à 2 ensembles doit être de |70.| On laisse cet indice de côté pour le moment.
-
|80| élèves mettent de la relish.
On doit aussi laisser cet indice de côté pour le moment, car il y a encore 2 parties de l’ensemble R à remplir.
-
|19| élèves ne mettent que du ketchup et de la moutarde.
Il faut donc placer |19| dans la partie commune aux ensembles K et M, mais à l’extérieur de R.

On revient au 1er indice laissé de côté : |70| élèves mettent 2 condiments.
On trouve le nombre à placer dans la partie commune aux ensembles K et R, mais à l’extérieure de M en faisant |70-19-12=39.|
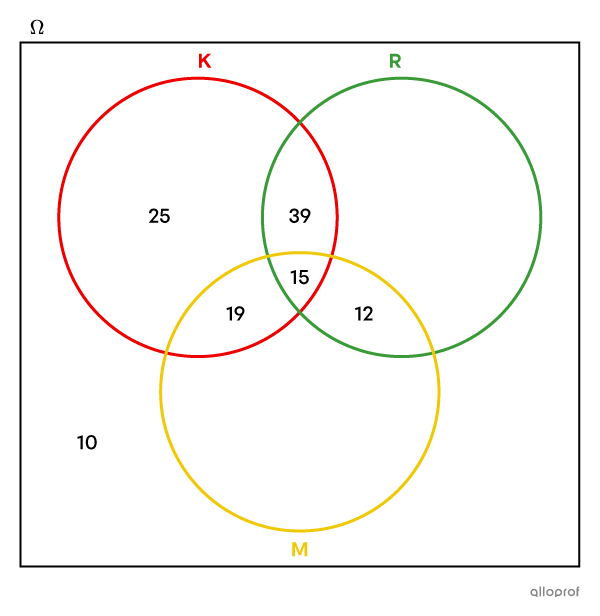
On revient au dernier indice laissé de côté : |80| élèves mettent de la relish.
On trouve maintenant le nombre d’élèves qui ne mettent que de la relish en faisant |80-39-15-12=14.|
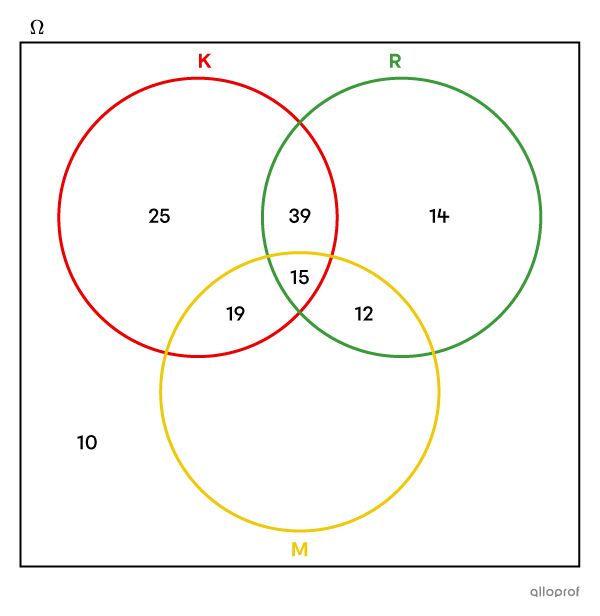
Toutes les parties du diagramme de Venn ont été remplies sauf une. Pour compléter le diagramme, il faut considérer le nombre total d’élèves interrogés : |164.| Ainsi, pour trouver la valeur à inscrire dans la section manquante, on fait une soustraction. ||164-25-39-14-10-19-15-12=30||

On peut maintenant répondre à la question. On sait que |30| élèves ne mettent que de la moutarde dans leurs hotdogs, mais si on veut connaitre le nombre total d’élèves qui mettent de la moutarde, il faut additionner les valeurs de toutes les parties de l’ensemble M. ||19+15+12+30=76||
Réponse : Il y a |76| élèves de 3e secondaire de l’école John Venn qui mettent de la moutarde dans leurs hotdogs.