Les expériences aléatoires avec ordre et sans ordre

On pige avec remise |2| billes dans un sac qui contient |3| billes bleues et |1| bille rouge.

Ce n’est pas toujours évident de savoir si une expérience aléatoire se fait avec ou sans ordre. Il faut toujours analyser le contexte pour le déduire.

Lorsqu’on analyse une expérience aléatoire à plusieurs étapes qui tient compte ou non de l’ordre, il faut aussi vérifier si elle se fait avec ou sans remise.

Une expérience aléatoire à plusieurs étapes où on tient compte de l’ordre est une expérience dans laquelle la séquence des résultats obtenus est importante.

Pascal pige |2| billes dans un sac qui contient |7| billes de couleurs. La 1^re bille qu’il pige est mauve et la 2^e est verte.

Si l’ordre dans lequel Pascal pige les billes est important, alors l’évènement « piger une bille mauve suivie d’une bille verte » n’est pas équivalent à l’évènement « piger une bille verte suivie d’une bille mauve ». 

Dans ce cas-ci, l’univers des possibles est représenté par l’ensemble suivant, qui contient plus de résultats possibles que dans le cas où on n’aurait pas tenu compte de l’ordre.||\Omega=\left\lbrace\begin{matrix}\begin{aligned}&(M,M)&&(M,B)&&(M,V)&&(M,O)\\&(B,M)&&(B,B)&&(B,V)&&(B,O)\\&(V,M)&&(V,B)&&(V,V)&&(V,O)\\&(O,M)&&(O,B)&&(O,V)&&(O,O)\end{aligned}\end{matrix}\right\rbrace||

Isabelle participe à un tirage où elle court la chance de gagner un ordinateur. Lors du tirage, Isabelle doit piger |3| cartons de couleurs dans un bocal opaque qui contient |3| cartons verts et |5| cartons rouges. Afin de gagner le tirage, Isabelle doit piger avec remise un carton vert, un carton rouge, puis un carton vert dans cet ordre précis.

Quelle est la probabilité qu’Isabelle remporte l’ordinateur?

Cette expérience aléatoire se fait avec remise, puisqu’Isabelle doit remettre le carton dans le bocal après chaque pige. Ainsi, le nombre total de cartons ne change pas d’une étape à l’autre. De plus, on doit tenir compte de l’ordre, puisque la séquence des cartons pigés est importante pour gagner l’ordinateur.

On commence par calculer la probabilité de chaque choix possible à la 1^re pige.||\begin{align}P(\text{vert})&=\dfrac{\text{Nombre de cartons verts}}{\text{Nombre total de cartons}}\\&=\dfrac{3}{8}\\\\P(\text{rouge})&=\dfrac{\text{Nombre de cartons rouges}}{\text{Nombre total de cartons}}\\&=\dfrac{5}{8}\end{align}||Puisque l’expérience se fait avec remise, les probabilités pour la 2^e et la 3^e pige restent les mêmes.

Ensuite, on calcule la probabilité associée à chaque résultat possible en multipliant la probabilité à chaque étape.||\begin{align}P(\text{vert, vert, vert})&=\dfrac{3}{8}\times\dfrac{3}{8}\times\dfrac{3}{8}=\dfrac{27}{512}\\P(\text{vert, vert, rouge})&=\dfrac{3}{8}\times\dfrac{3}{8}\times\dfrac{5}{8}=\dfrac{45}{512}\\P(\text{vert, rouge, rouge})&=\dfrac{3}{8}\times\dfrac{5}{8}\times\dfrac{5}{8}=\dfrac{75}{512}\\P(\text{rouge, rouge, rouge})&=\dfrac{5}{8}\times\dfrac{5}{8}\times\dfrac{5}{8}=\dfrac{125}{512}\end{align}||Pour s’aider à répondre à la question, on peut construire un diagramme en arbre.

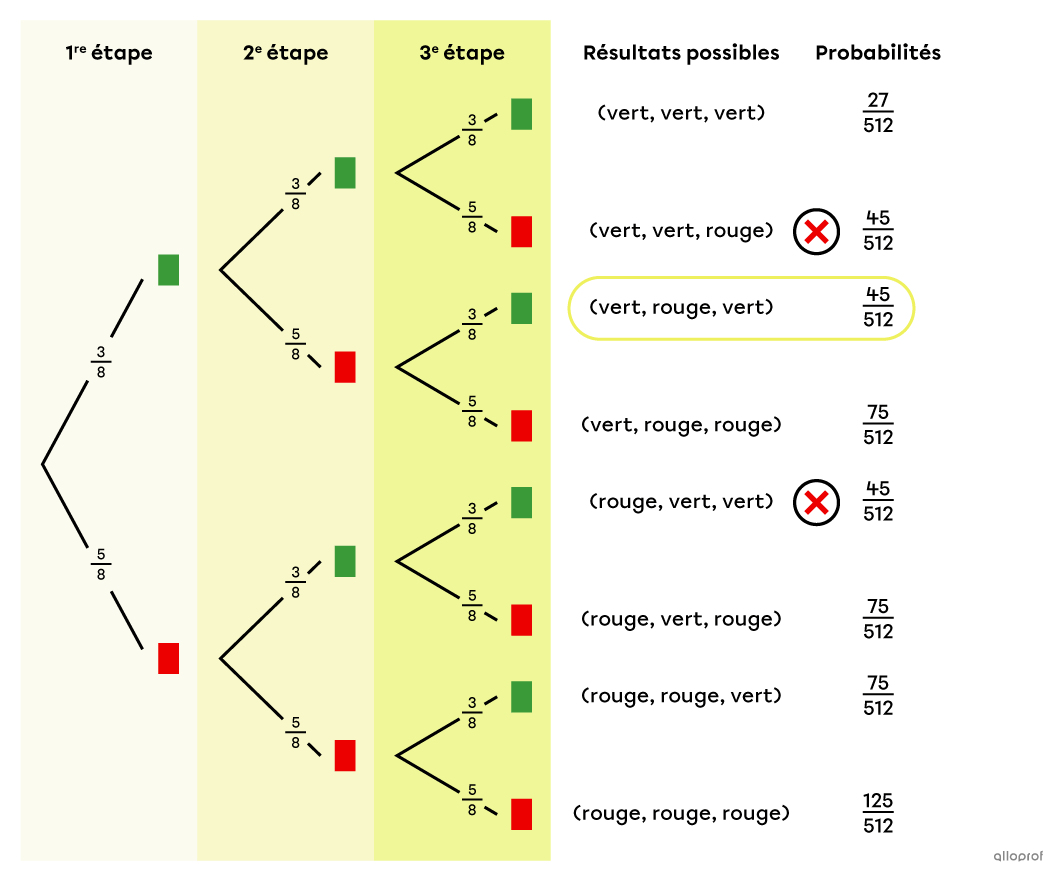
Le résultat possible qu’on cherche est |(\text{vert, rouge, vert}).| On ne considère pas les résultats |(\text{vert, vert, rouge})| et |(\text{rouge, vert, vert}),| puisqu’ils contiennent les bonnes couleurs, mais ne correspondent pas à la séquence précise qui permet à Isabelle de remporter le tirage.

Réponse : La probabilité qu’Isabelle remporte l’ordinateur est de |\dfrac{45}{512},| soit environ |9\ \%.|

​​​​​Lorsqu'on s'intéresse au nombre de résultats possibles d'une expérience aléatoire avec ordre, on peut aussi utiliser les formules d’arrangements.

Une expérience aléatoire à plusieurs étapes où on ne tient pas compte de l’ordre est une expérience dans laquelle la séquence des résultats obtenus n’est pas importante.

Pascal pige |2| billes dans un sac qui contient |7| billes de couleurs. La 1^re bille qu’il pige est mauve et la 2^e est verte.

Si l’ordre dans lequel Pascal pige les billes n’est pas important, alors l’évènement « piger une bille mauve suivie d’une bille verte » est équivalent à l’évènement « piger une bille verte suivie d’une bille mauve ». 

Dans ce cas-ci, l’univers des possibles est représenté par l’ensemble suivant, qui contient moins de résultats possibles que dans le cas où on aurait tenu compte de l’ordre.||\begin{align}\Omega&=\left\lbrace\begin{matrix}\begin{aligned}&(M,M)&&(M,B)&&(M,V)&&(M,O)\\&\cancel{(B,M)}&&(B,B)&&(B,V)&&(B,O)\\&\cancel{(V,M)}&&\cancel{(V,B)}&&(V,V)&&(V,O)\\&\cancel{(O,M)}&&\cancel{(O,B)}&&\cancel{(O,V)}&&(O,O)\end{aligned}\end{matrix}\right\rbrace\\\\&=\left\lbrace\begin{matrix}\begin{aligned}&(M,M)&&(M,B)&&(M,V)&&(M,O)\\&&&(B,B)&&(B,V)&&(B,O)\\&&&&&(V,V)&&(V,O)\\&&&&&&&(O,O)\end{aligned}\end{matrix}\right\rbrace
\end{align}||

Isabelle participe à un tirage où elle court la chance de gagner un ordinateur. Lors du tirage, Isabelle doit piger |3| cartons de couleurs dans un bocal opaque qui contient |3| cartons verts et |5| cartons rouges. Afin de gagner le tirage, Isabelle doit piger avec remise |2| cartons verts et |1| carton rouge.

Quelle est la probabilité qu’Isabelle remporte l’ordinateur?

Cette expérience aléatoire se fait avec remise, puisqu’Isabelle doit remettre le carton dans le bocal après chaque pige. Ainsi, le nombre total de cartons ne change pas d’une étape à l’autre. De plus, on ne doit pas tenir compte de l’ordre, puisque la séquence des cartons pigés n’est pas importante pour gagner l’ordinateur.

On commence par calculer la probabilité de chaque choix possible à la 1^re pige.||\begin{align}P(\text{vert})&=\dfrac{\text{Nombre de cartons verts}}{\text{Nombre total de cartons}}\\&=\dfrac{3}{8}\\\\P(\text{rouge})&=\dfrac{\text{Nombre de cartons rouges}}{\text{Nombre total de cartons}}\\&=\dfrac{5}{8}\end{align}||Puisque l’expérience se fait avec remise, les probabilités pour la 2^e et la 3^e pige restent les mêmes.

Ensuite, on calcule la probabilité associée à chaque résultat possible en multipliant la probabilité à chaque étape.||\begin{align}P(\text{vert, vert, vert})&=\dfrac{3}{8}\times\dfrac{3}{8}\times\dfrac{3}{8}=\dfrac{27}{512}\\P(\text{vert, vert, rouge})&=\dfrac{3}{8}\times\dfrac{3}{8}\times\dfrac{5}{8}=\dfrac{45}{512}\\P(\text{vert, rouge, rouge})&=\dfrac{3}{8}\times\dfrac{5}{8}\times\dfrac{5}{8}=\dfrac{75}{512}\\P(\text{rouge, rouge, rouge})&=\dfrac{5}{8}\times\dfrac{5}{8}\times\dfrac{5}{8}=\dfrac{125}{512}\end{align}||Pour s’aider à répondre à la question, on peut construire un diagramme en arbre.

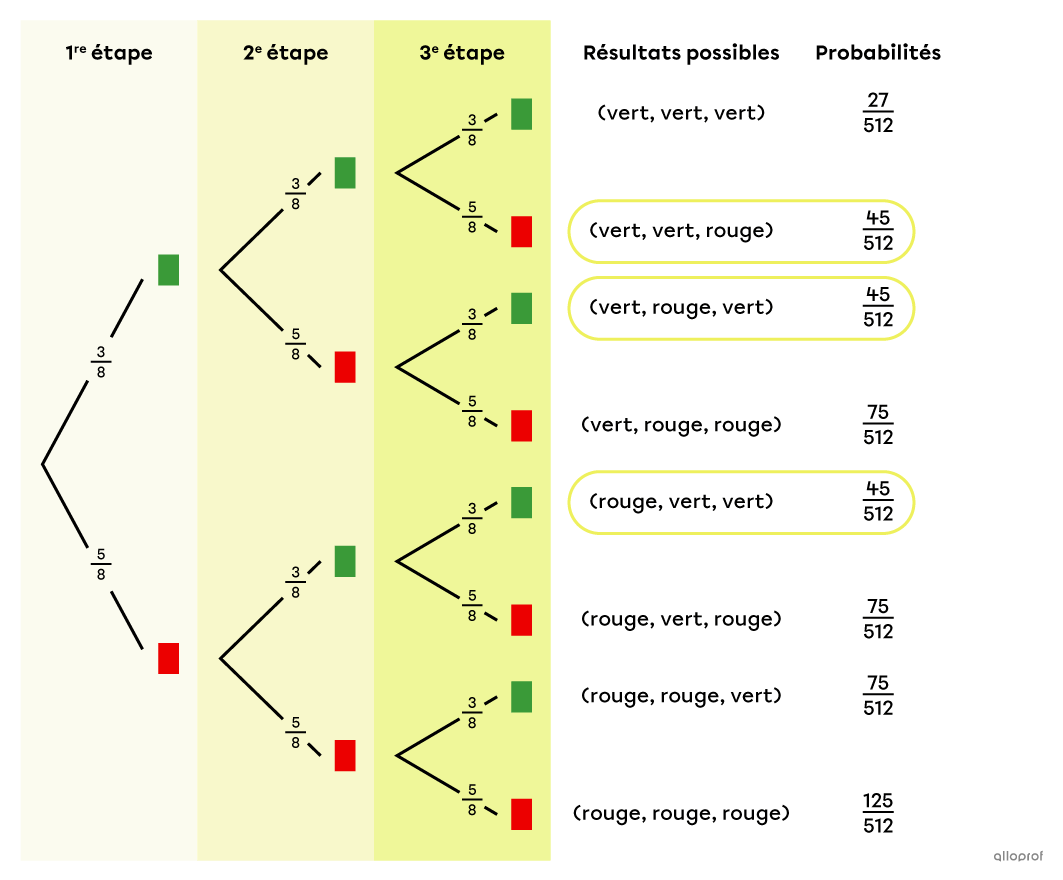
Les résultats favorables sont |(\text{vert, vert, rouge}),| |(\text{vert, rouge, vert})| et |(\text{rouge, vert, vert}),| puisqu’ils correspondent tous aux résultats qui permettent à Isabelle de remporter le tirage. Il ne reste donc qu’à additionner leur probabilité.||\begin{align}P(\text{2 verts et 1 rouge})&=\dfrac{45}{512}+\dfrac{45}{512}+\dfrac{45}{512}\\&=\dfrac{135}{512}\end{align}||Réponse : La probabilité qu’Isabelle remporte l’ordinateur est de |\dfrac{135}{512},| soit environ |26\ \%.|

Lorsqu'on s'intéresse au nombre de résultats possibles d'une expérience aléatoire sans ordre, on peut aussi utiliser les formules de combinaisons.

Lors de son anniversaire, Forrest se fait offrir par sa maman une boite contenant |10| chocolats. Elle sait que Forrest mangerait tous les chocolats d’un seul coup, alors sa maman lui suggère plutôt de fermer les yeux et d’en manger |3| au hasard. Dans la boite, il y a |4| chocolats noirs |(N),| |4| chocolats au lait |(L)| et |2| chocolats blancs |(B).|

Quelle est la probabilité que Forrest mange un chocolat de chaque type?

Cette expérience aléatoire se fait sans remise, puisque Forrest ne peut pas remettre les chocolats dans la boite après les avoir mangés. Ainsi, le nombre total de chocolats change d’une étape à l’autre. De plus, l’ordre dans lequel Forrest mange les chocolats n’est pas important, puisqu’on s’intéresse seulement au type des chocolats mangés par Forrest.

On commence par calculer la probabilité de chaque choix possible à la 1^re étape.||\begin{align}P(\text{N})&=\dfrac{\text{Nombre de chocolats noirs}}{\text{Nombre total de chocolats}}\\&=\dfrac{4}{10}\\\\P(\text{L})&=\dfrac{\text{Nombre de chocolats au lait}}{\text{Nombre total de chocolats}}\\&=\dfrac{4}{10}\\\\P(\text{B})&=\dfrac{\text{Nombre de chocolats blancs}}{\text{Nombre total de chocolats}}\\&=\dfrac{2}{10}\end{align}||Puisque l’expérience se fait sans remise, les probabilités changent à la 2^e étape. En effet, il y a |1| chocolat en moins dans la boite, ce qui implique que le dénominateur des fractions passe de |10| à |9| et que le numérateur diminue de |1| en fonction du résultat à la 1^re étape. Il en va de même à la 3^e étape.

Pour s’aider à répondre à la question, on peut construire un diagramme en arbre.

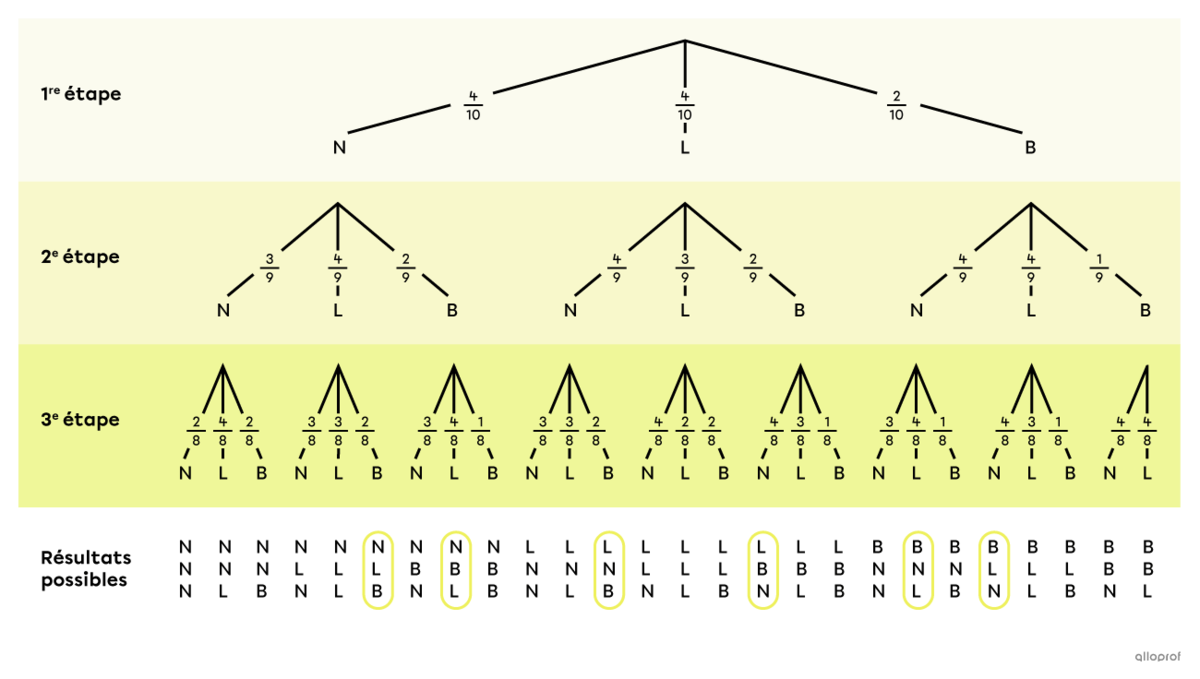
Ensuite, on identifie, dans le diagramme en arbre, les résultats possibles qui correspondent à l’évènement « manger un chocolat de chaque type ». Ces résultats possibles sont les suivants.||\begin{aligned}&(N,L,B)&&(N,B,L)\\&(L,N,B)&&(L,B,N)\\&(B,N,L)&&(B,L,N)\end{aligned}||On calcule d’abord les probabilités de chacun de ces résultats à l’aide du principe multiplicatif.||\begin{align}P(N,L,B)&=\dfrac{4}{10}\times\dfrac{4}{9}\times\dfrac{2}{8}=\dfrac{32}{720}\\P(N,B,L)&=\dfrac{4}{10}\times\dfrac{2}{9}\times\dfrac{4}{8}=\dfrac{32}{720}\\P(L,N,B)&=\dfrac{4}{10}\times\dfrac{4}{9}\times\dfrac{2}{8}=\dfrac{32}{720}\\P(L,B,N)&=\dfrac{4}{10}\times\dfrac{2}{9}\times\dfrac{4}{8}=\dfrac{32}{720}\\P(B,N,L)&=\dfrac{2}{10}\times\dfrac{4}{9}\times\dfrac{4}{8}=\dfrac{32}{720}\\P(B,L,N)&=\dfrac{2}{10}\times\dfrac{4}{9}\times\dfrac{4}{8}=\dfrac{32}{720}\\\end{align}||On additionne toutes les fractions ensemble.||\begin{align}P\left(\begin{gathered}\text{manger un chocolat}\\\text{de chaque type}\end{gathered}\right)&=\dfrac{32}{720}+\dfrac{32}{720}+\dfrac{32}{720}+\dfrac{32}{720}+\dfrac{32}{720}+\dfrac{32}{720}\\&=6\times\dfrac{32}{720}\\&=\dfrac{192}{720}\end{align}||Finalement, on réduit la fraction.||\begin{align}P\left(\begin{gathered}\text{manger un chocolat}\\\text{de chaque type}\end{gathered}\right)&=\dfrac{192\boldsymbol{\color{#ec0000}{\div48}}}{720\boldsymbol{\color{#ec0000}{\div48}}}\\&=\dfrac{4}{15}\end{align}||Réponse : La probabilité que Forrest mange au hasard un chocolat de chaque type est de |\dfrac{4}{15},| soit |26{,}\overline{6}\ \%.|