Les probabilités correspondent à la branche des mathématiques qui vise à mesurer le caractère aléatoire de ce qui pourrait se produire.
Calculer une probabilité revient donc à quantifier la possibilité qu'un évènement se produise lors d'une expérience qui découle du hasard. Cette probabilité varie selon l'évènement étudié et le type de probabilité recherché. Pour calculer des probabilités, il faut analyser des expériences aléatoires à une ou plusieurs étapes afin de faire le dénombrement de tous les résultats de l’univers des possibles. De plus, pour différents jeux de hasard, on peut déterminer les chances de gains ou de pertes et calculer ce qu’on peut espérer gagner ou perdre.
-
Une expérience aléatoire est une expérience dont le résultat dépend entièrement du hasard et dont les résultats possibles sont connus.
-
L’univers des possibles |\boldsymbol{(\Omega)}| est l’ensemble qui comprend tous les résultats possibles d’une expérience aléatoire.
-
Un évènement est un sous-ensemble de l’univers des possibles d’une expérience aléatoire.
-
Une probabilité est une valeur comprise entre |0| et |1| |(0\ \%| et |100\ \%)| qui quantifie la possibilité d’obtenir un résultat précis parmi tous les résultats possibles.
Un évènement peut correspondre à un seul résultat, à plusieurs résultats ou à la totalité des résultats de l'univers des possibles. Il peut aussi ne correspondre à aucun résultat.
Pour un évènement, une probabilité est égale au rapport entre le nombre de résultats favorables et le nombre de résultats possibles de l'expérience aléatoire.
||\text{Probabilité}=\dfrac{\text{Nombre de résultats favorables}}{\text{Nombre de résultats possibles}}||
Le lancer d’un dé à |6| faces est une expérience aléatoire, car tous les résultats possibles sont connus d’avance et ne dépendent que du hasard.
L’univers des possibles de cette expérience est |\Omega=\{1, 2, 3, 4, 5, 6\}.|
L’évènement |A| « obtenir un multiple de 3 » correspond à un sous-ensemble de l’univers des possibles. ||A=\{3,6\}||
On peut calculer la probabilité de l’évènement |A| en faisant le rapport entre le nombre d’éléments dans l’ensemble |A| et dans l’ensemble |\Omega.| ||P(A)=\dfrac{2}{6}=\dfrac{1}{3}||
Une expérience aléatoire peut se faire en une seule étape (expérience aléatoire simple) ou en plusieurs étapes (expérience aléatoire composée).
Il est utile de s’aider de différents modes de représentation (diagramme en arbre, diagramme de Venn, etc.) ainsi que du principe de multiplication pour faire le dénombrement de tous les résultats d’une expérience aléatoire.
Si une expérience aléatoire est composée de plusieurs étapes, l’univers des résultats possibles s’écrit en plaçant entre parenthèses les résultats obtenus à chaque étape.
On lance 2 pièces de monnaie et on s’intéresse aux résultats possibles.
Il s'agit d'une expérience aléatoire à 2 étapes.
L’univers des possibles est le suivant. ||\Omega =\{(\text{P},\text{P}), (\text{P},\text{F}), (\text{F},\text{P}), (\text{F},\text{F})\}||
où
|\text{P}:| Pile
|\text{F}:| Face
L’évènement |B| « obtenir au moins un côté face » est un sous-ensemble de |\Omega.| ||B=\{((\text{P},\text{F}), (\text{F},\text{P}), (\text{F},\text{F})\}||
On dénombre |3| résultats favorables à l’évènement |B| et |4| résultats possibles dans l’ensemble |\Omega.|
Ainsi, la probabilité d’obtenir au moins un côté face est la suivante.||P(B)=\dfrac{\text{Nombre de résultats favorables}}{\text{Nombre de résultats possibles}}=\dfrac{3}{4}||
Les jeux de hasard sont des expériences aléatoires. Il en existe plusieurs. En voici quelques exemples qui reviennent souvent pour étudier les probabilités.
Un jeu de cartes traditionnel sert à jouer à de nombreux jeux tels que le poker, le blackjack, la bataille, le solitaire, la dame de pique, le 8, le 9, le 500, etc.
Voici les particularités d’un jeu de 52 cartes.
Il y a 4 sortes : cœur et carreau qui sont en rouge, ainsi que pique et trèfle qui sont en noir.
Chaque sorte est composée de 13 cartes.
-
L’as (A)
-
Les cartes numérotées de 2 à 10
-
Les figures : le valet (V), la dame (D) et le roi (R)
Autrement dit, chaque jeu de cartes contient 4 valets, 4 dames, 4 rois et 4 as. C’est la même chose pour les cartes numérotées. Les valets, les dames et les rois forment ce qu’on appelle les figures. Dans un jeu de 52 cartes, il y a donc 12 figures en tout.
Remarque : Au Québec, on retrouve souvent des jeux de cartes anglophones. Au lieu de V, D et R pour Valet, Dame et Roi, on voit plutôt J, Q et K pour Jack, Queen et King.
Voici un tableau qui résume l’ensemble des cartes.
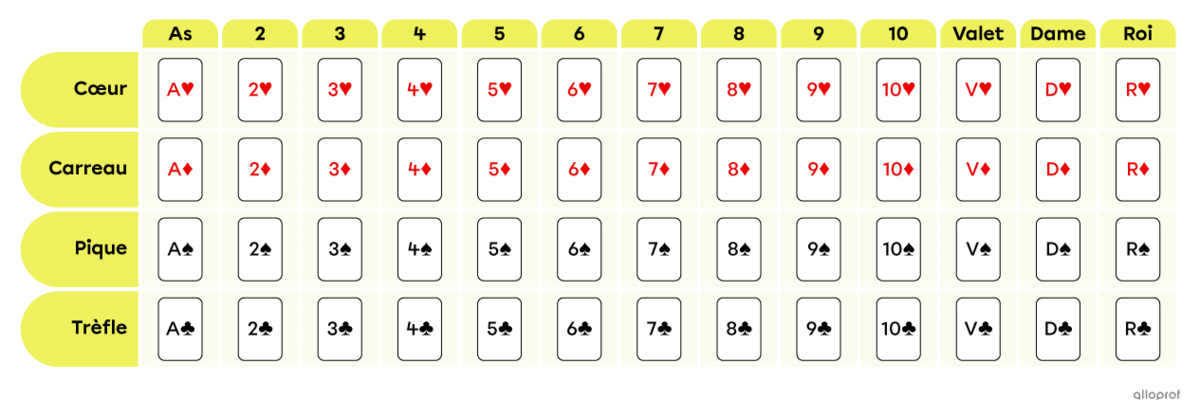
Remarque : Il est parfois question d’un jeu de 54 cartes. Il s’agit du même jeu de cartes auquel 2 cartes sont ajoutées : les jokers. Ceux-ci ne font partie d’aucune sorte. À moins d’indication contraire, dans les questions de probabilités, il ne faut pas tenir compte des jokers.

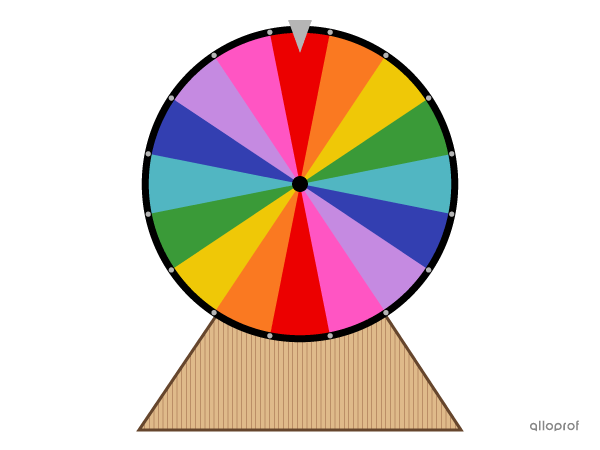
Il existe plusieurs jeux de hasard basés sur une roulette.
À la télévision, on voit souvent une roulette placée à la verticale qu’on appelle une roue chanceuse. Il suffit de faire tourner la roue. Lorsqu’elle s’arrête de tourner, on observe vers quel secteur du disque pointe la petite flèche et on gagne le prix qui y est indiqué.
Dans les casinos, on joue avec une roulette placée à plat sur la table. Un joueur peut miser sur un ou plusieurs nombres, sur une couleur, etc. On fait ensuite tourner la roulette en y plaçant une bille. Lorsqu’elle s’immobilise, le casino paye tous ceux qui ont fait des mises gagnantes selon le principe suivant : plus la probabilité de réalisation de l’évènement sur lequel on mise est petite, plus les gains sont grands.
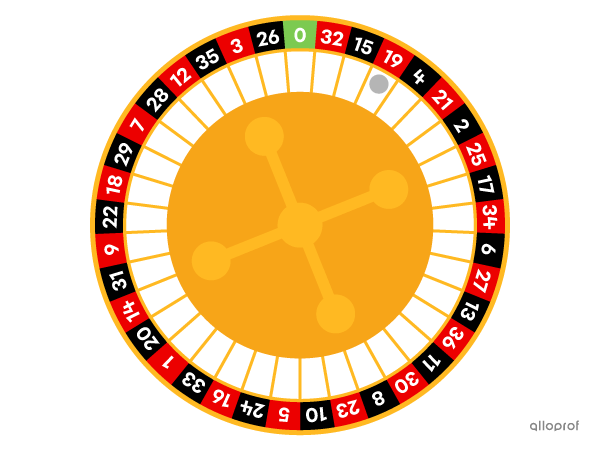
Remarque : La plupart des roulettes sont formées de secteurs de disque identiques, ce qui fait en sorte que la probabilité de chaque secteur est la même. Parfois, les secteurs ne sont pas identiques et il faut donc porter attention à l’angle au centre de chacun.
Il existe plusieurs sortes de dés. Il y a des dés à 4, 6, 8, 10, 12 et 20 faces.
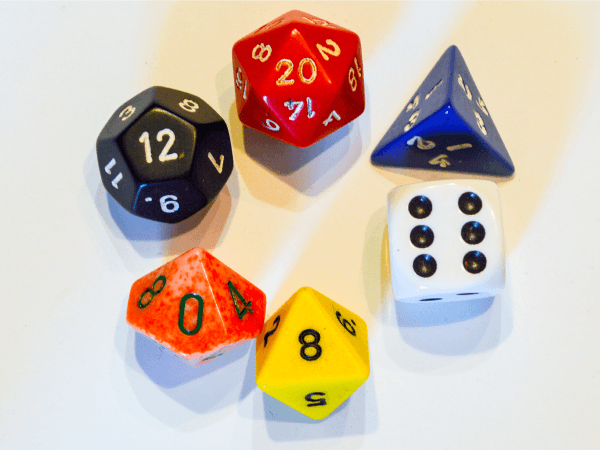
Marcovaldo, Shutterstock.com
Dans un problème donné, si ce n’est pas précisé, on peut tenir pour acquis qu’il s’agit d’un dé règlementaire à 6 faces. Un dé à 6 faces est règlementaire si la somme de 2 faces opposées donne toujours 7. Autrement dit, le 1 et le 6 sont sur des faces opposées. Il en est de même pour le couple (2, 5) et pour le couple (3, 4).
Un dé peut aussi être pipé, c’est-à-dire truqué. Il est truqué si ses faces ne sont pas réparties de la façon règlementaire ou si la masse du dé n’est pas répartie de façon uniforme. Par exemple, si le dé est plus lourd du côté du 1, le dé aura tendance à s’immobiliser plus souvent sur cette face que sur les autres faces.
Plusieurs expériences aléatoires sont en fait des tirages au sort. En voici quelques exemples.
-
Le tirage d’un prix de participation
-
Le bingo : on tire des boules d’un boulier jusqu’à ce qu’il y ait un gagnant. C’est une expérience aléatoire à plusieurs étapes.
-
Les loteries traditionnelles : il s’agit d’une expérience aléatoire à plusieurs étapes. Par exemple, pour la loterie 6-49, on tire 6 boules d’un boulier qui en contient 49.
-
Etc.
Une variable aléatoire quantitative est une variable qui peut prendre différentes valeurs dans une expérience aléatoire.
Soit la variable aléatoire |X| qui peut prendre des valeurs allant de |x_1| à |x_n.| Il s’agit, par exemple, des différents résultats d’une expérience aléatoire. Chacune de ces valeurs peut être associée à une probabilité. Ainsi, on peut représenter la distribution des probabilités de la variable aléatoire |X| de la façon suivante.
| |X| | |x_1| | |x_2| | |x_3| | ... | |x_n| |
|---|---|---|---|---|---|
| |P(X)| | |p(x_1)| | |p(x_2)| | |p(x_3)| | ... | |p(x_n)| |
Selon la génétique, la probabilité qu’une femme enceinte accouche d’un garçon (G) est pratiquement égale à celle qu’elle accouche d’une fille (F). Il s’agit donc d’une expérience aléatoire à une ou à plusieurs étapes si une femme a un ou plusieurs enfants. Pour ce qui est des familles de |3| enfants, la probabilité d’avoir |2| garçons est-elle la même que celle d’en avoir |3|?
On commence par énumérer toutes les familles de |3| enfants possibles. Il y en a |8| en tout.
FFF, FFG, FGF, FGG,
GFF, GFG, GGF, GGG
On observe ceci :
-
Il y a |1| des |8| modèles familiaux où il n’y a aucun garçon.
-
Il y a |3| cas sur |8| où il y a |\boldsymbol{\color{#ec0000}1}| garçon.
-
Il y a |3| cas sur 8 où il y a |\boldsymbol{\color{#560fa5}2}| garçons.
-
Il y a |1| cas sur 8 où il y a |\boldsymbol{\color{#333fb1}3}| garçons.
Ensuite, on définit la variable aléatoire |X| comme étant le nombre de garçons parmi les |3| enfants d’une famille.
Finalement, on représente ces résultats dans le tableau suivant.
| |X:| Nombre de garçons | |\boldsymbol{\color{#ff55c3}0}| | |\boldsymbol{\color{#ec0000}1}| | |\boldsymbol{\color{#560fa5}2}| | |\boldsymbol{\color{#333fb1}3}| |
|---|---|---|---|---|
| |P(X)| | |\ \dfrac{1}{8}\ | | |\ \dfrac{3}{8}\ | | |\ \dfrac{3}{8}\ | | |\ \dfrac{1}{8}\ | |
Réponse : La représentation des résultats à l’aide d’une variable aléatoire nous permet d’affirmer que la probabilité d’avoir |2| garçons sur |3| enfants n’est pas la même que celle d’en avoir |3.|
La représentation des résultats d’une expérience aléatoire et de leur probabilité à l’aide d’une variable aléatoire permet de calculer l’espérance mathématique de l’expérience en question.