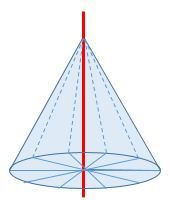
Le développement d'un cône est obtenu lorsque ses deux faces sont dessinées sur une feuille, donc sur le même plan.
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
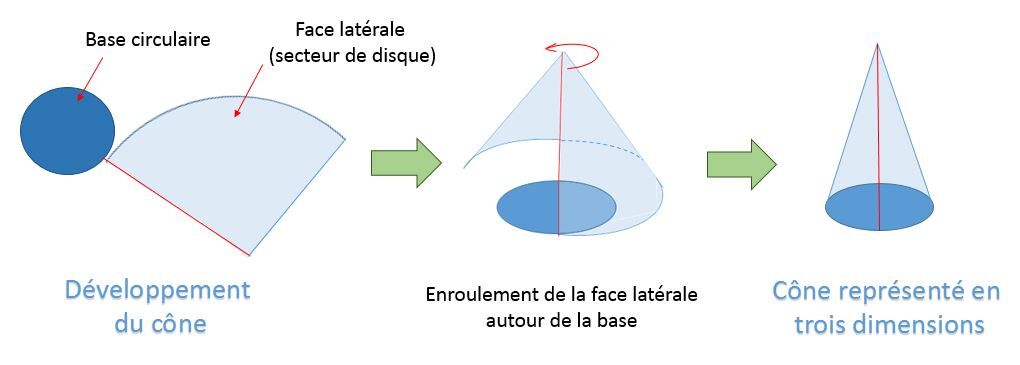
<html><body><p>Le <strong>développement d'un cône</strong> est une représentation en deux dimensions dont la base est un <a href="/fr/eleves/bv/mathematiques/les-cercles-et-les-disques-m1202#disque">disque</a> et la face latérale est un <a href="/fr/eleves/bv/mathematiques/les-cercles-et-les-disques-m1202#secteur-circulaire">secteur de disque</a>.<br>
<br>
Par ailleurs, on parlera de <strong>cône droit</strong> lorsque le sommet du cône (apex) est aligné avec le centre de la base.</p>
</body></html>
Le cône est un corps rond classé parmi les solides qui possède une seule base (un disque) et une face latérale (un secteur de disque).
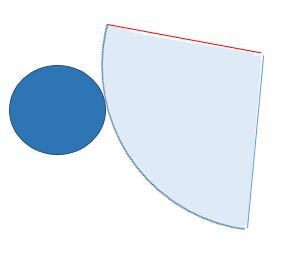
Il est à noter que, dans l'exemple précédent, la face latérale (secteur de disque) est collée au cercle par son extrémité ce qui facilite la visualisation de son enroulement autour de la base. Par contre, le développement du cône peut se faire de manière à ce que la portion courbe de cette face latérale touche au cercle à n'importe quel endroit.
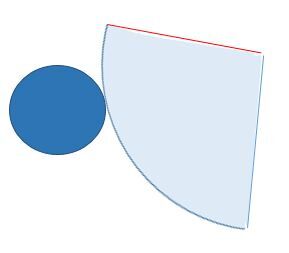
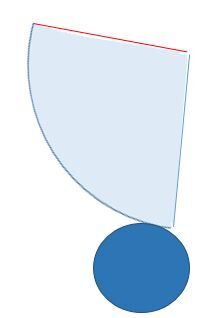
Pour que la face latérale s'enroule correctement autour de la base circulaire, il faut que l'arc de cercle du secteur de disque soit de la même longueur que la circonférence du cercle qui sert de base.
Par ailleurs, la mesure de l'angle au centre du secteur du disque est intimement liée à la circonférence de la base : plus la mesure de l'angle augmente, plus la mesure de la circonférence de la base augmente.
Quelle est la mesure de l'angle au centre du secteur représentant la face latérale d'un cône avec un apothème de 5 cm et dont la mesure du rayon de la base est de 3 cm?
Par les propriétés des arcs de cercle, on peut déduire l'égalité suivante :
||mesure de l'angle au centre360∘=mesure de l'arcCirconférencemesure de l'angle au centre360∘=Circonférence de la baseCirconférence du cercle défini par le secteurmesure de l'angle au centre360∘=2π×32π×5mesure de l'angle au centre360∘=\cancel2π×3\cancel2π×5mesure de l'angle au centre360∘=35mesure de l'angle au centre=3×360∘5=216∘||
La construction d'un cône peut être obtenue en dessinant d'abord la base circulaire et en reliant ensuite ses extrémités jusqu'à son apex.
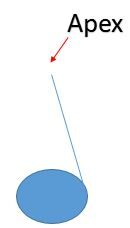
Étape 1 : Représenter la base du cône par un ovale.
Étape 2 : Relier l'extrémité droite d'un diamètre du cercle au sommet du cône (apex).
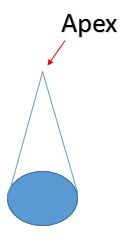
Étape 3 : Relier l'extrémité gauche du même diamètre à l'apex.
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p>La construction d'un cône peut également s'effectuer en procédant à <a href="/fr/eleves/bv/mathematiques/la-rotation-m1406">la rotation</a> d'un triangle autour d'un axe.</p>
</body></html>
Étape 1 : Le triangle de base doit se situer à angle droit par rapport à l'axe de rotation afin de former un cône droit.
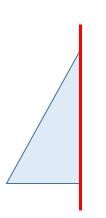
Étape 2 : La rotation de ce triangle de 90o forme un quart de cône.
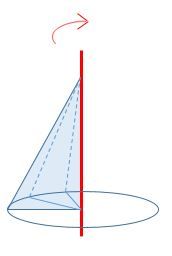
Étape 3 : La rotation de ce triangle de 180o forme un demi-cône.
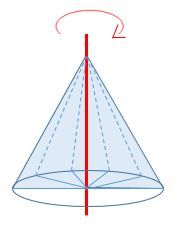
Étape 4 : La rotation de ce triangle de 360o forme un cône complet.
