Une fonction affine est une fonction dont le taux de variation est constant. Sa règle s'écrit sous la forme |f(x) = ax + b| où |a| et |b| sont des nombres réels |(\mathbb{R}).|
Graphiquement, une fonction affine est représentée par une droite.
Les graphiques des droites peuvent varier en fonction de leur taux de variation (paramètre |a|) et de leur ordonnée à l'origine (paramètre |b|). Ainsi, on classe les droites en diverses catégories :
Une fonction polynomiale de degré 0 (de variation nulle) est une fonction qui ne varie pas, c'est-à-dire qu’elle sera toujours égale à un nombre. On dit que des variations de la variable indépendante |(x)| n'entrainent pas de variations de la variable dépendante |(y)|.
L'équation de la fonction polynomiale de degré 0 s'écrit sous la forme suivante.||f(x) = b||où |b| est une constante
Cette règle provient de la règle générale pour les fonctions affines : |f(x) = ax + b.| Toutefois, comme le taux de variation est nul, le paramètre |a| est égal à 0. Ainsi, la règle devient |f(x) = b.|
-
Étant donné que la variable dépendante |(y)| est toujours constante, la table de valeurs d'une fonction de variation nulle est marquée par une valeur constante des |y.|
-
La représentation graphique de cette fonction est une droite parallèle à l'axe des abscisses qui croise l'axe des ordonnées en |(0,b).|
Soit la situation de variation nulle suivante :
Peu importe la variation de la variable |x,| la valeur de |y| est toujours la même, soit |4.|
On peut représenter cette fonction à l'aide de la règle |y=4,| d'une table de valeurs (à gauche ci-dessous) ou d'un graphique (à droite ci-dessous).
| |x| | |y| |
|---|---|
| 5 | 4 |
| 3 | 4 |
| 0 | 4 |
| -2 | 4 |
Une fonction de variation directe (polynomiale de degré 1) est une fonction qui traduit une situation de proportionnalité. Ainsi, des variations constantes de la variable indépendante |(x)| entrainent des variations constantes et non nulles de la variable dépendante |(y).|
L'équation de la fonction polynomiale de degré 1 de variation directe s'écrit sous la forme suivante.||f(x) = ax||où |a\neq 0|
Cette règle provient de la règle générale pour les fonctions affines : |f(x) = ax + b|. Toutefois, comme la situation de variation directe est proportionnelle, l'ordonnée à l'origine |(b)| est nulle car la droite passe par |(0,0).| Ainsi, le paramètre |b| est égal à |0.| Ainsi, la règle devient |f(x) = ax.|
-
La fonction de variation directe passe par le point |(0,0).|
-
La table de valeurs d'une fonction de variation directe est marquée par la présence de la coordonnée |(0,0).|
-
La représentation graphique de cette fonction est une droite oblique qui croise l'axe des ordonnées en |(0,0).|
Soit la situation de variation directe suivante :
Une baignoire, vide au départ, se remplit à raison de 5 litres d'eau par minute. On veut représenter le nombre de litres d'eau dans la baignoire en fonction du temps en minutes.
On peut représenter cette fonction à l'aide de la règle |f(x)=5x| où |x| est le temps en minutes et |f(x)| est le nombre de litres.
On peut aussi la représenter par une table de valeurs (à gauche ci-dessous) ou par un graphique (à droite ci-dessous).
| |x| | |y| |
|---|---|
| 0 | 0 |
| 2 | 10 |
| 4 | 20 |
| 6 | 30 |
Une fonction de variation partielle (polynomiale de degré 1) est une fonction où des variations constantes de la variable indépendante |(x)| entrainent des variations constantes et non nulles de la variable dépendante |(y)|. Toutefois, contrairement à la fonction de variation directe, elle ne traduit pas une situation de proportionnalité puisqu'elle ne passe pas par |(0,0)|.
L'équation de la fonction polynomiale de degré 1 de variation partielle s'écrit sous la forme suivante.
|f(x) = ax + b|
où |a\neq 0| et |b\neq 0|
Cette règle correspond à la règle générale pour les fonctions affines : |f(x) = ax + b.|
On peut aussi écrire l'équation d'une droite sous d'autres formes. Pour en savoir davantage, consultez le lien suivant :
Les formes d'équations d'une droite.
-
La fonction de variation partielle ne passe pas par le point |(0,0).| Elle croise plutôt l'axe des ordonnées au point |(0,b).|
-
La table de valeurs d'une fonction de variation partielle présente une valeur initiale non nulle.
-
La représentation graphique de cette fonction est une droite oblique qui ne passe pas par l'origine du plan cartésien.
Soit la situation de variation partielle suivante.
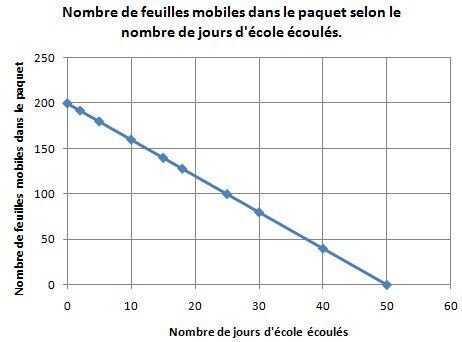
Marc achète un paquet de 200 feuilles mobiles au début de l’année scolaire. Il utilise en moyenne 4 feuilles mobiles par jour d’école. On s’intéresse au nombre de feuilles mobiles qui lui reste dans son paquet selon le nombre de jours d’école écoulés.
On peut représenter cette variation partielle par la règle |f(x) = -4x + 200.|
On peut aussi la représenter par une table de valeurs (à gauche ci-dessous) ou par un graphique (à droite ci-dessous).
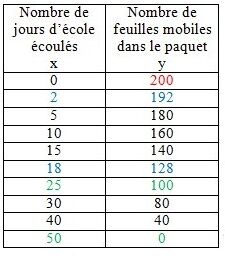
| |\boldsymbol{x:}| Nombre de jours d'école écoulés | |\boldsymbol{f(x):}| Nombre de feuilles mobiles dans le paquet |
|---|---|
| 0 | 200 |
| 2 | 192 |
| 5 | 180 |
| 10 | 160 |
| 15 | 140 |
| 18 | 128 |
| 25 | 100 |
| 30 | 80 |
| 40 | 40 |
| 50 | 0 |