Un solide décomposable est un solide pouvant être séparé en plusieurs solides plus simples.
Lorsqu’on calcule le volume d’un solide décomposable convexe, il est préférable de le décomposer afin d'identifier chacun des solides qui le composent. Par la suite, il suffit de calculer le volume de chacun d'eux à l’aide de leur formule respective et de les additionner.
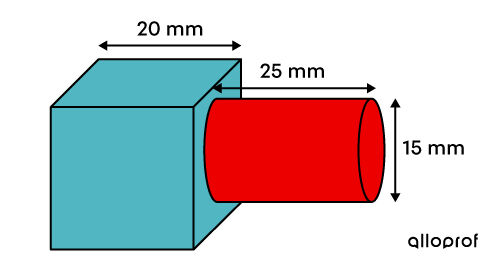
Quel est le volume de ce solide?
-
Identifier la nature des solides
Dans cet exemple, il s'agit d'un cube et d'un cylindre. -
Appliquer les formules ||\begin{align} V &= \color{#51B6C2}{V_\text{cube}} \ +\ \color{#ec0000}{V_\text{cylindre}}\\ &= \color{#51B6C2}{c^3} \quad\ \ + \ \color{#ec0000}{A_b \times h}\\&=\color{#51B6C2}{c^3}\enspace \quad+\ \color{#ec0000}{\pi r^2\times h} \\ &= \color{#51B6C2}{20^3} \quad +\ \ \color{#ec0000}{\pi \left(\dfrac{15}{2}\right)^2 \times 25}\\ &= \color{#51B6C2}{8\ 000}\ + \ \color{#ec0000}{1\ 406{,}25\pi}\\ &\approx 12 \ 417{,}86 \ \text{mm}^3\end{align}||
-
Interpréter la réponse
Le solide a un volume d’environ |12 \ 417{,}86 \ \text{mm}^3.|
Généralement, on utilise l'addition pour calculer le volume des solides décomposables. Par contre, si on veut trouver le volume d'un solide tronqué, on utilise davantage la soustraction.
Pour les solides décomposables non convexes, il faut aussi les décomposer afin d'identifier chacun des solides qui ont été utilisés dans leur construction. Par la suite, on calcule le volume de chacun d'eux à l’aide de leur formule respective. Finalement, on fait une soustraction.
Afin d'innover dans le marché des stylos, un ingénieur décide d'en créer un nouveau de forme cylindrique. À l'intérieur du stylo, il veut intégrer un espace vide en forme de prisme à base carrée afin d’y insérer des cartouches de rechange.
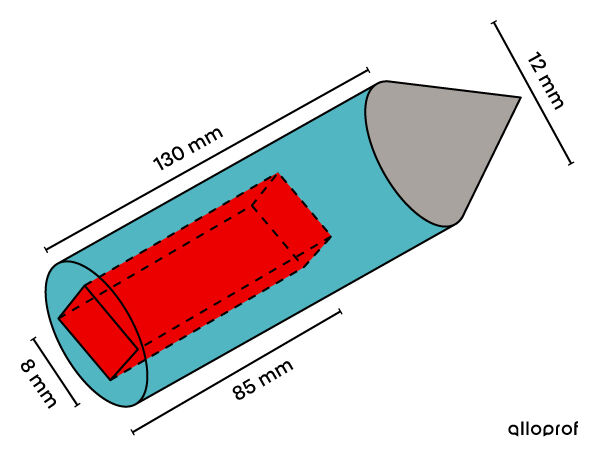
Pour parfaire sa nouvelle création, l'ingénieur veut savoir quel espace est libre à l'intérieur du corps du stylo pour intégrer le reste des composantes.
-
Identifier la nature des solides
Dans le cas présent, il s'agit d'un cylindre et d'un prisme à base carrée. -
Appliquer les formules ||\begin{align} V &= \color{#51B6C2}{V_\text{cylindre}} &&-&&\color{#ec0000}{V_\text{prisme}}\\ &=\color{#51B6C2}{A_b\times h}&&-&&\color{#ec0000}{A_b\times h}\\&= \color{#51B6C2}{\pi r^2 \times h} &&-&&\color{#ec0000}{c^2 \times h}\\ &= \color{#51B6C2}{\pi\left(\dfrac{12}{2}\right)^2 \times 130} &&-&&\color{#ec0000}{8^2 \times85}\\ &= \color{#51B6C2}{4\ 680\pi} &&-&&\color{#ec0000}{5\ 440}\\ &\approx 9 \ 262{,}65 \ \text{mm}^3 \end{align}||
-
Interpréter la réponse
L'espace libre à l'intérieur du corps du stylo est d'environ |9 \ 262{,}65 \ \text{mm}^3.|