Le volume d'un cylindre correspond à l'espace qu'il occupe dans son environnement. Même si ce solide ne fait pas partie de la famille des prismes, la formule pour calculer son volume est la même que celle utilisée pour ces derniers. La seule différence est que l’aire d’une base sera toujours celle d’un disque.
|V = A_b \times h| ou |V=\pi r^2\times h|
où
||\begin{align} V&:\text{Volume}\\A_b &: \text{Aire d'une base}\\ h &: \text{hauteur du cylindre}\\ r &: \text{rayon de la base}\end{align}||
Pour protéger les êtres humains des différentes maladies, les organismes de santé mettent sur pied des programmes de vaccination. Pour donner les vaccins aux gens, ils utilisent ce genre d'équipement.
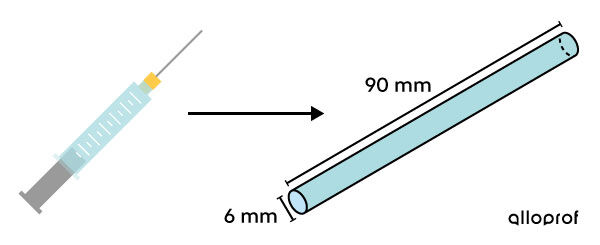
Selon ce modèle, quel volume de médicament maximal, en |\text{mm}^3,| cette seringue peut-elle contenir?
-
Identifier le solide
Selon la forme du dessin, on peut en déduire qu'il s'agit d'un cylindre. -
Appliquer la formule ||\begin{align}V &= A_b \times h\\ \\ &= \pi r^2 \times h \\\\ &= \pi \left(\dfrac{6}{2} \right)^2 \times 90 \\\\ &= \pi(3)^2\times 90 \\\\ &\approx 2\ 544{,}69 \ \text{mm}^3\end{align}||
-
Interpréter la réponse
Selon les données, la seringue peut contenir un maximum d'environ |2\ 544{,}69 \ \text{mm}^3| de médicament.
Remarque : Il faut bien utiliser la mesure du rayon et non la mesure du diamètre.
Dans certains problèmes, il arrive qu’on cherche la mesure de la base ou la hauteur du cylindre alors que le volume est donné. C’est ce qui s’appelle trouver une mesure manquante d'un cylindre à partir du volume. Dans ce cas, la démarche est un peu différente, mais il demeure essentiel de se rappeler la formule du volume associée au cylindre.