A decomposable solid is a solid that can be broken into simpler solids.
When we calculate the volume of a convex decomposable solid, we break it down to identify each of the solids that make up the whole. Next, we calculate the volume of each of the simpler solids using their respective formulas, and then add them together.
What is the volume of the following solid?
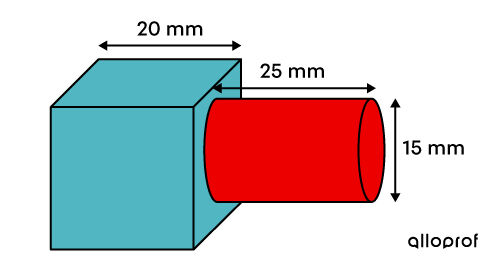
-
Identify the types of solids
The example consists of a cube and a cylinder. -
Apply the formulas
||\begin{align} V &= \color{#51B6C2}{V_\text{cube}} \ +\ \color{#ec0000}{V_\text{cylinder}}\\ &= \color{#51B6C2}{c^3} \quad\ \ + \ \color{#ec0000}{A_b \times h}\\&=\color{#51B6C2}{c^3}\enspace \quad+\ \color{#ec0000}{\pi r^2\times h} \\ &= \color{#51B6C2}{20^3} \quad +\ \ \color{#ec0000}{\pi \left(\dfrac{15}{2}\right)^2 \times 25}\\ &= \color{#51B6C2}{8\ 000}\ + \ \color{#ec0000}{1\ 406.25\pi}\\ &\approx 12 \ 417.86 \ \text{mm}^3\end{align}|| -
Interpret the answer
The solid has a volume of approximately |12 \ 417.86 \ \text{mm}^3.|
Generally, calculating the volume of decomposable solids requires addition. However, subtraction is used more often when finding the volume of a truncated solid.
For non-convex decomposable solids, we break them down to identify the solids used to build them. Next, the volume of each is calculated using their respective formulas. Finally, we subtract the relevant volumes.
To stay innovative in the pen market, an engineer creates a new pen with a cylindrical shape. Inside the pen, an empty space in the form of a square-based prism will be where replacement cartridges are inserted.
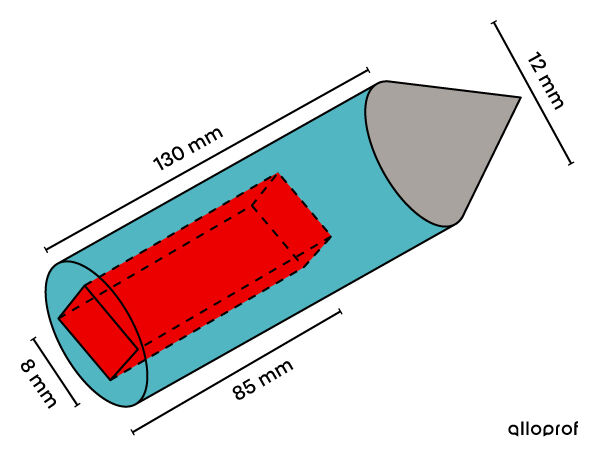
To perfect the new design, the engineer wants to know how much free space inside the pen is available for the rest of the components.
-
Identify the type of solids
In this case, there is a cylinder and a square-based prism. -
Apply the formulas
||\begin{align} V &= \color{#51B6C2}{V_\text{cylinder}} &&-&&\color{#ec0000}{V_\text{prism}}\\ &=\color{#51B6C2}{A_b\times h}&&-&&\color{#ec0000}{A_b\times h}\\&= \color{#51B6C2}{\pi r^2 \times h} &&-&&\color{#ec0000}{c^2 \times h}\\ &= \color{#51B6C2}{\pi\left(\dfrac{12}{2}\right)^2 \times 130} &&-&&\color{#ec0000}{8^2 \times85}\\ &= \color{#51B6C2}{4\ 680\pi} &&-&&\color{#ec0000}{5\ 440}\\ &\approx 9 \ 262.65 \ \text{mm}^3 \end{align}|| -
Interpret the answer
The available space inside the pen is approximately |9 \ 262.65 \ \text{mm}^3.|